이번 포스팅도 이전 포스팅에 이어 Tree 시리즈의 다음인
Binary Search Tree에 대해 설명드리겠습니다.

1. 정의

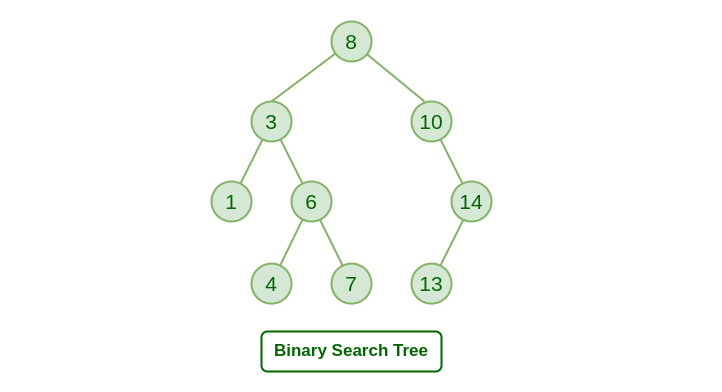
(사진 출처 : geeksforgeeks)

Binary Search Tree는 이진 트리의 한 형태로, 각 노드가 최대 두 개의 자식을 가질 수 있는 구조이며, 데이터의 추가, 삭제, 탐색 등의 연산을 빠르게 수행할 수 있도록 설계되었습니다.

각 노드는 아래의 성질을 만족합니다.
1) 왼쪽 서브 트리에 있는 노드의 키 < 해당 노드의 키
2) 오른쪽 서브 트리에 있는 노드의 키 > 해당 노드의 키
3) 왼쪽 및 오른쪽 서브 트리 또한 Binary Search Tree

이 성질 덕분에 Binary Search Tree는 데이터의 추가, 삭제, 탐색 작업을 로그 시간 복잡도에서 수행할 수 있습니다.

2. 연산

1) 탐색(Search)

탐색하려는 키를 루트 노드의 키와 비교하여, 키가 루트 노드의 키보다 작으면 왼쪽 서브 트리에서 탐색을 계속하고, 크면 오른쪽 서브 트리에서 탐색을 계속합니다.
서브 트리가 없을 때까지 혹은 찾고자 하는 키를 가진 노드를 찾을 때까지 반복합니다.

class Node:
    def __init__(self, key):
        self.left = None
        self.right = None
        self.val = key

def search(root, key):
    # 루트가 None이거나 key가 루트의 값과 같은 경우
    if root is None or root.val == key:
        return root

    # key가 루트의 값보다 작다면 왼쪽 서브트리에서 재귀적으로 탐색
    if root.val > key:
        return search(root.left, key)

    # key가 루트의 값보다 크다면 오른쪽 서브트리에서 재귀적으로 탐색
    return search(root.right, key)

2) 삽입(Insertion)

새로운 키를 탐색할 땐 적절한 위치를 찾습니다. 루트 노트부터 시작하여 삽입하려는 키가 현재 노드의 키보다 작으면 왼쪽으로, 크면 오른쪽으로 이동합니다.
더 이상 자식 노드가 없는 위치에 새 노드를 추가합니다.

def insert(root, key):
    # 트리가 비어있으면 새 노드를 생성
    if root is None:
        return Node(key)

    # 그렇지 않으면 재귀적으로 트리를 내려감
    if key < root.val:
        root.left = insert(root.left, key)
    else:
        root.right = insert(root.right, key)

    return root

3) 삭제(Deletion)

삭제는 조금 복잡합니다. 경우의 수가 세 개로 나뉩니다.

• 삭제하려는 노드에 자식이 없다면 그냥 해당 노드를 제거
• 자식이 하나인 경우에는 해당 노드를 제거하고 그 자리를 자식 노드가 차지
• 삭제하려는 노드에 두 개의 자식이 있는 경우로, 보통 삭제하려는 노드의 오른쪽 서브 트리에서 가장 작은 값을 가진 노드, 또는 가장 큰 값을 가진 노드로 대체

def delete(root, key):
    # 기본 경우: 루트가 None이면
    if root is None:
        return root

    # 삭제할 키가 루트보다 작으면 왼쪽 서브트리에서 삭제
    if key < root.val:
        root.left = delete(root.left, key)

    # 삭제할 키가 루트보다 크면 오른쪽 서브트리에서 삭제
    elif key > root.val:
        root.right = delete(root.right, key)

    # 루트가 삭제할 노드일 때
    else:
        # 노드에 하나의 자식만 있거나 자식이 없는 경우
        if root.left is None:
            temp = root.right
            root = None
            return temp

        elif root.right is None:
            temp = root.left
            root = None
            return temp

        # 두 자식이 있는 경우: 후계 노드(오른쪽 서브트리의 최소값)를 찾음
        temp = minValueNode(root.right)

        # 후계 노드의 값을 현재 노드에 복사
        root.val = temp.val

        # 후계 노드 삭제
        root.right = delete(root.right, temp.val)

    return root

def minValueNode(node):
    current = node
    # 가장 왼쪽 노드를 찾아 최소값을 찾음
    while(current.left is not None):
        current = current.left
    return current

3. 장점 및 단점

1) 장점

• 평균적으로 탐색, 삽입, 삭제 작업을 빠르게 수행 가능
• 정렬된 데이터를 유지하면서도 동적인 데이터 집합 관리를 할 수 있음

2) 단점

• 최악의 경우(트리가 한쪽으로만 치우쳐 있는 경우) 모든 연산이 O(n)시간이 걸릴 수 있음
• 데이터가 미리 정렬되어 있을 경우 불균형한 트리가 될 가능성이 높아지므로, 이를 방지하기 위해 균형을 잡는 알고리즘(예: AVL 트리, 레드-블랙 트리)을 적용 가능

이진 탐색 트리의 삭제는 개념도 어려운데 코드 구현도 다소 까다로운 면이 있는 것 같습니다...
그래도 공부는 해야하니까..... 화이팅합시다

그럼 안뇽