Binary Tree

이번 포스팅에는 트리의 종류 중 하나인 Binary Tree(이진 트리)에 대해 조금 더 자세히 알아보는 시간을 갖도록하겠습니다.

Binary Tree의 종류는 총 여섯가지가 있는데요,
이에 대해 차근차근 설명하겠습니다.

1. Full Binary Tree

Full Binary Tree는 모든 레벨이 완전히 채워져 있으며, 마지막 레벨을 제외한 모든 레벨에서 노드가 최대로 존재합니다.
마지막 레벨의 노드는 왼쪽부터 오른쪽으로 채워져있습니다.

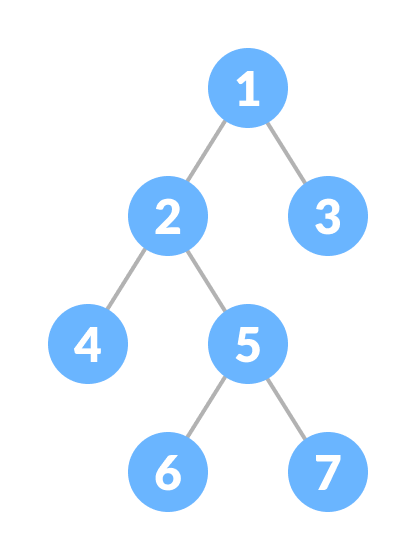
class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

def create_full_binary_tree():
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)
    return root

2. Perfect Binary Tree

Perfect Binary Tree는 모든 레벨이 노트로 완전히 채워져 있고, 모든 리프 노드가 동일한 깊이를 가지는 Binary Tree입니다.
이 구조는 데이터를 효율적으로 관리할 수 있도록 해줍니다.

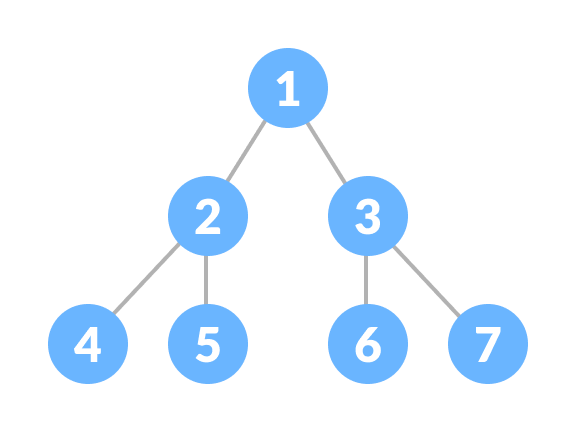
def create_perfect_binary_tree():
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)
    root.right.left = TreeNode(6)
    root.right.right = TreeNode(7)
    return root

3. Complete Binary Tree

Complete Binary Tree는 모든 레벨이 왼쪽부터 차례대로 채워져 있으며, 마지막 레벨은 왼쪽부터 채워집니다. 이 구조는 heap과 같은 데이터 구조를 구현할 때 유용합니다.

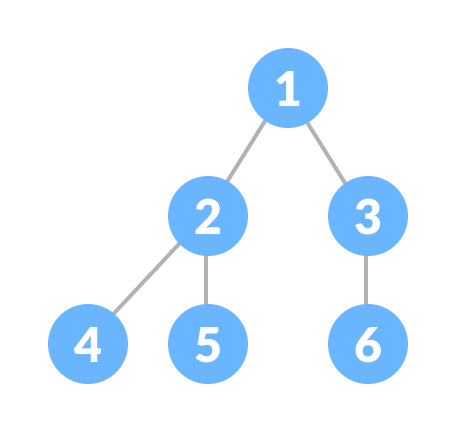
def create_complete_binary_tree():
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)
    return root

4. Degenerate or Pathological Tree

egenerate or Pathological Tree는 각 노드가 하나의 자식만을 가지는 이진 트리로, 사실상 Linked List와 유사합니다. 이 구조는 트리의 이점을 제공하지 않으며, 검색과 같은 작업에서 비효율적일 수 있습니다.

def create_degenerate_tree():
    root = TreeNode(1)
    root.right = TreeNode(2)
    root.right.right = TreeNode(3)
    root.right.right.right = TreeNode(4)
    return root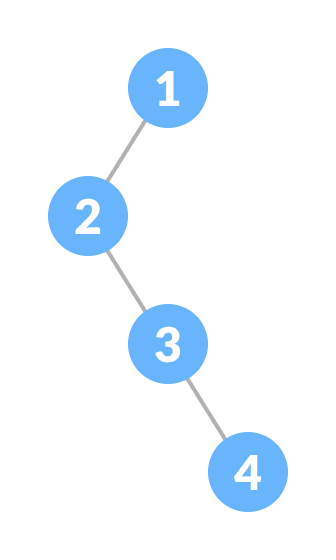

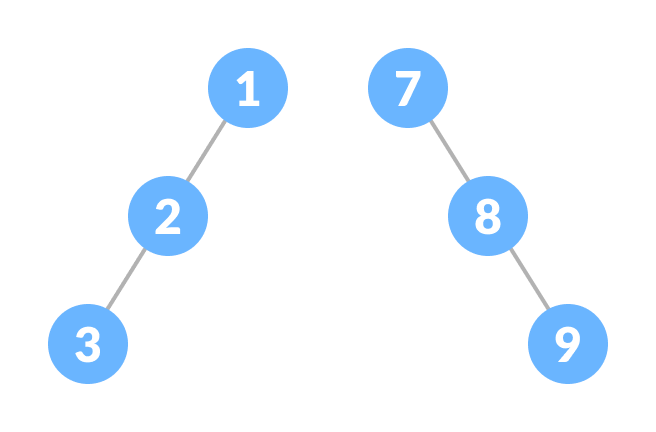
5. Skewed Binary Tree

Skewed Binary Tree는 모든 노드가 하나의 방향으로만 자식을 가지는 이진 트리입니다. 왼쪽 편향 트리는 모든 노드가 왼쪽 자식만을 가지고, 오른쪽 편향 트리는 모든 노드가 오른쪽 자식만을 가집니다.

def create_right_skewed_tree():
    root = TreeNode(1)
    root.right = TreeNode(2)
    root.right.right = TreeNode(3)
    return root

6. Balanced Binary Tre

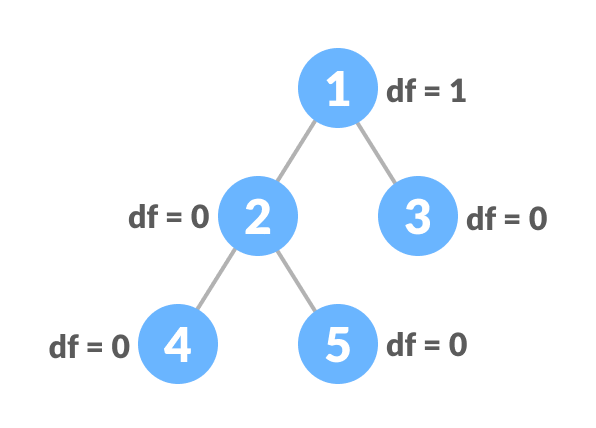
균형 이진 트리는 모든 노드에서 왼쪽 부분 트리와 오른쪽 부분 트리의 높이 차이가 1 이하인 트리입니다.
이 구조는 검색, 삽입, 삭제 작업을 빠르게 수행할 수 있도록 도와줍니다.

def create_balanced_binary_tree():
    root = TreeNode(1)
    root.left = TreeNode(2)
    root.right = TreeNode(3)
    root.left.left = TreeNode(4)
    root.left.right = TreeNode(5)
    root.right.left = TreeNode(6)
    return root

다소 헷갈릴 것 같아 Full Binary Tree, Perfect Binary Tree, Complete Binary Tree의 차이점에 대해 설명드리고 포스팅 마치도록하겠습니다.

Perfect Binary Tree : 어떤 레벨도 누락된 노드가 없어야 함
Full Binary Tree : 모든 내부 노드가 0개 또는 2개의 자식을 가지는 이진 트리
Complete Binary Tree : 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져있으며, 마지막 레벨의 노드는 왼쪽에서 오른쪽으로 차례대로 채워짐.

그럼 안뇽