[알고리즘] 동적 프로그래밍 (Dynamic Programming, DP)

동적 프로그래밍 (Dynamic Programming, 이하 DP) 에 대해서 알아보도록 하자.
DP는, 작은 문제를 통해 큰 문제를 해결해나가는 기법이다. 여기서 의문이 들 수 있다. 나중에 포스팅 할 내용이지만, '분할 정복'도 작은 문제를 통해 큰 문제를 해결해나가는 기법이다.
그렇다면, DP와 분할 정복의 공통점과 차이점이 무엇일까?

공통점

• 큰 문제를 작은 문제로 쪼개어 풀이한 후, 큰 문제에 대한 해답을 도출

차이점

• DP : '메모이제이션' 기법을 사용

• DP : 겹치는 부분문제가 발생

• DP : 상향식(Bottom-Up) 접근

• 분할정복 : '메모이제이션' 기법 사용 안함

• 분할정복 : 겹치는 부분문제가 발생하지 않음

• 분할정복 : 하향식(Top-Down) 접근

예시

동적 프로그래밍의 예시를 들어보자. 분할정복의 예시에 대해서는 이후에 포스팅을 하고, 링크를 추가하도록 한다. 동적 프로그래밍의 예시로는 피보나치 수열이 대표적이다. 피보나치 수열은 다음과 같은 수열이다.

F(n) = F(n-2) + F(n-1), n은 양수
F(0) = 1
F(1) = 1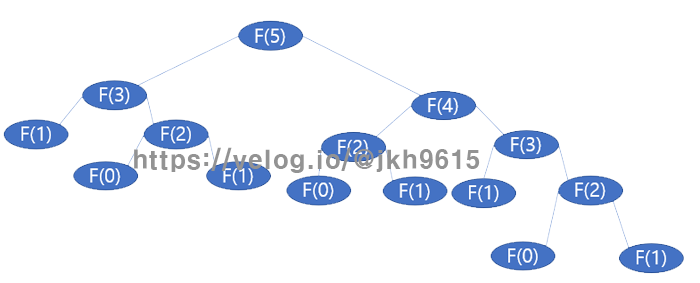

위 그림은 F(5)를 구하기 위해 재귀방식으로 접근한 트리이다.
F(5) = F(3) + F(4)
에서 다시
F(3) = F(1) + F(2)
F(4) = F(2) + F(3)
에서 다시
F(2) = F(0) + F(1)
F(2) = F(0) + F(1)
F(3) = F(1) + F(2)
.....
F(5)를 구하기 위해 계산되는 수식이 너무 많다. 재귀로 작성시 코드는 간단하지만 엄청난 자원 소모가 생긴다. F(5)를 구하니 이정도이지, F(100)을 구하는 순간... 답도 없다. 이를 동적 프로그래밍으로 접근해보자.
int 배열을 만들어주자.

int[] dp = new int[6]; // dp[5]까지 구해본다.

dp[0] = 0;
dp[1] = 1;
dp[2] = dp[0] + dp[1]; // 0+1 = 1
dp[3] = dp[1] + dp[2]; // 1+1 = 2
dp[4] = dp[2] + dp[3]; // 1+2 = 3
dp[5] = dp[3] + dp[4]; // 2+3 = 5

굉장히 간단하게 구해진다.

위에 '차이점'에서,
1. 메모이제이션 사용 > 배열을 만들어서 각 피보나치 값을 저장했다.
2. 겹치는 부분문제 발생 > 재귀함수 트리 이미지를 보면, F(2)를 여러번 구하는 장면이다.
3. 상향식 접근 > 트리에서 가장 낮은 F(0), F(1)부터 시작하여 F(5)를 구했다.
이 사용된 것을 볼 수 있다.

예시 문제 : 백준 2748, 피보나치 수 2
주의할 점 : 피보나치 수가 int범위를 넘어갈 수 있음에 주의한다!
정답 (자바코드) : 먼저 풀어본 후, 스크롤을 아래로 내린다.

import java.util.Scanner;
public class Main {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		long[] dp = new long[n+1];
		if(n == 1) {
			System.out.println(1);
			return;
		}
		dp[0] = 0;
		dp[1] = 1;
		for(int i = 2; i <= n; i++) {
			dp[i] = dp[i-1] + dp[i-2];
		}
		System.out.println(dp[n]);
	}
}