[알고리즘] 백준 15993 1, 2, 3 더하기 (8) Java

문제 정보

플랫폼 : 백준
분류 : Dynamic Programming (동적 프로그래밍)
난이도 : 실버1
링크 : https://www.acmicpc.net/problem/15993

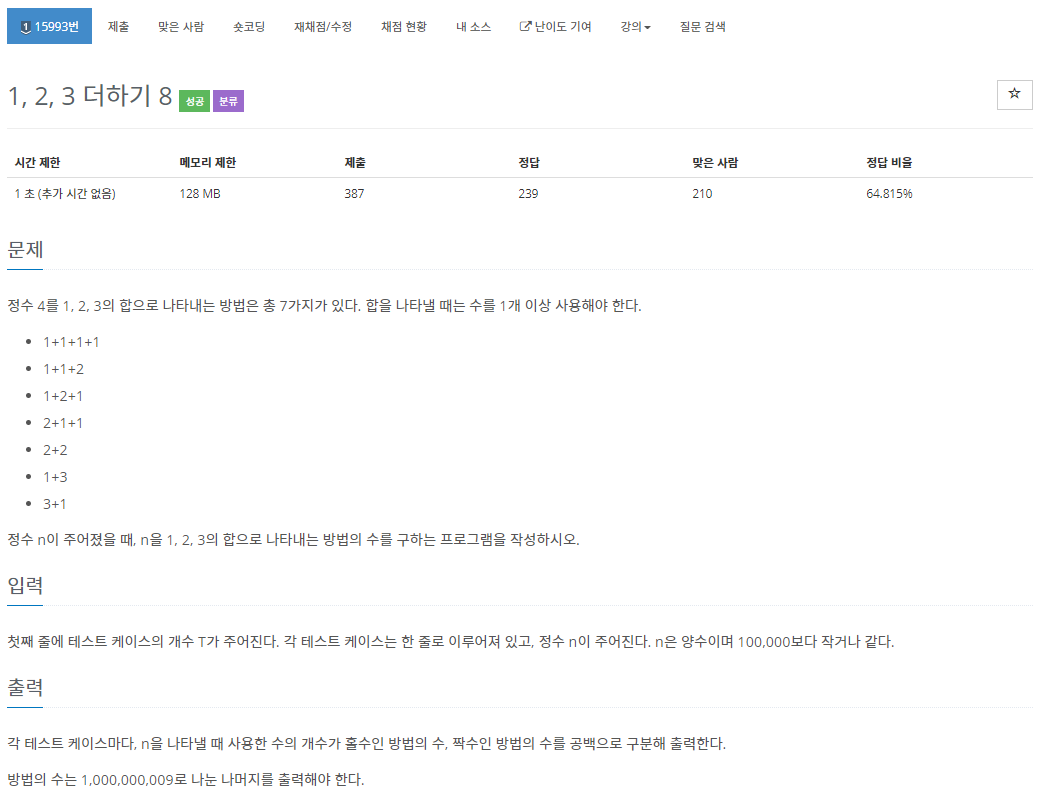
시간제한 및 메모리 제한 검증

O(n) 풀이 : 시간제한 ok
자료형 : 최대 30억, long

풀이

주말동안 Dynamic Programming 유형인 [1, 2, 3 더하기] 시리즈의 문제를 풀어봤다.

만약, 이전 1, 2, 3 더하기 시리즈를 풀지 않았거나, 풀이를 보지 않았다면 이곳을 클릭하여 이전 풀이를 먼저 보고오자!

점화식
dp[i][0] = (dp[i-1][1] + dp[i-2][1] + dp[i-3][1]) % 1_000_000_009;
dp[i][1] = (dp[i-1][0] + dp[i-2][0] + dp[i-3][0]) % 1_000_000_009;
(n >= 4)

이 문제는 이전 문제인 1, 2, 3 더하기 (7)의 풀이를 동일하게 이용해, 짝수개의 합과 홀수개의 합을 출력하려고 했다. 그러나 메모리 초과가 났다. 이유는 당연히... n*n size의 배열을 만드는데, n = 100,000이므로 배열의 크기가 100,000,000,000 (1천억)개가 만들어졌기 때문..... 하는 수 없이 다른 풀이를 생각해야했다.
dp[n+1][2]를 정의했고,

dp[i][0]은 숫자 i의 짝수개 수식의 수
dp[i][1]은 숫자 i의 홀수개 수식의 수
라고 정의했다.

점화식은,
홀수개의 수식을 가진 i-1, i-2, i-3에서 각각 +1, +2, +3을 하면 i의 짝수개가 되고, (홀수 + 1 = 짝수)
짝수개의 수식을 가진 i-1, i-2, i-3에서 각각 +1, +2, +3을 하면 i의 홀수개가 된다 (짝수 + 1 = 홀수)는 의미이다.

위와 같은 과정을 통해
dp[i][0] = (dp[i-1][1] + dp[i-2][1] + dp[i-3][1]) % 1_000_000_009;
dp[i][1] = (dp[i-1][0] + dp[i-2][0] + dp[i-3][0]) % 1_000_000_009;
(n >= 4)라는 점화식이 나온다.

모듈러가 나오는 이유는, 10억9로 나누어 출력하라는 제한사항이 있기 때문이다. 마지막에 모듈러를 넣는 것이 아니라, 계산 과정 중간에 모듈러를 넣는 이유는 이곳을 참조하자.

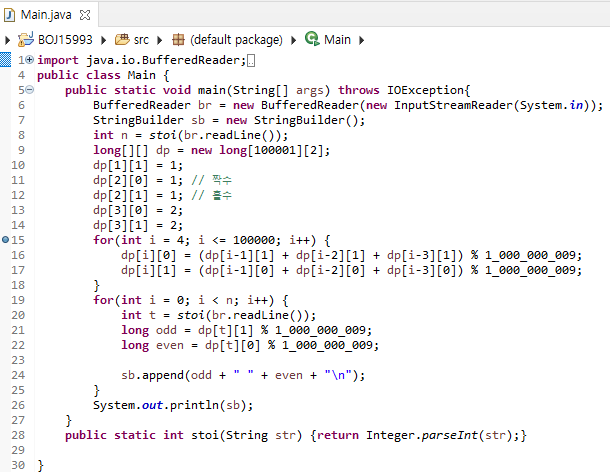
코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
	public static void main(String[] args) throws IOException{
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();
		int n = stoi(br.readLine());
		long[][] dp = new long[100001][2];
		dp[1][1] = 1;
		dp[2][0] = 1; // 짝수
		dp[2][1] = 1; // 홀수
		dp[3][0] = 2;
		dp[3][1] = 2;
		for(int i = 4; i <= 100000; i++) {
			dp[i][0] = (dp[i-1][1] + dp[i-2][1] + dp[i-3][1]) % 1_000_000_009;
			dp[i][1] = (dp[i-1][0] + dp[i-2][0] + dp[i-3][0]) % 1_000_000_009;
		}
		for(int i = 0; i < n; i++) {
			int t = stoi(br.readLine());
			long odd = dp[t][1] % 1_000_000_009;
			long even = dp[t][0] % 1_000_000_009;
			
			sb.append(odd + " " + even + "\n");
		}
		System.out.println(sb);
	}
	public static int stoi(String str) {return Integer.parseInt(str);}

}

더 많은 정답 코드

블로그를 쓰기 이전에 풀어본 문제들이 많다. 해설강의는 없지만, 백준 문제의 풀이 코드가 필요한 경우 이곳을 클릭하여 소스코드를 참조해보도록 하자. 단, 코드만 복사-붙여넣기 하는것은 본인에게 결코 도움이 되지 않는다. 반드시 먼저 생각해보고, 막히는 경우에 참고하고 왜 이렇게 코드가 작성됐는지를 다시 한 번 생각해보는 습관을 들이자.