
문제 정보
플랫폼 : 백준
분류 : Dynamic Programming (동적 프로그래밍)
난이도 : 실버1
링크 : https://www.acmicpc.net/problem/16195
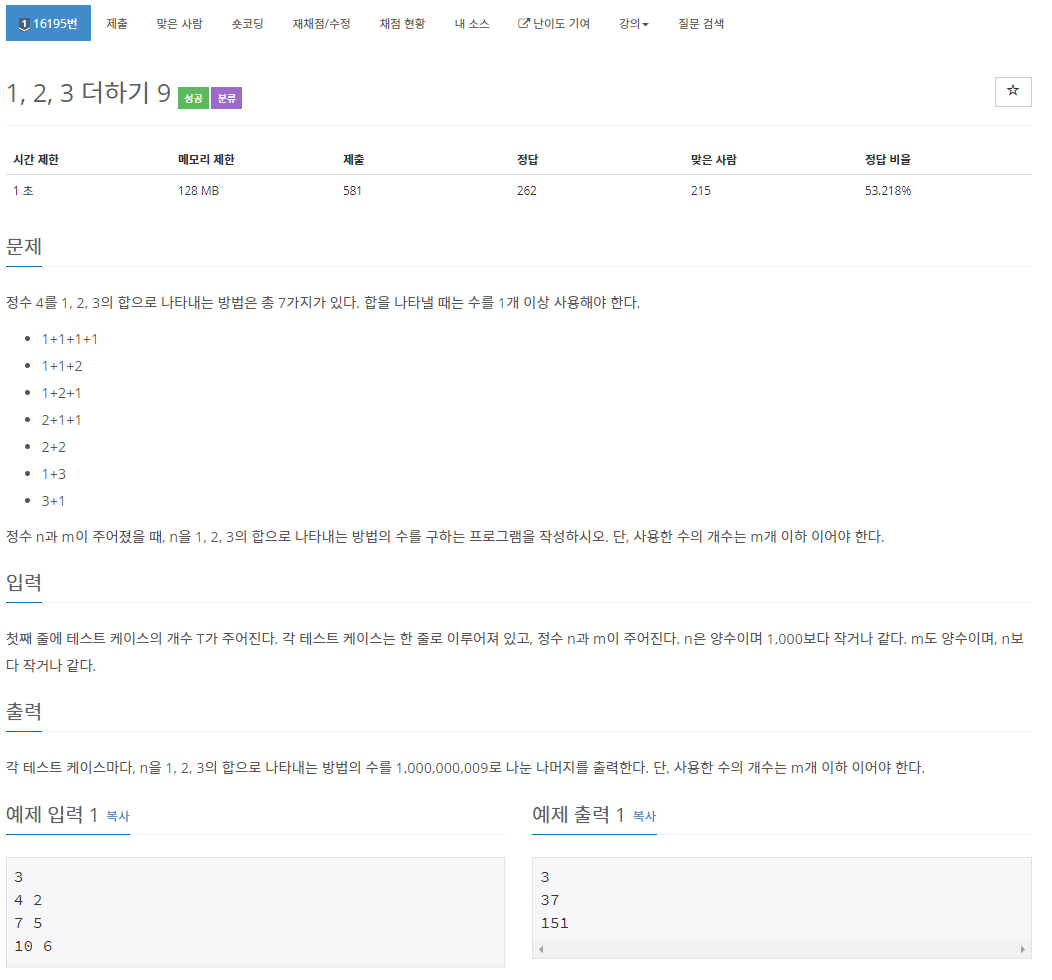
시간제한 및 메모리 제한 검증
O(n^2) 풀이 : 시간제한 ok (1000*1000 = 100만이므로, 이론상 0.01초)
자료형 : 최대 30억, long
풀이
(이 문제는 1, 2, 3 더하기(7)의 응용문제이다! (그래서 복붙했다.) 이 문제를 풀기 전에 1, 2, 3더하기 (7)을 보고오면 더욱 수월하다!
주말동안 Dynamic Programming 유형인 [1, 2, 3 더하기] 시리즈의 문제를 풀어봤다.
만약, 이전 1, 2, 3 더하기 시리즈를 풀지 않았거나, 풀이를 보지 않았다면 이곳을 클릭하여 이전 풀이를 먼저 보고오자!
점화식
dp[i][j] = (dp[i-1][j-1] + dp[i-2][j-1] + dp[i-3][j-1]) % 1_000_000_009 (n >= 4)
이 문제는 2차원 배열을 사용하지만, 이전에 사용하던 2차원 배열과는 사뭇 다른 느낌이다. 이전에 사용하던
dp[i][j] = 임의의 수 i의 수식이 j로 끝나는 경우 였다면,
이번에 사용하는 dp[i][j] = 임의의 수 i를 j개의 수식으로 표현하는 방법이다.
뭐 대충 어떤 말이냐면..

이런거다.
dp는 n+1*n+1만큼의 사이즈가 필요하다. dp[n+1][n+1] 에서 색칠된 부분은 1이 n개 모여서 만들어질 수 있기 때문이다.
5를 만들어보자.

위와 같은 경우의 수가 있을 것이다. 이를 표로 나타내보자
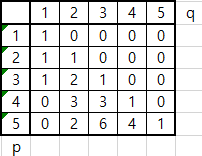
p를 만들기 위해, q개만큼 사용된 수식이 표와 같다는 말이다.
즉, 1을 만들기 위해 1개의 수식이 1번
2를 만들기 위해 1개의 수식이 1번, 2개의 수식이 1번
3을 만들기 위해 1개의 수식이 1번, 2개의 수식이 2번, 3개의 수식이 3번
...사용됐다는 말이다. 여기서 규칙성을 찾을 수 있다.
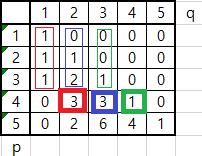
빨간색 굵은 네모를 구하기 위해 빨간색 얇은 네모의 합이,
파란색 굵은 네모를 구하기 위해 파란색 얇은 네모의 합이,
초록색 굵은 네모를 구하기 위해 초록색 얇은 네모의 합이 사용됐다.
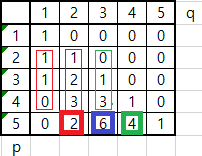
위 사진도 이와 같이 구할 수 있다.
위 사진이 말하는 바는,
[5를 2개의 수식으로 만드는 경우의 수]
- 2를 1개만 사용하는 경우에다가 +3 을 하여 2개의 수식으로 5를 만든다.
- 3을 1개만 사용하는 경우에다가 +2 을 하여 2개의 수식으로 5를 만든다.
[5를 3개의 수식으로 만드는 경우의 수]
- 2개의 수식으로 2를 만드는 경우에다가 +3 을 하여 3개의 수식으로 5를 만든다.
- 2개의 수식으로 3을 만드는 경우에다가 +2 을 하여 3개의 수식으로 5를 만든다.
- 2개의 수식으로 4를 만드는 경우에다가 +1 을 하여 3개의 수식으로 5를 만든다.
...
위와 같은 과정을 통해
dp[i][j] = (dp[i-1][j-1] + dp[i-2][j-1] + dp[i-3][j-1]) % 1_000_000_009 (n >= 4)라는 점화식이 나온다.
모듈러가 나오는 이유는, 10억9로 나누어 출력하라는 제한사항이 있기 때문이다. 마지막에 모듈러를 넣는 것이 아니라, 계산 과정 중간에 모듈러를 넣는 이유는 이곳을 참조하자.
그러나! 이 문제는 1, 2, 3더하기 (7)과는 다르게, m 개 이하의 수식으로 사용된 개수를 구해야한다.
따라서, dp[i][1] ~ dp[i][m]까지의 합을 출력하면 된다.
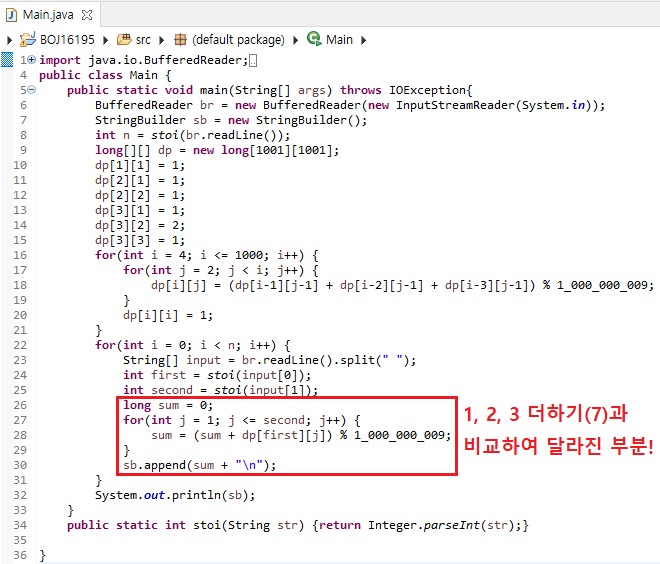
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int n = stoi(br.readLine());
long[][] dp = new long[1001][1001];
dp[1][1] = 1;
dp[2][1] = 1;
dp[2][2] = 1;
dp[3][1] = 1;
dp[3][2] = 2;
dp[3][3] = 1;
for(int i = 4; i <= 1000; i++) {
for(int j = 2; j < i; j++) {
dp[i][j] = (dp[i-1][j-1] + dp[i-2][j-1] + dp[i-3][j-1]) % 1_000_000_009;
}
dp[i][i] = 1;
}
for(int i = 0; i < n; i++) {
String[] input = br.readLine().split(" ");
int first = stoi(input[0]);
int second = stoi(input[1]);
long sum = 0;
for(int j = 1; j <= second; j++) {
sum = (sum + dp[first][j]) % 1_000_000_009;
}
sb.append(sum + "\n");
}
System.out.println(sb);
}
public static int stoi(String str) {return Integer.parseInt(str);}
}
더 많은 정답 코드
블로그를 쓰기 이전에 풀어본 문제들이 많다. 해설강의는 없지만, 백준 문제의 풀이 코드가 필요한 경우 이곳을 클릭하여 소스코드를 참조해보도록 하자. 단, 코드만 복사-붙여넣기 하는것은 본인에게 결코 도움이 되지 않는다. 반드시 먼저 생각해보고, 막히는 경우에 참고하고 왜 이렇게 코드가 작성됐는지를 다시 한 번 생각해보는 습관을 들이자.
