K Nearest Neighbor
Test 데이터와 가까운 k개의 Train 데이터의 y값을 비교
분류와 회귀 문제를 모두 다룰 수 있음.
- 분류: class 다수결로 결과 class 예측
- 회귀: 평균값으로 결과값 예측 (정확도 떨어짐)
비모수 적인 방식(통계적 방식 아님)
구체적인 데이터를 가지고 예측을 요청할 때 k개의 가장 가까운 사례를 Train data set에서 찾아 해당하는 데이터의 y값을 기반으로 예측 결과 제시
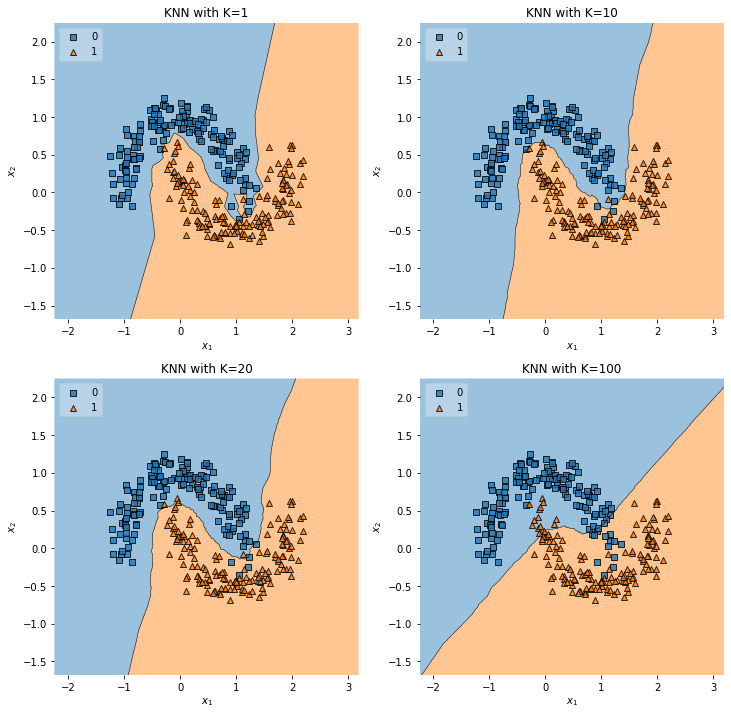
동점을 막기 위해 k값은 대개 홀수로 정한다.
분류
객체는 K개의 최근접 이웃 사이에서 가장 공통적인 항목에 할당되는 객체로 과반수 의결에 의해 분류
k가 너무 작으면 오버피팅
회귀
K개의 최근접 이웃을 찾고 해당 이웃이 가지고 있는 값의 평균이 OUTPUT값이 됨
거리 기준
민코프스키 거리;
유클리디안 거리와 맨해탄 거리의 일반화 형태
맨하탄 거리: |x-x'| + |y-y'|
거리 개념을 사용하면 Normalization 사용 검토
폭이 너무 좁으면 잘못된 결과 낼 수 있음. x와 y축에 대해서 정규화를 통해 늘려줘야 할 필요 있음
장점
단순함
데이터에 대한 기본 가정이 없어서 비선형 데이터에 유용
분류와 회귀 모두에 사용 가능하고 이상값 찾기에도 사용
대체로 우수한 결과
단점
계산비용 높음
데이터 많을 수록 계산 속도 느려지고 데이터의 지역구조에 민감
최적의 K값 찾기 쉽지 않음 (K값 낮으면 over, 높으면 underfitting)
