생각 흐름
- dp 문제집에서 봤으므로 이것은 dp로 푸는 문제일 것이다.
- dp인 것을 몰랐다면 막연히 정렬한 다음 순차적으로 합치게 했을 것이다. (크기가 작은 파일이 병합에 참여하는 횟수를 늘리도록)
- 하지만, 이 항상 비용을 작게 만든다고 보장할 수 없다. 예를 들어 가 보다 크기 때문이다.
- 따라서 이 문제를 해결할 수 있는 하나로 정리될 수 있는 그리디한 방법이 없다. -> 모든 에 대해서 부터 까지의 최소 합을 구해야 한다.
- 이때 반복되는 작업을 최소화하기 위해 메모이제이션을 사용한다. 이것이 없다면, 일례로 3부터 7까지와 3부터 10까지의 최소합을 구할 때 3부터 5까지의 합을 구하는 과정이 반복될 수 있다.
풀이
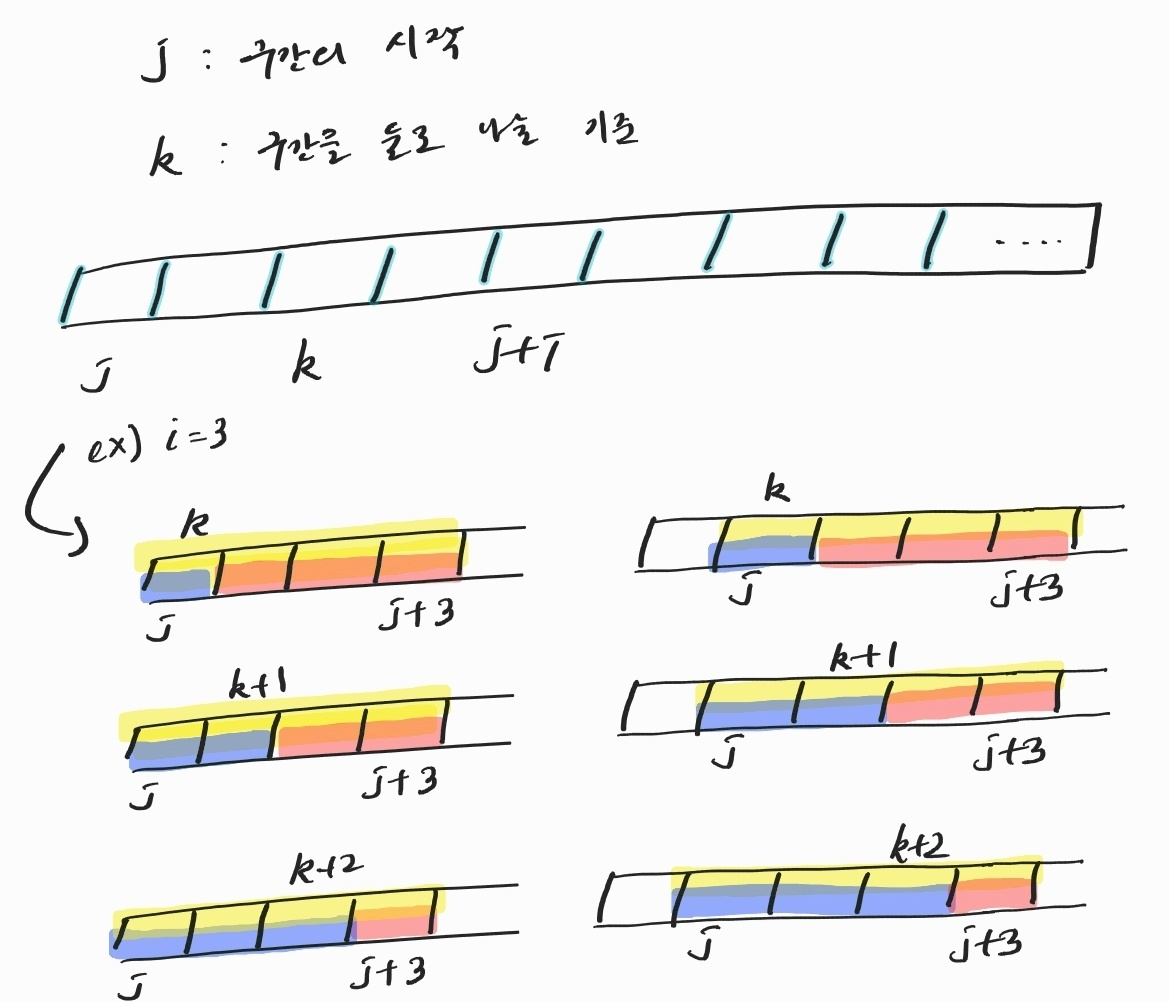
구간을 [시작, 시작 + 크기]라고 하자.
시작은 0부터 시작한다.
크기를 1부터 구간의 마지막 인덱스가 K-1가 될 때까지 넓혀간다.
구간을 둘로 나누는 기준을 구간의 시작부터 구간의 마지막 바로 직전까지 이동해간다.
이렇게 하면 모든 시작점에서 시작하는 구간을 모든 기준으로 나눈 두 부분의 파일을 합하는 최소합을 모든 구간 크기에 대해 구할 수 있다.
어떤 구간에 대해서 그 구간의 파일을 합치는 데 드는 최소 비용은
시작~기준, 기준+1~시작+크기 중 작은 값 (왼쪽과 오른쪽)에 해당 구간합을 더한 값이다.
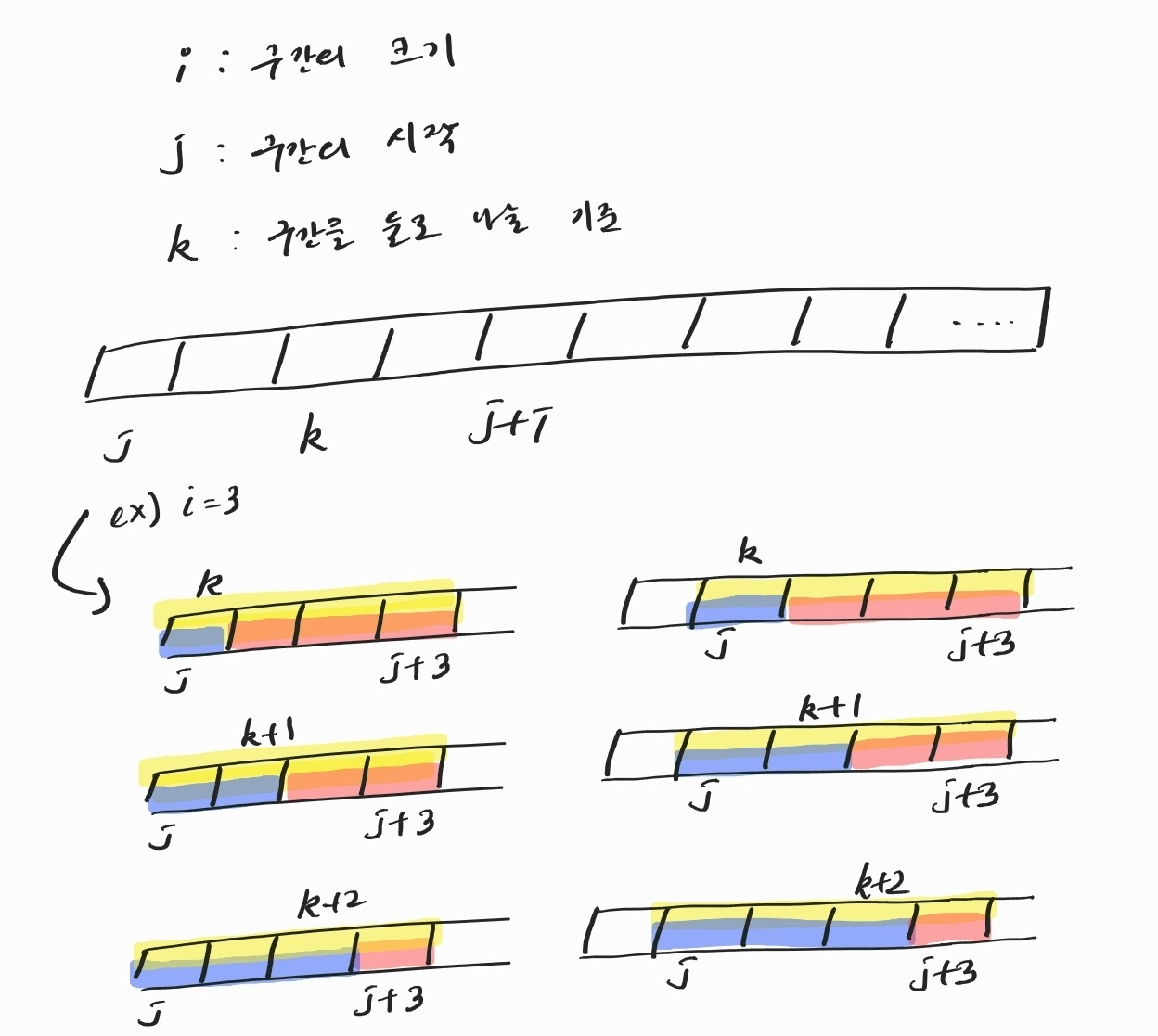
- 구간을 나누는 기준을 j부터 j+i-1까지 이동한다.
- 구간의 시작점을 이동시킨다.
- 구간의 크기를 늘린다.
※구간의 크기를 가장 나중에 늘리는 이유
dp가 필요없는 부분부터 시작해서 스노우 볼을 굴리기 위함.
파일 두 개를 합치는 것은 둘의 합이기 때문에 dp값이 필요가 없음.
각각의 부분에 대해서 최소값을 구한다면 (왼쪽 부분합 + 오른쪽 부분합) 그 구간의 부분합을 더해주면 된다. (둘을 합칠 때 발생하는 비용)
이 문제를 통해서 dp 알고리즘을 쓸 때 다음의 순서대로 설계를 해야한다는 것을 알았다.
- 완전탐색을 한다고 했을 때, 그 하나의 시행을 개의 수로 표현할 수 있는 방법을 찾는다.
- dp배열이 필요 없이 시작할 수 있을 때가 언제인지 먼저 알아본다. 이때는 문제에서 준 값으로만 구할 수 있는 초기값들이다.
- 그 초기값을 이용해 발전시켜 점점 dp값을 이용할 수 있는 방향을 생각해본다.
코드
import math
import sys
scan = sys.stdin.readline
def solution():
T = int(scan())
for t in range(T):
tc()
def tc():
K, arr = get_input()
sums = get_sums(K, arr)
dp = [[0 for _ in range(K)] for _ in range(K)]
for i in range(1, K):
for j in range(K - i):
dp[j][j + i] = math.inf
for k in range(j, j + i):
dp[j][j + i] = min(dp[j][j + i], dp[j][k] + dp[k+1][j + i])
dp[j][j + i] += (sums[j + i] - sums[j] + arr[j])
sys.stdout.write("%d\n" % dp[0][K-1])
def get_input():
K = int(scan())
arr = list(map(int, scan().split()))
return K, arr
def get_sums(K, arr):
sums = [0 for _ in range(K)]
sums[0] = arr[0]
for i in range(1, K):
sums[i] = sums[i-1] + arr[i]
return sums
solution()