확률 분포

Kyojun Jin·2024년 4월 4일

Data Science

목록 보기

3/14

확률 변수

표본공간의 원소를 실수로 대응한 값
확률적인 과정(무작위 실험)의 결과를 수치적으로 표현하는 변수

예) 동전을 5번 던졌을 때 앞면이 x번 나올 확률 (이는 이항 분포를 따른다.)

확률 분포: 확률 변수와 그 값이 나올 수 있는 확률로 대응시켜 표시하는 것

이산확률분포의 기대값, 분산

$E(a) = a \\E(bX) = bE(X) \\E(a + bX) = a + bE(X) \\ E(X + Y) = E(X) + E(Y) \\ E(aX + bY) = aE(X) + bE(Y)$

$V(a) = 0 \\V(a + X) = V(X) \\ V(bX) = b^2V(X) \\$ $V(X + Y) = V(X) + V(Y)$ (독립일 때)
$V(X + Y) = V(X) + V(Y) + 2Cov(X, Y)$ (독립 아닐 때)

확률 함수

확률 변수의 특성에 따라서 확률 질량 함수(이산), 확률 밀도 함수(연속)로 나뉜다.

확률 질량 함수

이산 확률 변수에서 특정 값에 대한 확률을 나타냄.

베르누이 분포

어떤 시행을 해서 어떤 일이 일어나거나 안 일어나거나에 대한 분포. (동전 던지기, 주사위에서 3이 나오거나 안 나오거나)

확률 = $p$
기대값 = $p$
분산 = $pq \ (\because q = 1-p)$

이항 분포

연속 n번 해서 k번 성공할 확률에 대한 분포를 함수로 표현. n이 1이면 베르누이 분포

시행 횟수 n이 엄청 크거나 성공확률이 0.5에 가까우면 좌우대칭 종모양이다.

p가 1/2보다 작고 n이 작은 경우에 오른쪽 꼬리가 길다.
p가 1/2보다 크면 왼쪽 꼬리가 길다.

확률 = $_nC_x \ p^x(1-p)^{n-x}$
기대값 = $E(x) = np$
분산 = $V(X) = np(1-p) = npq \ (\because q = 1-p)$

포아송 분포

단위 시간 또는 공간에서 발생하는 사건의 수를 나타낸 이산 확률 분포. 공정 진행 중 웨이퍼에서 defect이 발생할 가능성을 나타낼 수 있음.

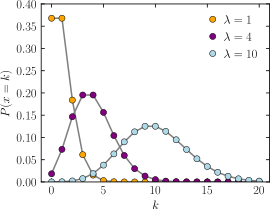
모수( $\lambda$ ) = 임의로 발생하는 사건의 평균 횟수
확률 = $\frac{e^{-\lambda}\lambda^x}{x!}$
평균 = $\lambda$
분산 = $\lambda$

$\lambda$ 이 매우 크고 $p$ 가 매우 작으면 $\lambda = np$ 로 근사 가능 (정규분포 따라감)

확률 밀도 함수

연속 확률 변수에서 분포를 나타냄.

지수 분포

첫번째 사건이 일어날 때 걸리는 시간에 대한 연속 확률 분포. 장비의 에러 예측하는데 쓰임.

확률 = $\lambda e^{-\lambda x}$
평균 = $\frac{1}{\lambda}$
분산 = $\frac{1}{\lambda ^2}$

어떤 시점부터 소요되는 시간은 과거 시간에 영향을 받지 않을 때 쓸 수 있음. (무기억성)

정규 분포

가우시안 분포라고도 불림. 평균이 0이고 표준편차가 1인 정규 분포를 표준정규분포(=z분포)라고 함. 좌우 대칭이며 첨도와 왜도가 0이다.

평균: $\mu$
분산: $\sigma^2$

첨도: 얼마나 뾰족한지를 나타냄. 이게 클 수록 데이터가 평균에 몰려있다.
왜도: 데이터가 얼마나 좌우대칭이 아닌지. 음수면 오른쪽으로 쏠려있다. (왼쪽으로 꼬리가 길다) 양수면 반대.

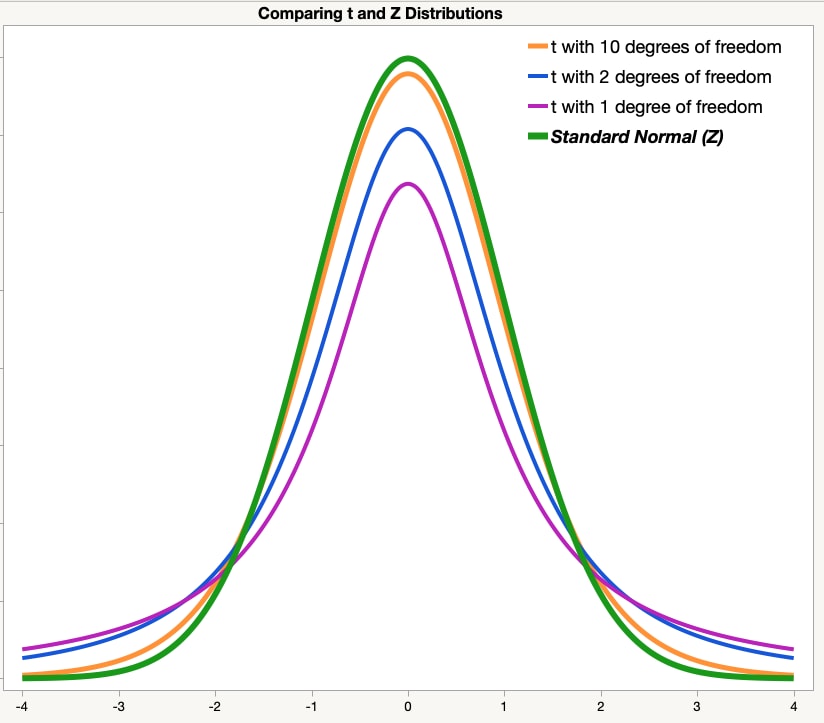
t분포

모집단의 평균값을 추론할 때 쓰는 분포. 정규분포랑 생긴 게 비슷하다. 좌우대칭인 건 같은데 t분포가 좀 더 낮다. 표본이 적을 때 사용한다.

확률변수 $t = (\bar X - \mu)\frac{\sqrt n}{S} = \frac{(\bar X - \mu)}{\frac{S}{\sqrt n}}$

$\frac{S}{\sqrt n}$ 는 표준오차

위의 그래프는 확률을 나타낸다. 따라서 그래프와 x축 사이의 공간의 넓이는 1이다.
t, z 분포에서 x축을 맡고 있는 t, z값은 평균에서 많이 떨어져있는 정도이다.

t값이 0일 때 가장 높은데, 그때의 y축이란 t가 0일 때의 확률, 즉 표본의 데이터들이 표본 평균과 가까울 확률을 말한다.
중요한 것은, 이 그래프에서 모집단의 평균 추정치를 알아낼 수는 없다는 것이다. 모평균의 추정치나 모평균이 있으리라 추측되는 구간은 따로 구하고, 그 구간을 t나 z값으로 바꿨을 때 그래프의 넓이(=확률)로 추정치가 그 구간 안에 있을 확률이 몇인지 따져보거나, 이쯤되면 유용하겠다 싶은 확률을 만드는 t, z값을 구한 뒤 그것과 표준편차를 이용해 추정 구간을 구할 수 있다.