entropy, cross-entropy를 공부하다가 KL-Divergence에 대해 좋은 글이 있어서 번역해보았다.
출처: https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained
Introduction
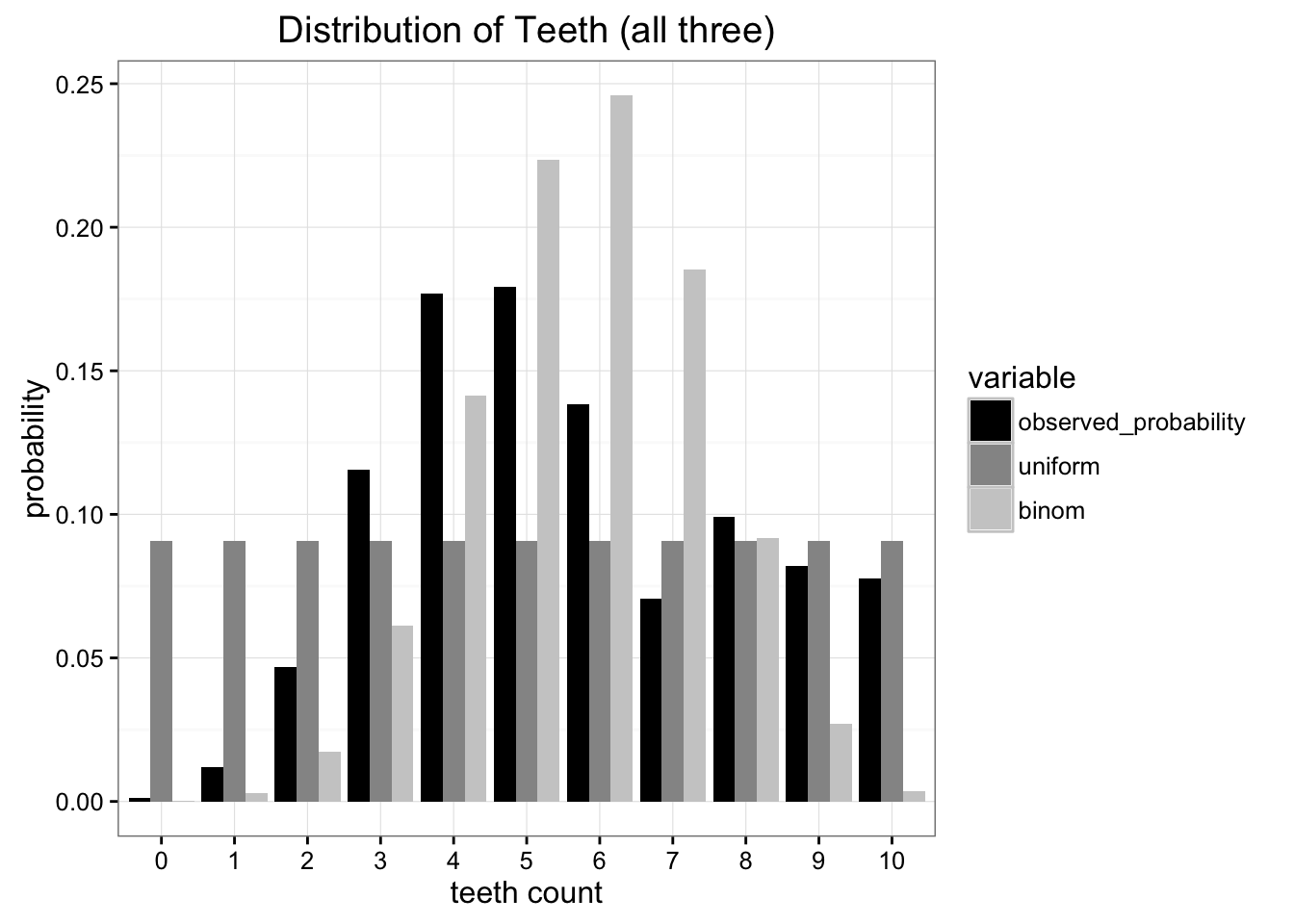
외계 행성에서 이상한 벌레를 발견했다.
이 벌레들의 이빨 개수의 분포를 우리는 경험을 통해 발견할 수 있었다.
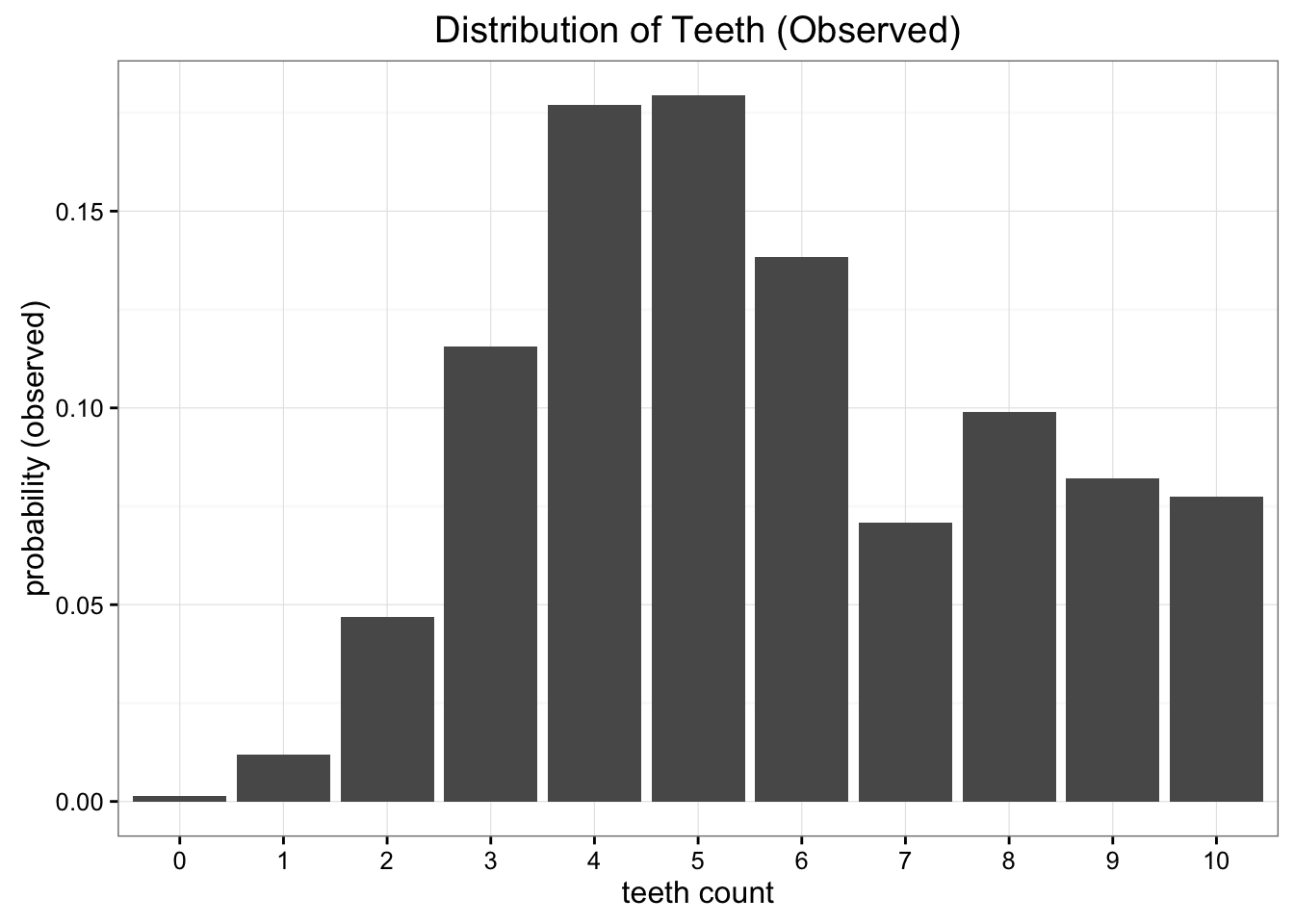
이제 이 놀라운 발견을 지구에 보내야한다. 우리는 자원이 부족하기 때문에, 가장 최소한의 비용으로 우리가 발견한 분포를 지구에 보내고자 한다 -> 이 분포를 나타내는 paramter의 개수를 최소로 하고 싶은 것이다. 그렇다면 어떤 분포를 사용해서 우리의 발견을 근사하도록 할 수 있을까?
uniform 분포?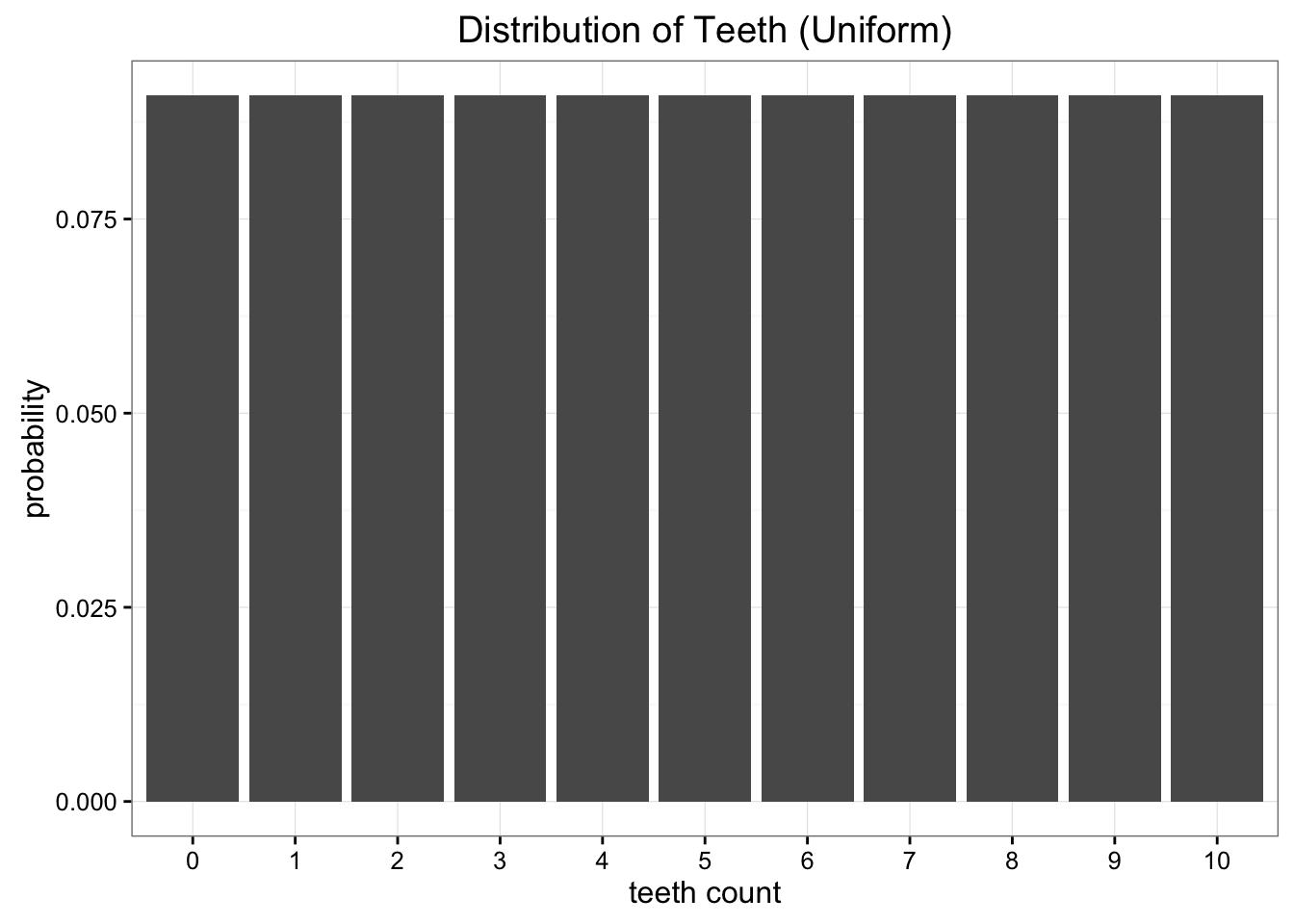
binomial 분포?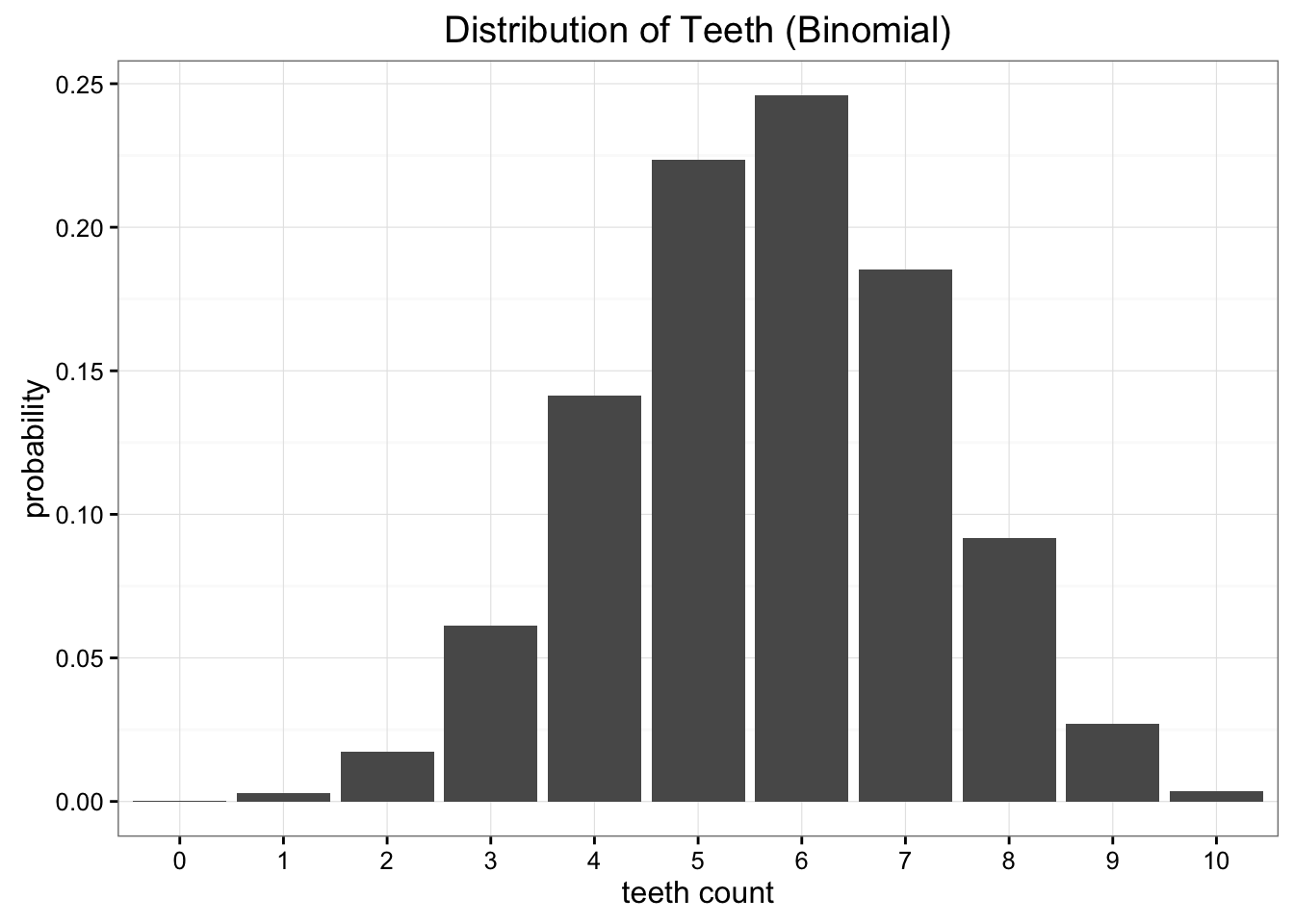
두 분포 모두, 우리가 발견한 원래 분포와는 차이를 보인다. 그렇다면, 둘 중 어떤 분포가 "좀 더 나은" 분포일까? 우리가 발견한 분포와 더 "가까운" 분포는 어떤 것일까?
여러가지 error metric이 있겠다만은, 우리의 원래 목적을 다시 떠올려보자.
우리는 지구에 보내는 정보의 양을 최소로 하고 싶은 것이다. 즉, parameter의 개수를 줄이고 싶은 것이다. 위의 두 모델(uniform, binomial)은 우리가 발견한 분포를 2개의 parameter로 압축해서 표현할 수 있게 한다.
둘 중, 더 나은 분포는, 두 분포 중 우리의 발견을 더 잘 나타내는, 즉, 더 많은 원본 정보를 담고있는 분포일 것이다.
여기서 KL- Divergence 개념이 들어온다.
The entropy of our distribution
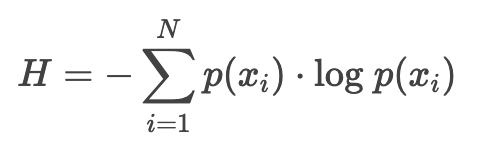
entropy는 the minimum number of bits it would take us to encode our information 이라고 할 수 있다. (log2로 나타내는 이유는 bit이 2진수이기 때문일 것이고)
이 entropy식이 우리에게 알려주지 않는 것이 있다. 이 정보를 압축하기 위해 필요한 encoding scheme을 알려주지 않는다 -> 이건 더 딥하게 따로 공부해야하지만 여기서는 넘기자.
entropy는 결국, 우리의 발견안에 얼마 만큼의 정보가 들어있는지를 qunatify할 수 있는 방법이라는 것이다. 이렇게 quantify할 수 있기 때문에, oberseved distribution-> parameterized distribution로 대체할 때 얼만큼의 정보가 손실되는 지도 quanitify할 수 있다는 것이다.
여기서의 oberseved distribution은 외계행성에서 발견한 벌레의 이빨 개수 분포이고, parameterized distribution은 지구로 보낼 때, 이 발견된 분포를 근사할 수 있느 분포를 의미한다.
Measuring information lost using Kullback-Leibler Divergence
our probability distribution : p
approximating distribution : q
이 두 분포의 차이는 다음과 같이 나타낼 수 있다.
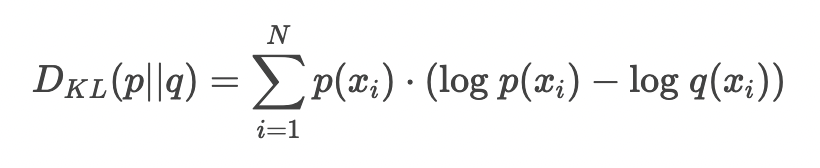
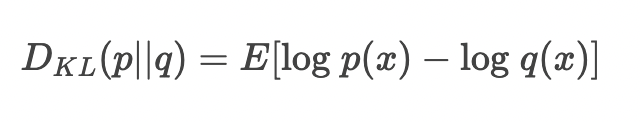
이 값은 p 를 q로 대체했을 때, 얼만큼의 정보 손실이 일어나는 가를 의미한다 (how many bits of information we expect to lose)
자, 그러면 다시 외계행성의 벌레 이빨 개수 문제로 돌아가자.


KLD를 계산해보면, binomial 분포로 근사했을 때의 정보손실량이 uniform 분포로 근사했을 때의 정보손실량보다 크다는 것을 알 수 있다. 그냥 uniform 분포를 써야될 것이다.
Optimizing using KL Divergence
Binomial 분포를 위해 하나의 값을 선택할 때, 우리는 확률의 parameter를 우리 데이터에 맞는 기댓값을 사용해서 결정한다.
그러나, 우리는 정보 손실을 최소화하기 위해 optimizing을 하는 것이므로, 이 방법이 parameter를 고르는데 best가 아니라는 것을 알고 있다.
parameter값이 변함에 따라 KLD가 어떻게 변하는지를 살펴보자.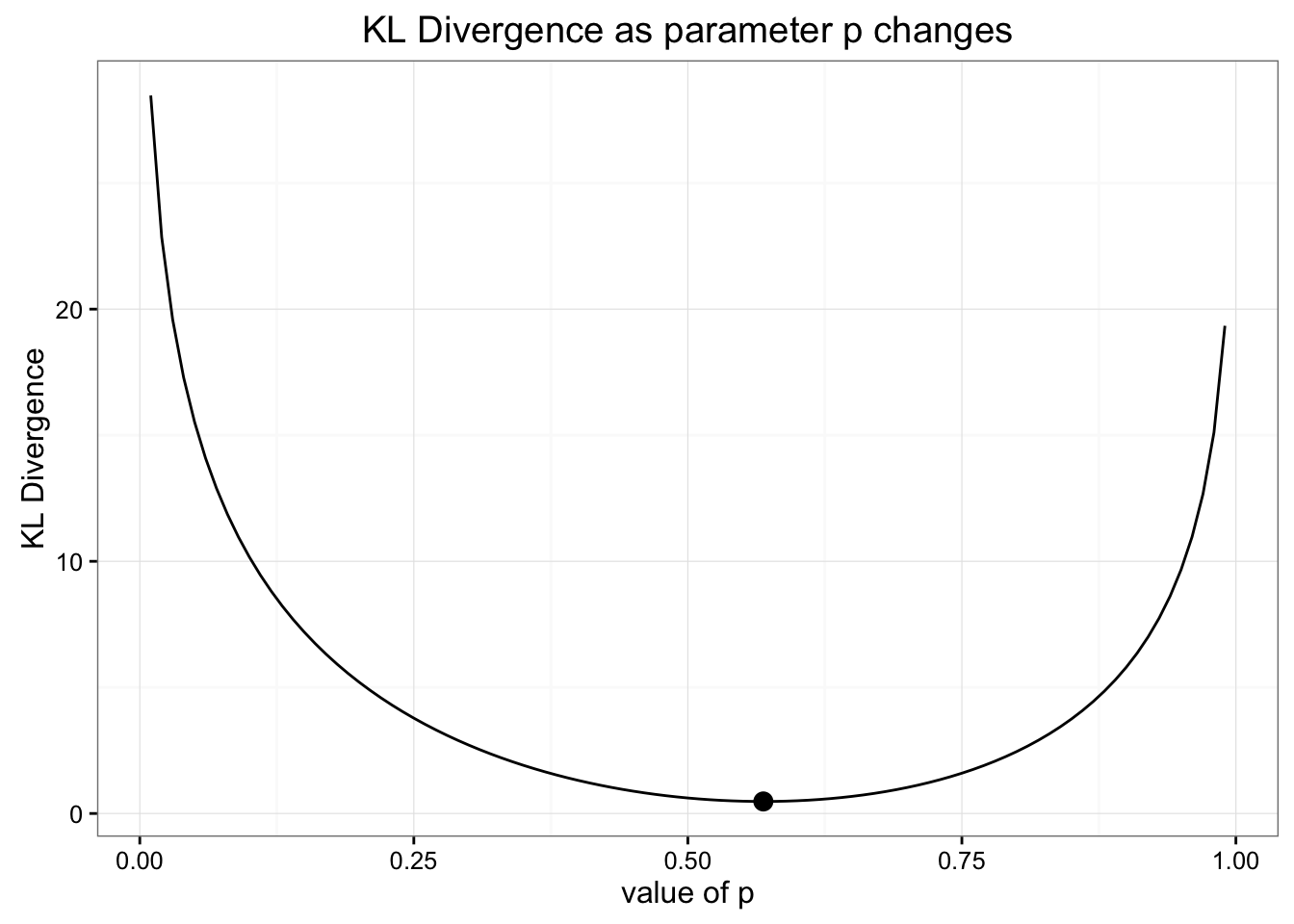
우리의 binomial 분포의 예측값이 KLD를 최소화 할 수 있는 best estimate였다는 것을 다시 확인할 수 있다.
우리의 발견 데이터를 모델링하기 위해 ad hoc distribution 을 만든다고 가정해보자.
데이터를 두 개로 쪼개보면, P(이빨 개수 = 0~5)과 P(이빨 개수 = 6~10)으로 나눌 수 있다. 그런 다음 하나의 parameter로 total probability dist가 이 분포의 오른쪽(이빨 개수 = 6~10)에 떨어질 percentage를 구해보자 (-> likelihood)
예를 들어, parameter =1로 설정하면, (이빨 개수 = 6~10)은 각각 0.2의 확률을 가질 것이고, (이빨 개수 = 0~5)그룹의 모든 확률은 0이 될 것이다.
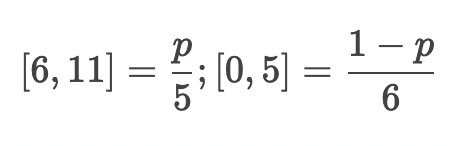
(이빨 개수 = 6~10) 그룹에 할당된 확률 p에 (6,7,8,9,10)-> 5가지 경우가 p를 나눠가짐
(이빨 개수 = 0~5) 그룹에 할당된 확률 1-p에 (0,1,2,3,4,5)-> 6가지 경우가 1-p를 나눠가짐
이런 이상한 모델에 대해서 최적의 parameter를 어떻게 찾을 수 있을까? 이전에 했던 것처럼 KLD를 최소화해보자
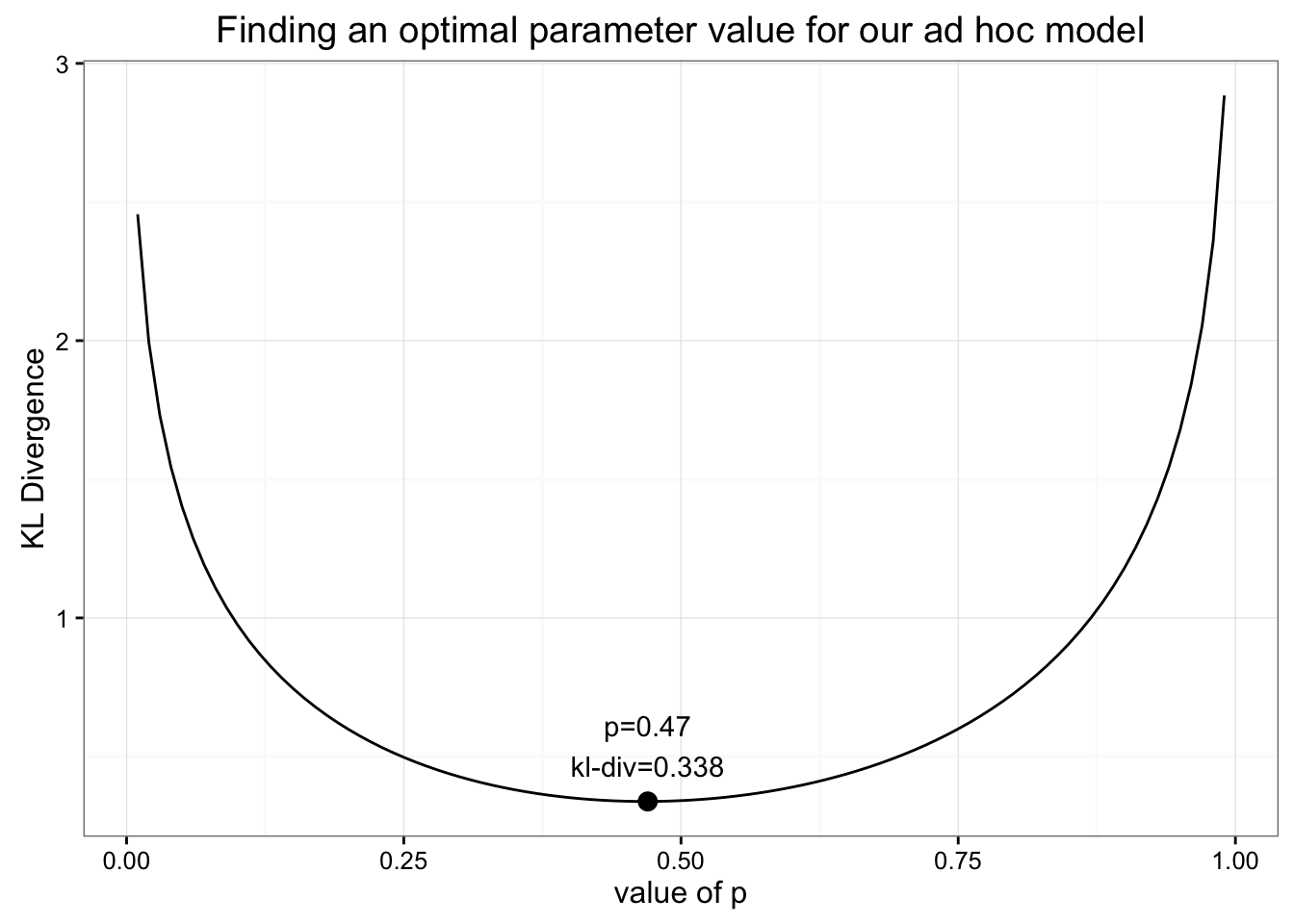
min value of KLD = 0.338 when p=0.47
-> uniform 분포에서 얻었던 값과 동일하다! (revisited)
(revisited)
우리의 ad hoc모델의 분포를 그려보면 다음과 같다
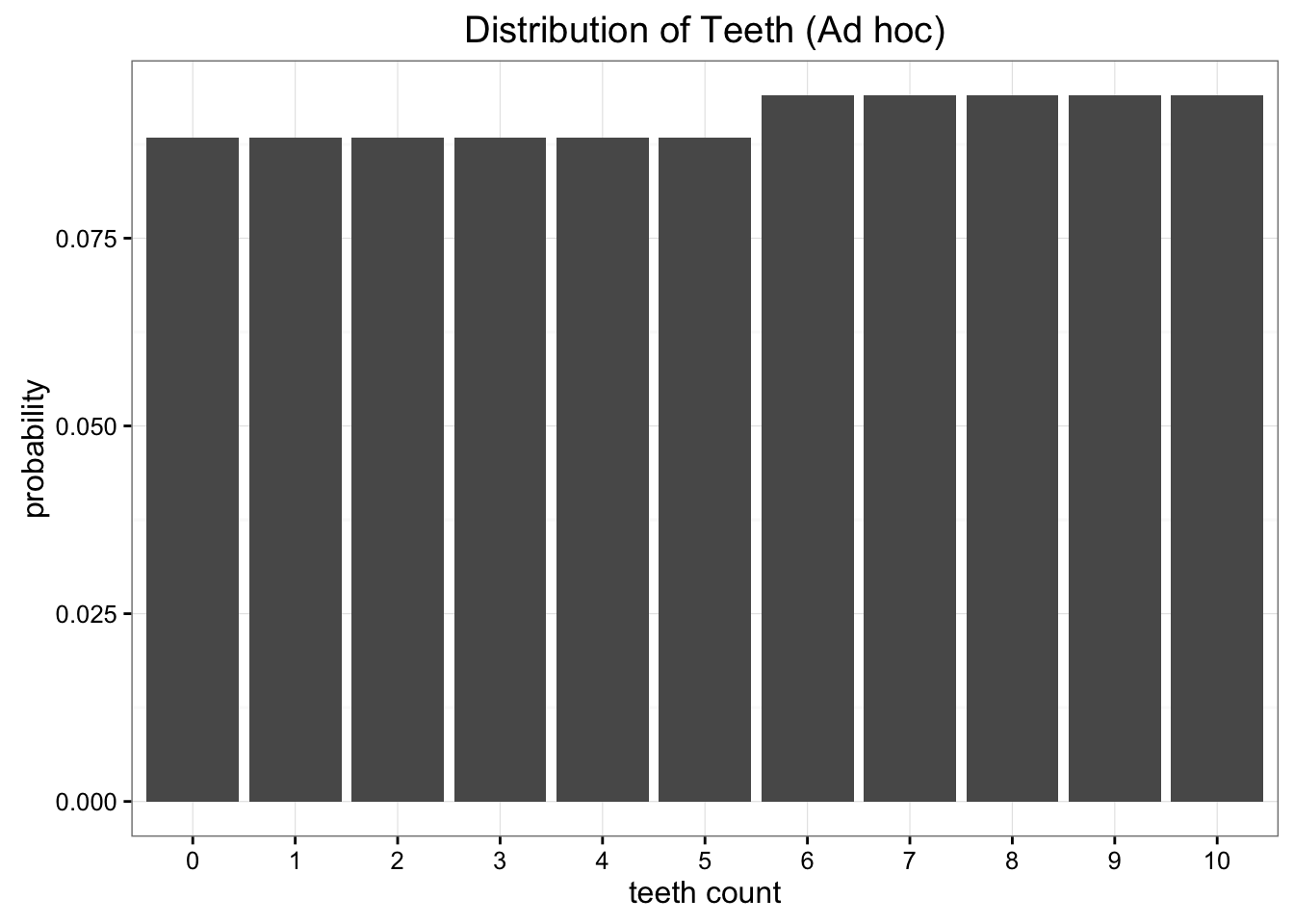
ad hoc모델을 써도 정보 손실을 줄일 수 없으니, 그냥 uniform모델을 쓰는게 낫다는 결론이 나온다.
결론적으로, KLD의 key point는 어떤 분포를 근사하는 분포의 optimal parameter를 찾기 위한 목적함수가 된다는 것이다
