Dataset shift

Dataset shift는 학습데이터와 테스트 데이터에서의 인풋과 아웃풋의 joint distribution가 다른 경우를 의미한다. 다시 말해, 학습데이터셋과 테스트셋의 분포가 다른 경우라고 생각하면 된다.
Data shift 문제는 supervised, semi-supervised ML에서 주로 발생한다(data shift의 전제가 학습 셋과 테스트 셋이 있다는 것이니, supervised/semi-supervised ML에서 발생하는 것이 당연하다)
data shift의 다양한 manifestation
- Covariate shift
- Prior probability shift
- Concept shift
- Internal covariate shift (an important subtype of covariate shift)
Covariate shift
독립변수들 간의 공변량(covariate)의 분포가 변화하는 현상을 말한다. 표본의 대표성 문제와 관련되어있다고 생각해도 좋을 것 같다. 전체 데이터셋의 분포를 잘 반영하는 학습/테스트 셋이 아니기 때문에, 표본의 대표성이 떨어진다고 볼 수 있다고 생각한다.
이는 보통 latent 변수들 때문에 발생한다.

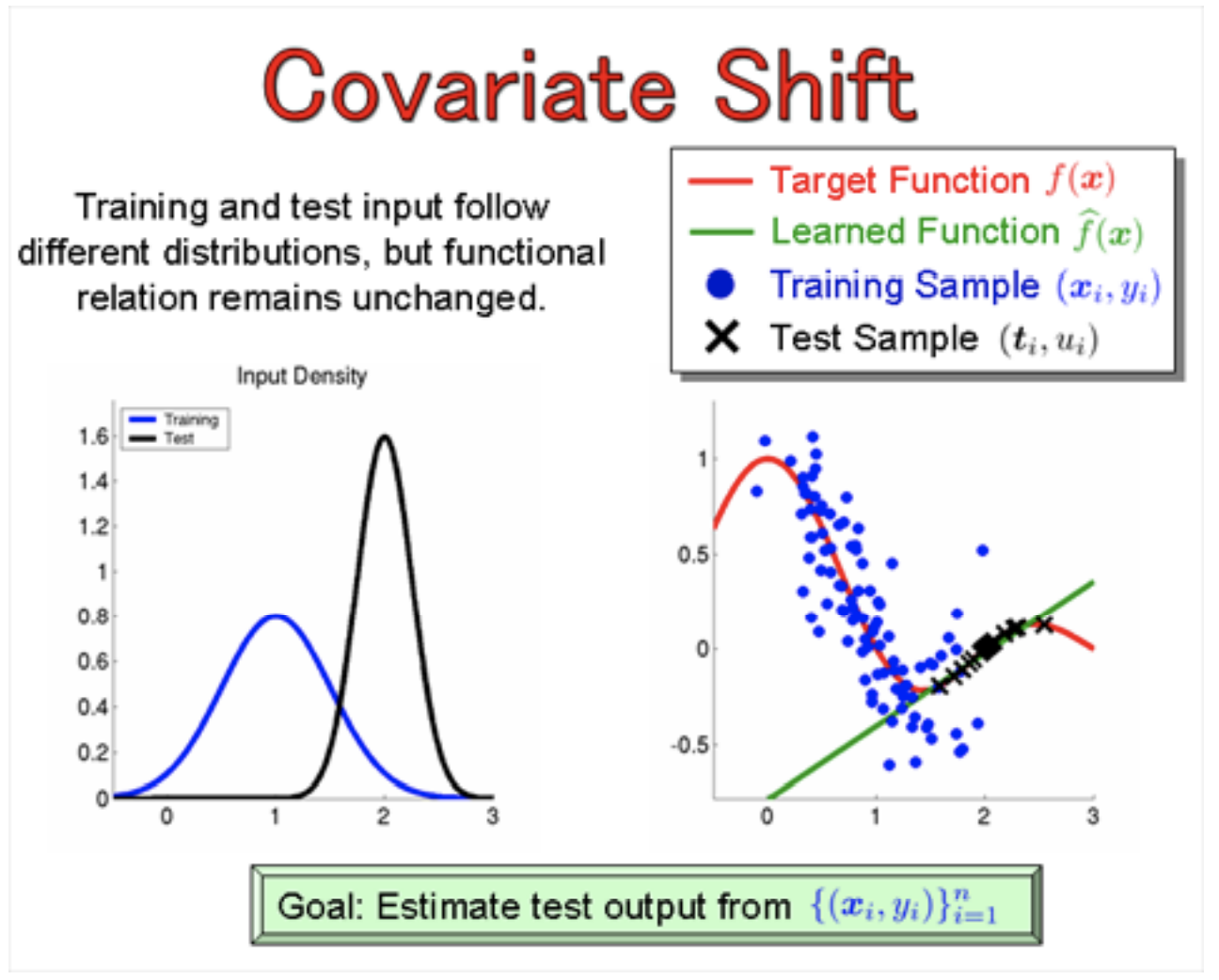
들어가는 것(input; x)은 달라도 나오는 것(output; y)은 똑같다.
예를 들어, 얼굴 인식 모델에서, 학습데이터는 어린 아이들이 대부분이 데이터로 하고, 테스트셋은 노인들이 대부분인 데이터로 하는 경우가 있다.
이렇듯 학습셋과 테스트셋이 동일 분포를 반영하고 있지 않다면, input과 Output 간의 내재된 관계성은 변하지 않지만, 그 관계성은 부분적으로는 data-sparse, omitted, misrepresented되어 있다. 이 예시에서는 어린아이들의 데이터로 학습되었으니, 청년~노인층까지의 데이터가 희소하고, 빠져있기 때문에, 대표성이 부족하다고 할 수 있다.
특히, covariate shift 문제가 있는 데이터에서 cross-validation을 할 때, 심하게 왜곡될 수 있다. cross validation은 전체 데이터는 n fold만큼 잘라서 (n-1) fold는 학습셋으로, 나머지 1fold는 테스트 셋으로 나눈 validation을 의미한다. 이렇게 전체데이터의 분포가 극단으로 치우쳐져있다면, 잘못해서 학습셋에는 어린아이들의 사진만! 테스트셋에는 노인들의 사진만! 들어가있을 수 있기 때문에, 심하게 bias될 수 있다.

Prior Probability Shift
covariate shift가 x변수의 분포에만 집중한다면, prior probability shift는 종속변수 y의 분포에 집중한다. Covariate shift의 반대라고 생각하면 된다. 가장 직관적인 예시로는, unbalanced dataset을 생각하면 된다. 예를 들어, 코로나 확진 여부를 0(음성)과 1(양성)으로 나타냈을 때, 0이 압도적으로 많은 unbalanced data가 있을 것이다.
사전 확률을 잘 기억하자

오직 Y -> X일 때 발생하는 문제이며, 보통 나이브 베이즈 문제와 관련되어있다.
스팸메일을 받을 사전확률이 0.5일때, 우리는 아마도 메일 중 50%는 스팸, 50%는 일반메일일 것이라고 기대할 것이다. 그러나, 실제로 우리가 받는 90%의 메일이 스팸인 경우, Y에 대한 우리의 사전확률은 달라진다. data sparsity와 biased feature selection이 output distribution에 영향을 준다.

이 그림에서, 학습셋과 테스트셋에서 y값의 분포는 상이하나, x1과 x2의 분포는 비슷하게 구성된 것을 볼 수 있다.
Concept Drift
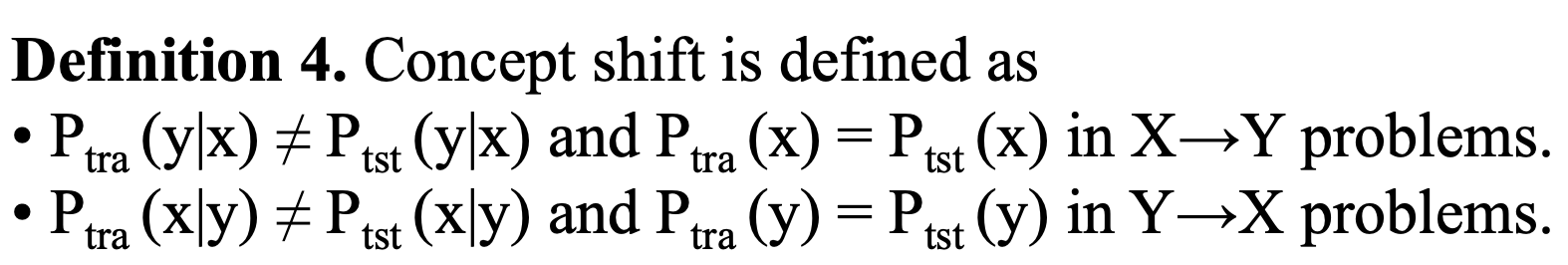
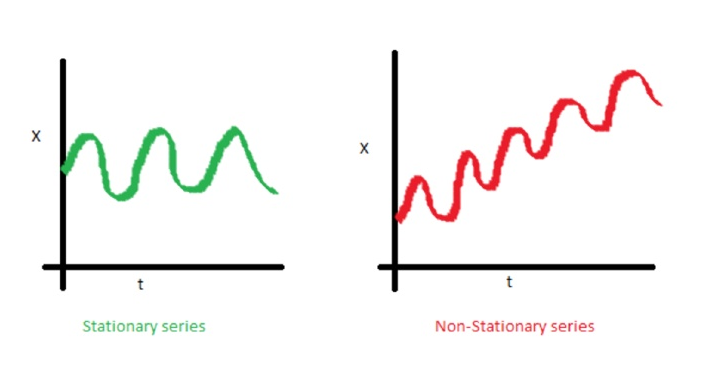
이 문제는 데이터(x,y) 분포에 관련된 것이 아니라, 두 변수간의 관계성에 대한 것이다. 직관적으로는, 시계열데이터 분석을 생각해보자.
시계열 분석에서, stationary(고정된) 시리즈를 분석하는 것이 non-stationary 시리즈를 분석하는 것보다 보편적이다. 왜 그럴까?
전자에서는 input과 output간의 관계가 지속적으로 변화하지 않기 때문에 분석하기 더 쉽기 때문이다.
예를 들어, 2008 금융위기 전의 기업이익을 분석하고, 여러 요인을 기반으로 기업이익을 예측하려고 한다. 만일 우리의 알고리즘이 2002-2007의 데이터를 학습했다면, 2008 금융위기 이후에는 잘 작동하지 않을 것이다. 뭐가 달라진걸까?
금융위기라는 사회변화 때문에 input과 output간의 관계가 달라졌고, 만약 이러한 관계의 변화가 우리의 변수들에 적용이 되지 않았으면(금융위기 전/후를 dummy 변수로 처리한다던지 하는..) 우리의 모델은 concept shift에 골머리를 썩고 있을것이다.
Internal Covariate Shift
Internal Covariate Shift가 최근 관심을 많이 받게 된 이유는, Neural Net의 hidden layer에서 covariance shift의 영향을 의심할 수 있었기 때문이다.
연구자들은 주어진 hidden layer의 output으로 부터 온 activation의 분포가 변동하는 것을 찾아냈다. 이때 activation은 그 다음 연속된 layer의 인풋이 되기 때문에, NN은 Covariate Shift에 방해를 받을 수 있다는 것이다. 이로 인해, batch normalization이 대두되었다.
batch norm layer는 (서로 다른 배치 사이의 평균 및 표준 편차에 내재된 노이즈 때문에) mini batch의 mean, std를 받고 이를 이용해서 인풋을 standardize한다. 또한 약간의 noise를 인풋에 더해줘서 네트워크를 regularize하는 역할도 수행한다.
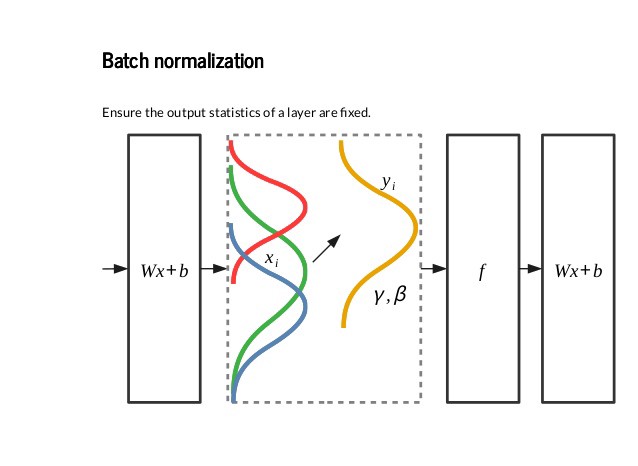
https://data-newbie.tistory.com/354
https://towardsdatascience.com/understanding-dataset-shift-f2a5a262a766
Importance-Weighted Cross- Validation for Covariate Shift (Masashi Sugiyama , Benjamin Blankertz)
