회귀분석은 전통적으로 통계학에서 많이 사용된 분석 방법이다. 여러 데이터를 기반으로 변수 간의 관계에 대한 적합도를 측정하는 분석법이다.
들 수 있는 예시는 아래와 같다.
- 공부 시간과 성적 사이의 관계
- 컴퓨터 스펙을 이용한 가격 예측
- 1인당 국민 총소득과 전기 사용량 사이의 관계
각 예제들의 공통점은 독립변수(independent variable)와 종속변수(dependent variable) 사이의 관련성을 밝히는 것이다.
이런 회귀의 개념은 영국의 우생학자 F. Galton(1822~1911)이 처음 제시했고, 아래는 아버지의 키와 자식의 키 사이의 관계에 대한 데이터와, 이를 토대로 그려본 직선 형태의 함수 관계도이다.
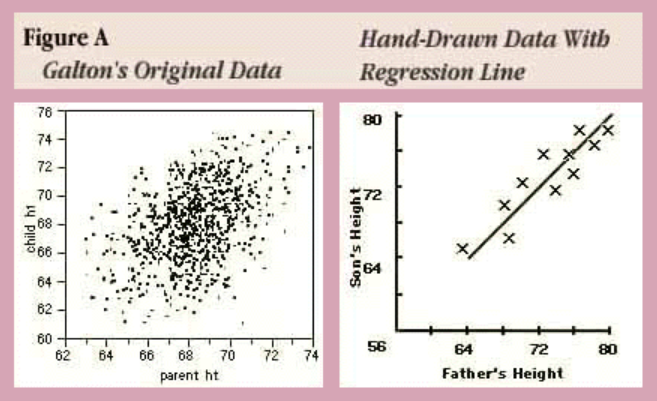
[출처 : http://www.biostat.jhsph.edu/courses/bio653/misc/JMPer%20Cable%20Summer%2098%20Why%20is%20it%20called%20Regression.htm]
위 그림과 같이 직선형태를 갖고 분석하는 것을 선형 회귀분석(Linear Regression)이라고 한다.
지도학습의 종류
- 분류 : 데이터 x의 여러 feature 값들을 이용하여 해당 데이터의 클래스 y를 추론하는 것
- 회귀 : 데이터 x의 여러 feature 값들을 이용하여 연관된 다른 데이터 y의 정확한 값을 추론하는 것
선형 회귀(Linear Regression)
가장 대표적인 회귀 분석 방법이다. 종속변수 y와 한 개 이상의 독립변수 x간의 선형의 상관관계를 만드는 회귀분석 방법이다. 독립변수의 개수에 따라 단순이냐, 다중이냐로 나뉜다.
경사하강법(Gradient Descent)
회귀 모델에서 적절한 회귀계수를 찾기 위해서는 손실함수의 설정이 중요하다. 따라서 가중치의 미분값이 최소가 되는 지점이 손실함수를 최소로 하는 지점이라고 가정한다.
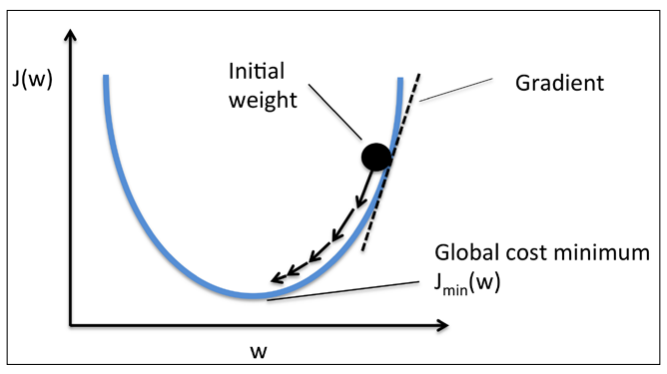
[출처 : https://lsh424.tistory.com/9]
이 손실함수를 최소로 하려면 기울기 값이 가장 작은 곳에 놔야하는데 우리는 최소 지점까지 가기위해 기울기 값을 learning rate를 이용해 업데이트한다. learning rate값이 크면 빨리 수렴이 가능하지만, 최적값을 건너뛰게 될 수 있다는 문제가 있다. 즉, 적절한 learning rate을 선정하는 것이 중요하다.
로지스틱 회귀(Logistic Regression)
로지스틱 회귀분석은 데이터가 어떤 범주에 속할지를 0과 1사이의 값으로 예측하고 분류하는 방법이다. 보통 이진분류 문제를 로지스틱 회귀분석으로 푼다. 예를 들면, 암에 걸렸다, 안걸렸다와 같은 문제를 풀기에 적합하다.
이렇게 보면 로지스틱 회귀는 회귀가 아닌 분류 문제로 볼 수 있다. 하지만, 모델이 반환하는 값이 연속적인 변수라서 회귀모델에 부합한다.
