비지도학습(Unsupervised learning)은 정답(Label)이 있는 데이터를 가지고 학습하는 지도학습(Supervised learning)과 달리 정답이 없는 데이터로 학습하는 방법이다.
즉, 모델 스스로가 데이터의 특징 및 패턴을 판단하는 것을 의미한다.
지도학습의 대표적인 예로는 분류가 있다. 강아지와 고양이 사진을 두고 각 사진이 어떤 동물인지를 판단하는 것이다. 이때 사진마다 '강아지', '고양이'라는 정답(Label)이 필요하다. 하지만 이렇게 레이블링된 데이터셋을 만들기 위해서는 많은 인적자원이 소모된다.
이런 문제를 해결하고자 나온것이 비지도 학습이다. 비지도 학습의 대표적인 예로는 군집화(Clustering)가 있다. 군집화 외에도 차원 축소(dimensionality reduction), 생성모델 이용 등 다양한 예가 있다.
군집화
군집화란 정답(Label)과 같이 명확한 분류 기준이 있는 것이 아닌 정답이 없는 데이터들을 분석하여 유사한 특징을 갖고 있는 데이터들끼리 묶는 작업이다.
1) K-means
K-means 알고리즘은 k값이 주어질 때, 데이터를 k개의 군집으로 묶는 군집화 알고리즘이다. 하지만 이런 알고리즘도 아래와 같은 상황에서는 적합하지 않다.
- 군집의 개수가 지정되어 있어야 하기 때문에 이를 모를 경우에는 사용이 어렵다.
- 유클리드 거리가 가까운 데이터끼리 군집이 형성되므로 연관된 데이터의 분포가 멀면 사용이 어렵다.
유클리드 거리
2) DBSCAN
DBSCAN(Density Based Spatial Clustering of Applications with Noise) 알고리즘은 밀도 기반의 군집화 알고리즘이다. K-means 알고리즘 사용이 어려운 경우에 사용하면 된다.
DBSCAN은 K-means와 같이 군집의 개수가 필요하지 않다. 또 밀도 기반이기 때문에 원모양이나 불특정한 모양의 군집도 탐색이 가능하다.
즉, 보다 유연한 사용이 가능하다. 하지만 이런 알고리즘도 단점이 있다. 바로 데이터의 수가 많아지면 알고리즘 수행시간이 급격하게 늘어난다는 점이다.
import time
n_samples= [100, 500, 1000, 2000, 5000, 7500, 10000, 20000, 30000, 40000, 50000]
k_time = []
db_time = []
x = []
for n_sample in n_samples:
# 원형의 분포 데이터 생성
dummy_circle, dummy_labels = make_circles(n_samples=n_sample, factor=0.5, noise=0.01)
# K-means 시간 측정
k_start = time.time()
circle_k = KMeans(n_clusters=2)
circle_k.fit(dummy_circle)
k_end = time.time()
# DBSCAN 시간 측정
db_start = time.time()
epsilon, minPts = 0.2, 3
circle_db = DBSCAN(eps=epsilon, min_samples=minPts)
circle_db.fit(dummy_circle)
db_end = time.time()
x.append(n_sample)
k_time.append(k_end - k_start)
db_time.append(db_end-db_start)
print("# of samples: {} / Elapsed time of K-means: {:.5f}s / DBSCAN: {:.5f}s".format(n_sample, k_end - k_start, db_end - db_start))
# 소요 시간 그래프 그리기
fig = plt.figure()
ax = fig.add_subplot(1, 1, 1)
ax.scatter(x, kmeans_time, c='blue', marker='D', label='K-means elapsed time')
ax.scatter(x, dbscan_time, c='purple', marker='x', label='DBSCAN elapsed time')
ax.set_xlabel('# of samples')
ax.set_ylabel('time(s)')
ax.legend()
ax.grid()
/------------------------------------------------------------------------------------------------------------------------------------/
# 출력
# of samples: 100 / Elapsed time of K-means: 0.02081s / DBSCAN: 0.00113s
# of samples: 500 / Elapsed time of K-means: 0.01525s / DBSCAN: 0.00227s
# of samples: 1000 / Elapsed time of K-means: 0.01614s / DBSCAN: 0.00608s
# of samples: 2000 / Elapsed time of K-means: 0.01245s / DBSCAN: 0.01146s
# of samples: 5000 / Elapsed time of K-means: 1.03900s / DBSCAN: 0.04419s
# of samples: 7500 / Elapsed time of K-means: 1.00253s / DBSCAN: 0.10479s
# of samples: 10000 / Elapsed time of K-means: 1.12395s / DBSCAN: 0.12250s
# of samples: 20000 / Elapsed time of K-means: 0.94238s / DBSCAN: 0.34835s
# of samples: 30000 / Elapsed time of K-means: 1.23537s / DBSCAN: 0.61363s
# of samples: 40000 / Elapsed time of K-means: 1.21754s / DBSCAN: 1.17958s
# of samples: 50000 / Elapsed time of K-means: 1.13880s / DBSCAN: 1.96405s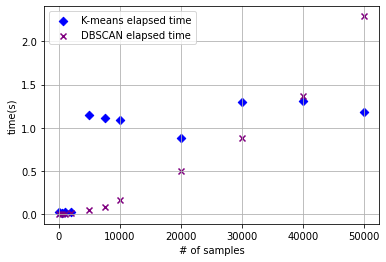
참고자료
차원 축소
PCA
비지도 학습의 방법 중 하나인 차원 축소에는 PCA(주성분분석)이라는 알고리즘이 있다. 차원 축소는 데이터의 여러 특징 중 가장 그 데이터를 잘 표현하는 특징을 추출하는 특징 추출(feature extraction)의 용도로 사용된다. PCA는 주성분 분석이라고 한다. 여기서 주성분은 데이터의 분산이 가장 큰 방향 벡터를 의미한다. PCA는 데이터의 분산을 최대로 보존하고, 서로 직교(orthogonal)하는 기저(basis, 분산이 큰 방향벡터의 축)들을 찾아 고차원 공간을 저차원 공간으로 사영(projection)한다.
