모든 정점간 최단 경로 문제

• 모든 정점간 최단 경로(All Pairs Shortest Paths) 문제
  • 모든 정점들 간의 최단 경로를 찾는 문제
• 다익스트라로 문제를 해결하기 위해서는 정점 수 만큼 반복해야 함: O(n^3)

---

1. 플로이드-와셜(Floyd-Warshall) 알고리즘

• 간단히 플로이드 알고리즘으로 부르기도 함
• 플로이드 알고리즘의 시간 복잡도는 O(n^3)으로 다익스트라 알고리즘을 n번 사용할 때의 시간복잡도와 동일
  • 하지만 플로이드 알고리즘이 훨씬 간단하기 때문에 구현및 활용하기에 용이

2. 수행과정

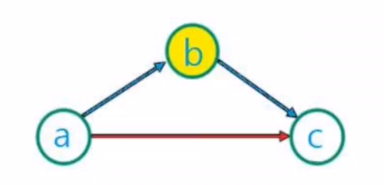
• a에서 c로 가는 경로 중 가장 짧은 것을 선택
  

2.1. 부분 문제 정의

(Dij)^k: 정점{1,2,...,k}를 경유 가능한 정점으로 고려하여, 정점 i에서 j까지의 모든 경로 중에서 가장 짧은 경로의 거리를 의미

1) (Dij)^1

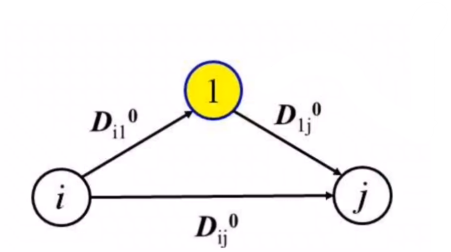
2) (Dij)^2

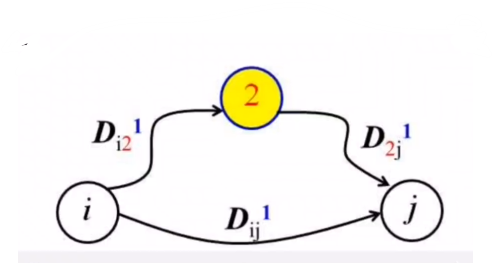
k) (Dij)^k

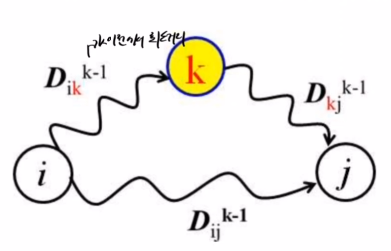
2.2. 알고리즘

3. 시간 복잡도

• 각 k에 대해 모든 i,j쌍에 대해 계산되니: O(n^3)