Algorithm
1.Algoritm 썸네일

업로드중..
2.[알고리즘1] 알고리즘의 기본 조건과 분석

문제를 해결하는 단걔적 절차 또는 방법정확성: 알고리즘은 주어진 입력에 대해 올바른 해를 도출해야 함수행성: 알고리즘의 각 단계는 컴퓨터에서 수행 가능해야 함유한성: 알고리즘은 유한 시간 내에 종료 되어야 함효율성: 알고리즘은 효율적일 수록 가치가 높아짐유클리드의 최대
3.[알고리즘1] 분할 정복 알고리즘
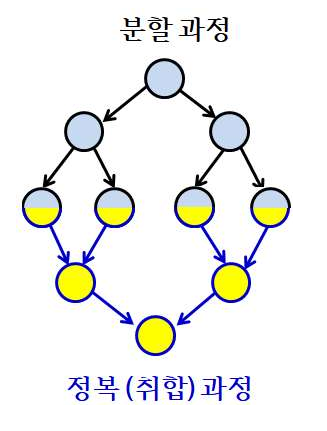
주어진 문제의 입력을 분할하여 문제를 해결하는 방식의 알고리즘분할한 입력에 대해 동일한 알고리즘을 적용하여 해를 계산부분 문제이들의 해를 취합하여 원래 문제의 해를 얻음부분 해부분 문제를 더 이상 분할할 수 없을 때까지 분할문제가 2개로 분할되고 부분 문제의 크기가 일
4.[알고리즘1] 분할정복_합병정렬

입력이 2개의 부분 문제로 분할되고, 부분 문제의 크기가 1/2로 감소하는 분할정복 알고리즘알고리즘 실행 과정n개의 데이터들은 n/2개씩 2개의 부분문제로 분할더 작은 부분 문제들로 불할할 수 없을 때 까지 주어진 데이터들을 계속해서 분할두 데이터를 합병정렬하여 정렬(
5.[알고리즘1] 분할정복_퀵 정렬

부분 문제의 크기가 일정하지 않은 형태의 분할 정복 알고리즘퀵 정렬은 피봇(pivot)이라 일컫는 배열의 원소를 기준으로 함피봇보다 작은 숫자들은 왼쪽, 큰 숫자는 오른쪽으로 분할분할 시, 피봇은 분할된 배열에 포함되지 않고 위치가 고정됨위의 과정을 순환전체 의사코드부
6.[알고리즘1] 분할정복_선택문제

n개의 숫자들 중에서 k번째로 작은 숫자를 찾는 문제k번째로 작은 숫자를 찾는 간단한 방법방법1: 최소 숫자를 k번 찾기 O(kn)방법2: 숫자들을 정렬한 후, k번째 숫자 찾기 O(nlogn)이 문제도 탐색 문제의 일종으로 이진탐색을 사용 가능정렬된 리스트에서 중간에
7.[알고리즘1] 분할정복_최근접 점의 쌍 찾기
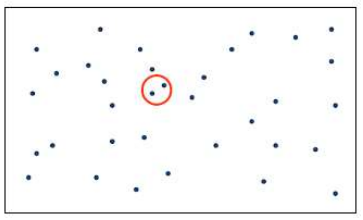
2차원 평면 상의 n개의 점이 입력으로 주어질 때,거리가 가장 가가운 한 쌍의 점을 찾는 문제모든 두 점의 거리를 계산시간복잡도nC2 = n(n-1)/2 = O(n^2)한쌍의 거리계산: O(1)O(1)\*O(n^2) = O(n^2)n개의 점을 1/2개로 분할하여 각 부
8.[알고리즘1] 그리디 알고리즘
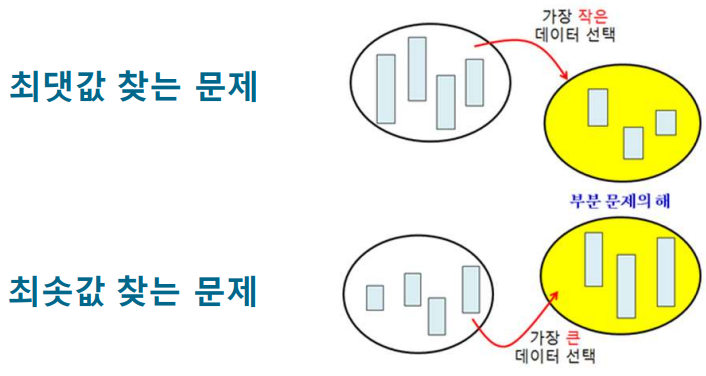
최적화 문제를 해결하는 알고리즘최적화(optimization) 문제: 가능한 해들 중에서 가장 좋은 해를 찾는 법욕심쟁이 방법, 탐욕적 방법, 탐욕 알고리즘 등으로 불림그리디 알고리즘은 데이터 간의 관계를 고려하지 않고 수행 과정에서 '욕심내어' 최소값 또는 최대 값을
9.[알고리즘1] 그리디_거스름돈,배낭 문제

최소의 동전 개수로 거스름돈을 거슬러주는 문제남은 액수를 초과하지 않는 조건에서 '욕심내어' 가장 큰 금액을 갖는 동전을 취하는 것그리디 알고리즘의 근시안적인 특성CoinChange 알고리즘은 남아있는 거스름돈인 change에 대해 가장 높은 가격을 갖는 거스름돈을 제
10.[알고리즘1] 그리디_MST_Kruskal
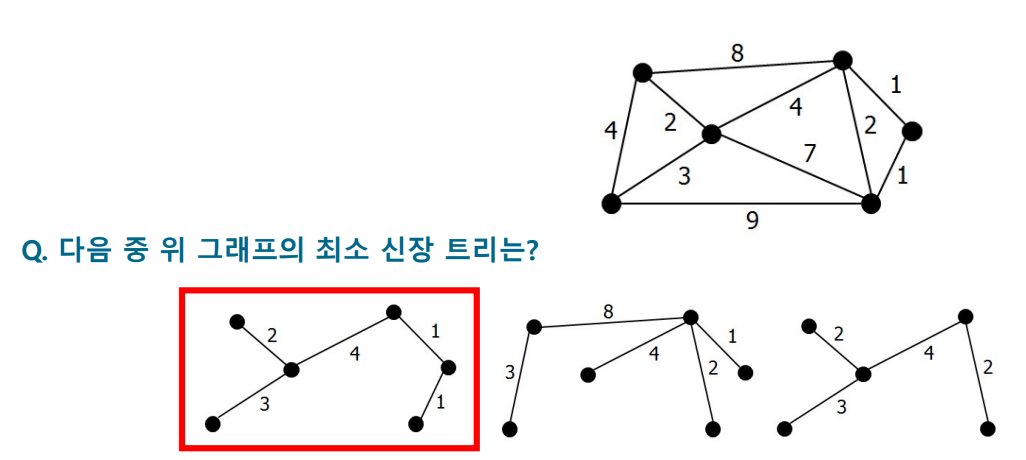
주어진 가중치 그래프에서 사이클이 없이 모든 점들을 연결시킨 트리 중에서 간선들의 가중치 합이 최소인 트리주어진 그래프의 신장 트리를 찾는 법사이클이 발생하지 않도록 모든 정점을 연결그래프 내의 정점의 수 = n신장 트리에는 정확히 (n-1)개의 간선이 존재트리에는 간
11.[알고리즘1] 그리디_MST_Prim
시작 정점에서 출발하여 신장 트리 집합을 단계적으로 확장해나가는 방법Kruskal 알고리즘과 달리 그래프의 정점을 추가하는 과정을 통해 최소 신장트리를 구축Prim 알고리즘의 MST 구축 순서시작 단계에서는 시작 정점만이 신장 트리 집합에 포함앞 단계에서 만들어진 신장
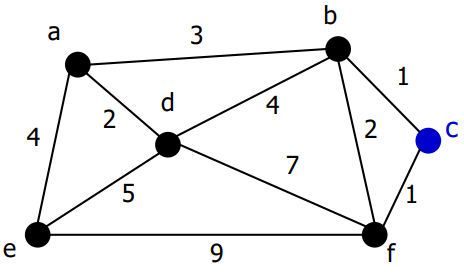
12.[알고리즘1] 그리디_다익스트라 알고리즘
최단 경로 문제주어진 가중치 그래프에서 어느 한 출발점에서 또 다른 도착점까지의 최단경로를 찾는 문제최단 경로를 구하는 알고리즘 종류단일 정점으로부터 나머지 모든 정점가지의 최단거리를 계산하는 알고리즘모든 정점간 최단 거리를 계산하는 알고리즘음의 가중치가 없는 그래프에
13.[알고리즘1] 집합 커버 문제
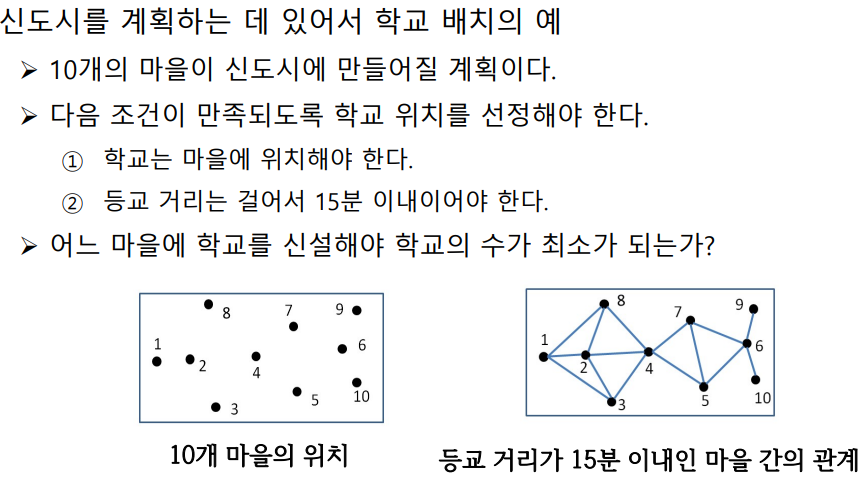
문제 설명n개의 원소를 가진 집합 UU의 부분집합들을 원소로 하는 집합 F가 주어짐F의 원소들로 구성된 집합 중에서 어떤 집합들을 선택하여 합집합 연산을 수행하면 집합 U와 같게 되는가?집합 F에서 선택하는 집합들의 수를 최소화하는 문제2번 마을에 학교를 만들면1,2,
14.[알고리즘1] 그리디_작업 스케줄링
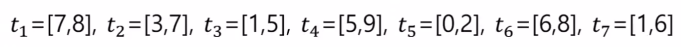
작업의 수행 시간이 중복되지 않도록 모든 작업을 가장 적은 수의 기계에 배정하는 문제작업의 수각 작업의 시작시간과 종료시간작업의 길이(종료시간-시작시간)빠른 시작 시간 작업 우선 배정법빠른 종료시간 작업 우선 배정법짧은 작업 우선 배정법긴 작업 우선 배정법위 방법 중
15.[알고리즘1] 그리디_허프만 코딩과 압축
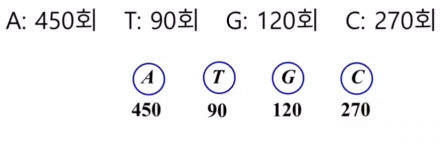
파일의 각 문자가 8bit인 아스키 코드로 저장되면, 그 파일의 bit수는 8x(파일의 문자 수)가 됨이 때, 파일의 각 문자는 일반적으로 고정된 크기의 코드로 표현고정된 크기의 코드로 구성된 파일을 저장하거나 전송할 때 파일의 크기를 줄이고, 필요시 원래의 파일로 변
16.[알고리즘1] 동적계획 알고리즘
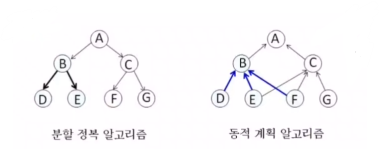
입력 크기가 작은 부분 문제들을 우선적으로 해결이전에 해결한 해를 이용해 큰 크기의 부분 문제들을 해결최종적으로 원래 주어진 입력의 문제를 해결가능동적 계획 알고리즘은 문제가 분할되는 구간이 없음동적 계획 알고리즘은 부분 문제들 사이에 의존적 관계가 존재함이러한 관계가
17.[알고리즘1] 동적계획_플로이드-와셜
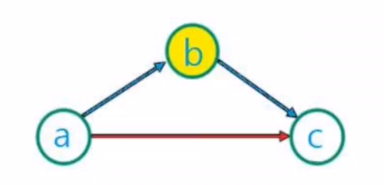
모든 정점간 최단 경로(All Pairs Shortest Paths) 문제모든 정점들 간의 최단 경로를 찾는 문제다익스트라로 문제를 해결하기 위해서는 정점 수 만큼 반복해야 함: O(n^3)간단히 플로이드 알고리즘으로 부르기도 함플로이드 알고리즘의 시간 복잡도는 O(n
18.[알고리즘1] 동적계획_0-1 배낭 문제
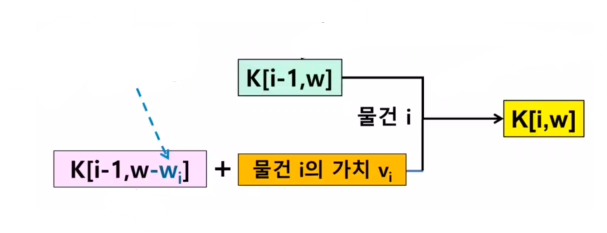
이전에 푼 문제에서 물건을 나누지 않고 1개 단위로 담을 수 있음문제의 요소: 물건, 물건의 무게, 물건의 가치, 배낭의 용량물건과 물건의 무게를 사용K\[i, w] = 물건 1~i까지만 고려하고, 임시 배낭 용량이 w일 때의 최대가치문제의 최적 해: K=\[n, C]
19.[알고리즘1] 동적계획_동전 거스름돈 문제

그리디에서 해결되지 않는 문제가 있었다. 하지만 DP 알고리즘은 모든 동전 거스름돈 문제에 대해 항상 최적해를 찾을 수 있다.문제의 입력요소: 동전의 종류, 거스름돈 n원거스름돈을 1원씩 증가시키며 문제를 해결1차원 배열 C로 표현점화식C\[j] = min{C\[j-d
20.[알고리즘1] 동적계획_편집 거리

삽입, 삭제, 대체 연산으로 스트링 S를 수정하여 다른 스트링 T로 변환하고자 할 때 필요한 최소으 편집 연산 횟수접두부를 고려예제strong을 stone으로 변화는ㄴ 문제에 대해, stro를 sto로 바꾸는 편집 거리를 미리 알면, ng를 ne로 바꾸는 편집 거리를
21.[알고리즘1] 동적계획_연속 행렬 곱셈
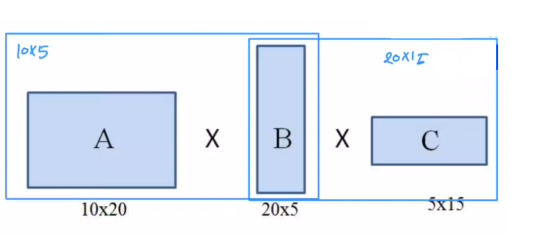
연속된 행렬들의 곱셈에 필요한 원소 간의 곱셈 횟수를 최소로 하는 최적의 곱셈 순서를 찾는 문제행렬의 곱셈의 특성 중 결합법칙을 고려하는 것C\[i,j]: A_i에서 A_j까지 연속적으로 곱하는 데 필요한 곱셈 연산의 최소 횟수점화식C\[i,j] = min(C\[i,
22.[알고리즘1] 정렬 알고리즘_버블정렬
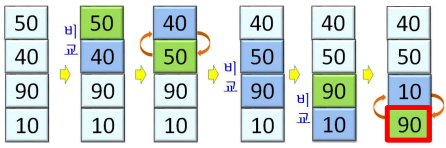
이웃하는 숫자를 비교하여 작은 수를 앞으로 이동시키는 과정을 반복하여 정렬작은 수는 배열의 앞부분으로 이동하는데, 배열을 좌우가 아니라 상하로 그려보면 정렬하는 과정에서 작은 수가 마치 거품처럼 위로 올라가는 것을 연상케함패스(pass): 입력된 배열의 전체 요소를 1
23.[알고리즘1] 정렬 알고리즘_쉘 정렬
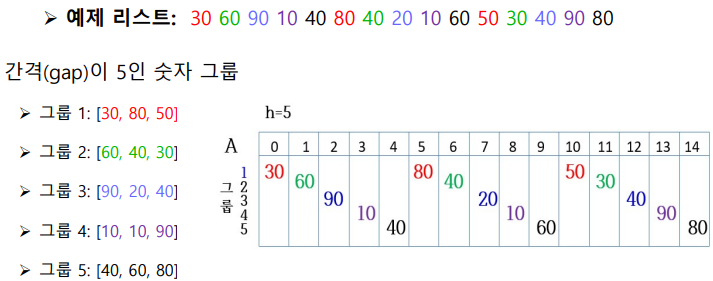
삽입/선택/버블 정렬 알고리즘은 모든 다른 숫자들이 1칸 씩 이동해야 함삽입 정렬을 이용해 배열 뒷부분의 작은 숫자를 앞부분으로 빠르게 이동시키고, 동시에 앞부분의 큰숫자는 뒷부분으로 빠르게 이동간격의 크기만큼 숫자들을 그룹으로 나눔그룹별로 삽입 정렬을 수행간격의 크기
24.[알고리즘1] 정렬 알고리즘_힙 정렬
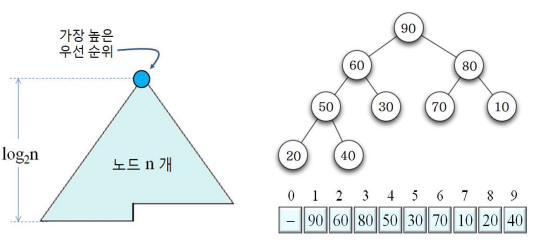
이진힙에 원소를 추가한 뒤 하나씩 꺼내어 정렬힙 조건을 만족하는 완전이진트리(Complete Binary Tree)힙의 조건: 각 노드의 우선 순위가 자식 노드의 우선 순위보다 높음최대 힙: 가장 큰 값이 루트 노드에 저장최소 힙: 가장 작은 값이 루트 노드에 저장주로
25.[알고리즘1] 정렬 알고리즘_기수 정렬
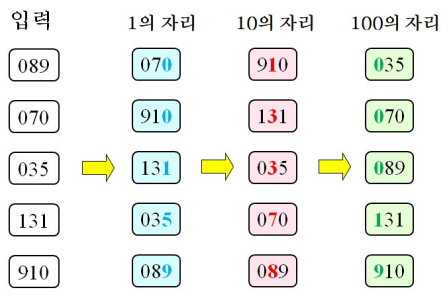
숫자를 부분적으로 비교하며 정렬하는 알고리즘기(radix)는 특정 진수를 나타내는 숫자들을 의미10진수의 기: 0, 1, 2, ..., 92진수의 기: 0, 1기수 정렬은 제한적인 범위 내에 있는 숫자에 대해 각 자릿수별로 정렬을 수행하는 알고리즘RadixSort는 1
26.[알고리즘1] 정렬 알고리즘_정렬 알고리즘의 하한
비교 정렬: 숫자대 숫자로 정렬이 되는 알고리즘정렬 문제의 하한(lower bound): 어떤한 알고리즘이더라도 문제의 하한보다 빠르게 해를 구할 수 없음어떠한 알고리즘일지라도 해를 찾기 위해서 적어도 하한의 시간복잡도만큼의 시간이 걸림알고리즘의 하한을 뜻하는 것이 아
27.[알고리즘1] 정렬 알고리즘_외부 정렬
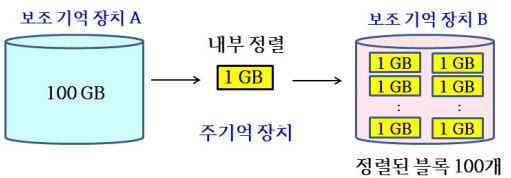
내부정렬: 입력이 주기억 장치(내부 메모리)에 있는 상태에서 정렬이 수행되는 정렬외부정렬입력 크기가 매우 커서 읽고 쓰는 시간이 오래 걸리는 보조 기억 장치에 입력을 저장할 수밖에 없는 상태에서 수행되는 정렬주기억 장치의 용량이 1GB이고, 입력 크기가 100GB라면,
28.[알고리즘1] 정렬 알고리즘_2-way 합병
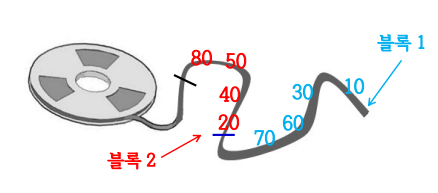
ExternalSort 알고리즘에서는 하나의 보조 기억 장치에서 2개의 블록을 동시에 주기억 장치로 읽어 들일 수 있다는 가정2개의 블록이 각각 다른 보조 기억 장치에서 읽어 들여야하는 경우도 있음테이프 드라이브(Tape Drive) 저장 장치는 블록을 순차적으로만 읽
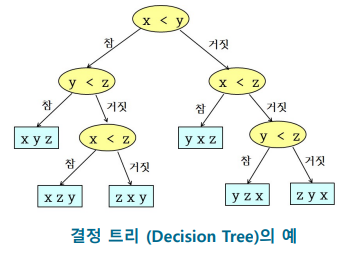
29.[알고리즘1] 백트래킹

해를 탐색하는 도중 막히면 되돌아가서 다시 해를 탐색\-최적화(optimization)문제와 결정(decision)문제를 해결하는 데 유용하게 활용결정(decision)문제: 문제의 조건을 만족하는 해가 존재하는 지의 여부를 yes 또는 no로 답시작 노드: A, to
30.[휴리스틱] 휴리스틱 알고리즘(Heuristic Algorithm)
불충분한 시간이나 정보로 인하여 합리적인 판단을 할 수 없거나, 체계적이면서 합리적인 판단이 굳이 필요하지 않은 상황에서 사람들이 빠르게 사용할 수 있게 보다 용이하게 구성된 간편 추론의 방법기본적으로 모두 최적해가 될 가능성이 없는 답들을 탐색하는 것을 방지해 탐색할
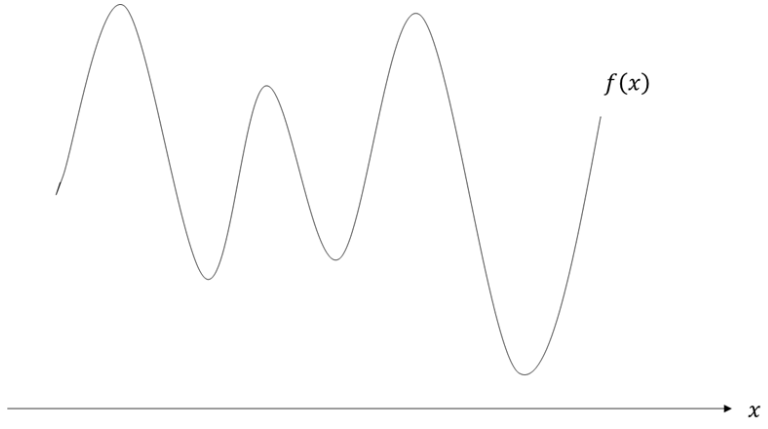
31.[휴리스틱] A* 알고리즘
A* 알고리즘 그래프/트리의 탐색 알고리즘으로 길찾기 알고리즘이다. 게임에서 많이 사용되며 다익스트라의 확장판, BFS의 가지치기 알고리즘이라 생각하면 된다. 따라서 휴리스틱 알고리즘이기도 하다. 1. 휴리스틱 추정값 f(x) = h(x) + g(x) f(x):
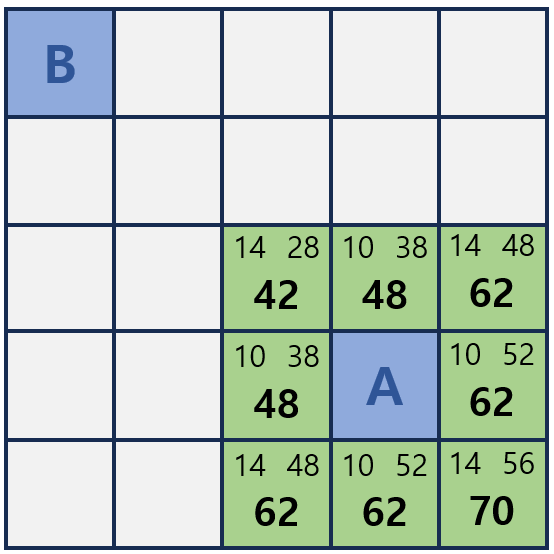
32.[알고리즘] 프림 알고리즘

프림 알고리즘은 최소 신장 트리(Minimum Spanning Tree, MST)를 찾는 알고리즘 중 하나입니다. 최소 신장 트리란, 하나의 그래프에서 모든 정점을 포함하면서 그래프의 간선 가중치의 합이 최소가 되는 트리를 말합니다.프림 알고리즘은 그리디 알고리즘의 일
33.[알고리즘] 깊이 우선 탐색(DPS)과 너비 우선 탐색(BFS)
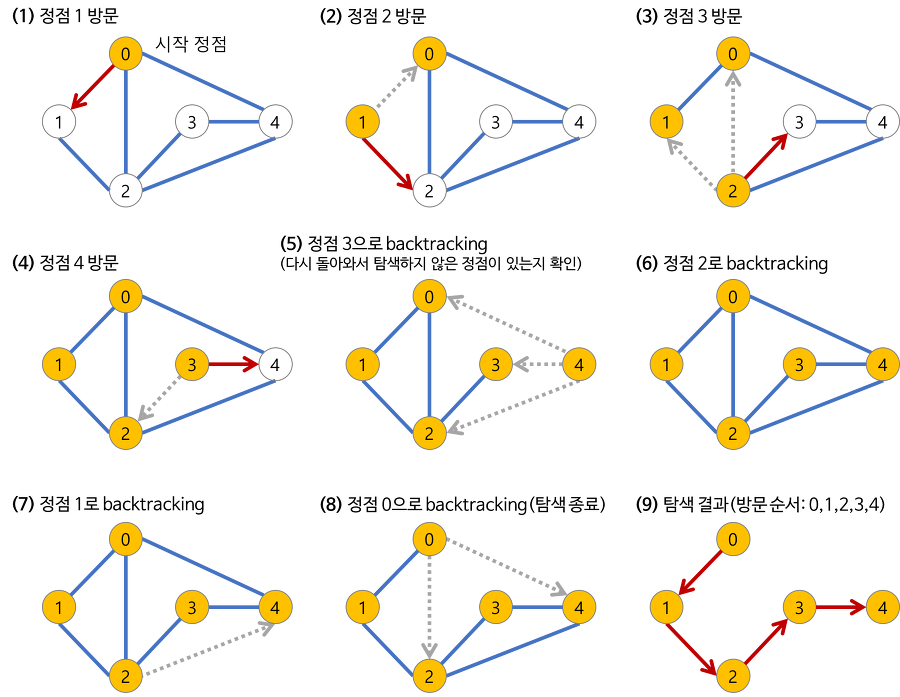
: 하나의 정점으로부터 시작하여 차례대로 모든 정점들을 한 번씩 방문하는 것 : 루트 노드에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법모든 노드를 방문하고자 하는 경우에 이 방법을 선택함깊이 우선 탐색이 너비 우선 탐색보다 좀 더 간
34.[알고리즘] 크루스칼(Kruskal)

1. 크루스칼 알고리즘 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘 최소 비용 신장 트리를 만들기 위한 대표적인 알고리즘 여러개 도시가 있을 때 각 도시를 도로로 연결하기 위한 최소비용을 구할 수 있음 2. 용어 정리 노드 = 정점 = 도시: 그래
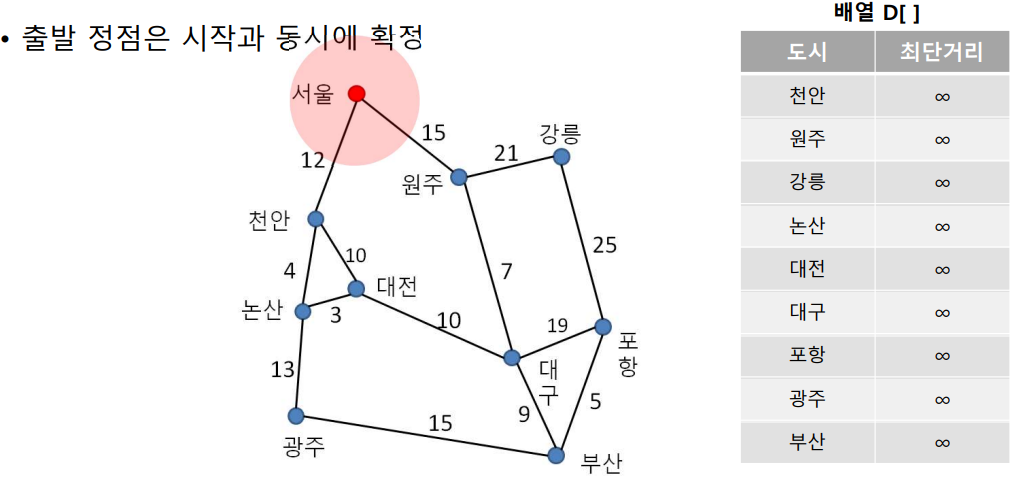
35.[알고리즘] 다익스트라 알고리즘

다이나믹 프로그래밍을 활용한 대표적인 최단 경로 탐색 알고리즘특정한 하나의 정점에서 모든 정점으로 가는 최단 경로를 알려줌음의 간선을 포함할 수 없음하나의 최단 거리를 구할 때 그 이전까지 구했던 최단 거리 정보를 그대로 사용적용 과정1) 출발 노드를 설정2) 출발 노
36.[알고리즘]위상 정렬
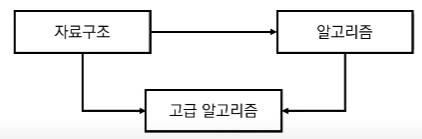
사이클이 없는 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것을 의미예시) 선수과목을 고려한 학습순서 설정세 과목을 듣기 위해선 자료구조->알고리즘->고급알고리즘 순진입차수(Indegree): 특정한 노드로 들어오는 간선의 개수진출차수(Outd
37.[알고리즘] 쿼드트리(Quad tree)
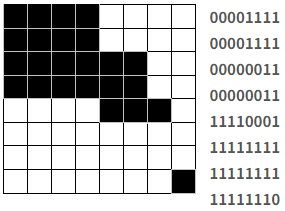
트리 자료구조 중 하나로 부모 노드 아래에 자식 노드를 4개씩 가지고 있음이미지 용량, 충돌, 컬링 등 다양한 곳에서 최적화 기법으로 사용쿼드 트리를 사용해 흑백 이미지를 압축해보자(0(1101)1((0011)(0111)1(1110)))이미지의 구역을 4개로 나눈 후,
38.[알고리즘] BSP (Binary Space Partitioning)
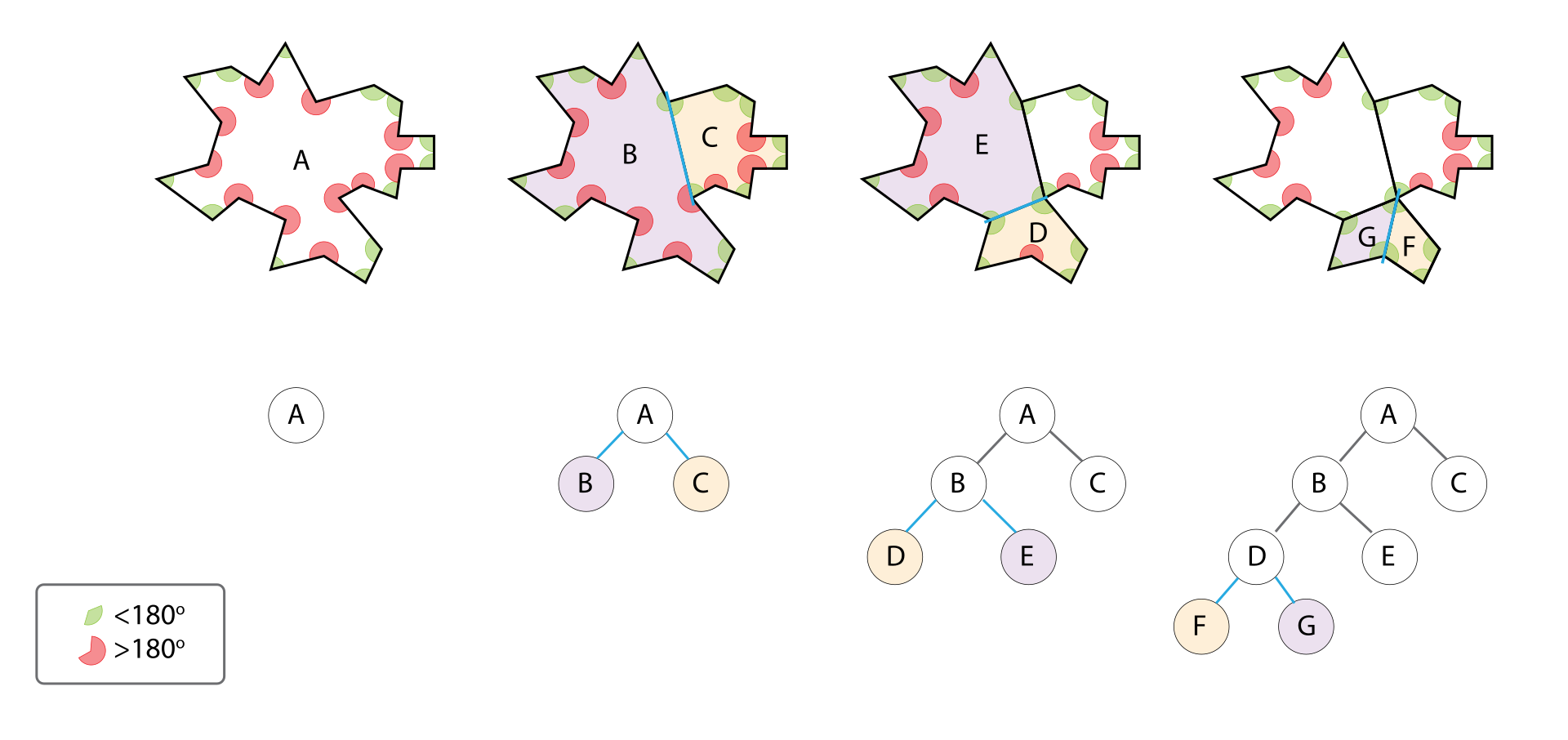
재귀적으로 유클리드 공간을 초평면상의 볼록 집합으로 분할하는 알고리즘하나의 공간을 두 개씩 나누어 가는 과정을 재귀적으로 실행맵 렌더링, 충돌 감지 등에 최적화를 위해 사용하나의 분할 평면을 선택하나의 분할 평면을 두 개의 하위 공간으로 분할각 하위 공간에 대해 1~2