연속 행렬 곱셈 문제

연속된 행렬들의 곱셈에 필요한 원소 간의 곱셈 횟수를 최소로 하는 최적의 곱셈 순서를 찾는 문제

행렬의 곱셈의 특성 중 결합법칙을 고려하는 것

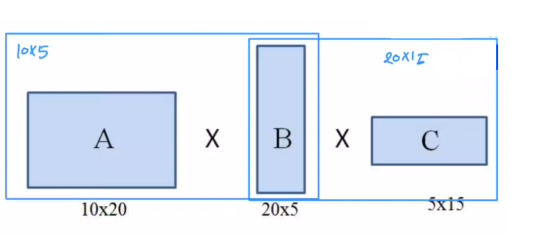
1. 부분 문제 정의

• C[i,j]: A_i에서 A_j까지 연속적으로 곱하는 데 필요한 곱셈 연산의 최소 횟수

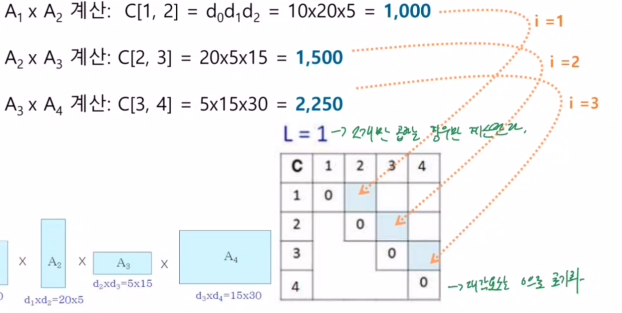
• 점화식
  C[i,j] = min(C[i, k]+C[k+1,j]+d_i-1d_kd_j)

2. 알고리즘

/////////초기화//////////
for i=1 to n
  C[i,i] = 0
  
for L=1 to n-1
  for i=1 to n-L
    j = i+L;
    C[i,j] = infinite
    for k=i to j-1
      temp = C[i,k] + C[k+1, j] + d_i+1*d_k*d_j
      if(temp < C[i,j])
        C[i,j] = temp;

3. 시간복잡도

• 총 부분 문제 수: (n-1) + (n-2) +...+ 2+ 1 = n(n-1)/2
• 하나의 부분 문제에 대해, k-루프가 최대 (n-1)번 수행
• 따라서 시간 복잡도는 O(n^2)xO(n) = O(n^3)