1. 알고리즘이란

• 문제를 해결하는 단걔적 절차 또는 방법

1.1. 알고리즘의 일반적 특성

• 정확성: 알고리즘은 주어진 입력에 대해 올바른 해를 도출해야 함
• 수행성: 알고리즘의 각 단계는 컴퓨터에서 수행 가능해야 함
• 유한성: 알고리즘은 유한 시간 내에 종료 되어야 함
• 효율성: 알고리즘은 효율적일 수록 가치가 높아짐

2. 최초의 알고리즘

• 유클리드의 최대공약수 알고리즘
  • 기원전 300년경에 만들어진 가장 오래된 알고리즘
  • 유클리드 알고리즘, 유클리드 호제법이라고도 불림
  • 최대공약수란 두 자연수의 공약수들 중에서 가장 큰 수를 의미함
  • 2개의 자연수의 최대공약수는 큰 수에서 작은 수를 뺀 수와 작은 수와의 최대공약수와 같다
  • 뺄셈 대신 나눗셈을 이용하면 더 빠르게 해를 찾을 수 있음

  Euclid(a,b):
    1. if b==0 return a
    2. return Euclid(b,a mod b)

3. 알고리즘의 표현법

3.1. pseudo code

• 이유: 가독성, 간결성, 정확성
• 의사코드는 프로그래밍 언어 형태와 유사하되, 각 단계별 기능을 모호성 없이 명확하게 표현할 수 있도록 간결해야 함

3.2. 자연어

3.3. 플로우차트

4. 알고리즘의 효율성을 표현하는 방법

• 수행시간과 사용되는 메모리 크기로 표현 가능
• 시간복잡도
• 공간복잡도

4.1. 시간복잡도

알고리즘이 실행되는 동안 사용된 기본 연산의 횟수를 입력 크기에 대한 함수로 나타냄

• 분석방법
  • 최악의 경우 분석: 상한의 의미로 분석
  • 평균의 경우 분석: 일반적으로 균등 분포를 가정
  • 최선의 경우 분석: 가장 빠른 수행시간을 분석해, 최적의 알고리즘을 찾는데 활용
  • 상각 분석: 일련의 연산을 수행 후 총 수행시간을 합해 이를 연산횟수로 나누어 분석
    • 적어도 두 종료의 연산이 일어나며, 하나는 길고 다른하나는 짧으며 수행시간이 긴 연산은 적게 짧은 수행시간을 가진건 많이 수행되어야 의미를 가짐

일반적으로 최악의 경우 분석으로 표현

5. 시간복잡도의 점근적 표기 방법

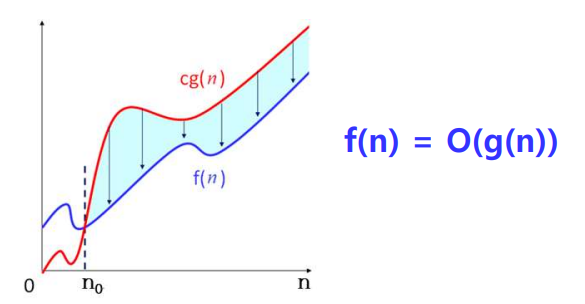
5.1. O(Big-Oh)표기

• O표기의 정의: 모든 n>=n0에 대해 f(n)<=cg(n)이 성립하는 양의 상수와 c와 n0가 존재하면, f(n) = O(g(n))
• O표기의 의미
  • n0와 같거나 큰 모든 n에 대해 f(n)이 cg(n)보다 크지 않다는 것
  • f(n) = O(g(n))은 n0보다 큰 모든 n에 대해 f(n)이 양의 상수를 곱한 g(n)에 미치지 못한다는 뜻
• g(n)을 f(n)의 상한이라 함
  

5.2. Ω(Big-Omega)표기

• Ω-표기의 정의: 모든 n ≥ n0에 대해서 f(n) ≥ cg(n)이 성립하는 양의 상수 c와 n0가 존재하면, f(n) = Ω(g(n))이다
• Ω-표기의 의미
  • n0 보다 큰 모든 n 대해서 f(n)이 cg(n)보다 작지 않다는 것
  • f(n) = Ω(g(n))은 양의 상수를 곱한 g(n)이 f(n)에 미치지 못한다는 뜻
• g(n)을 f(n)의 하한(Lower Bound)이라고 한다.
  

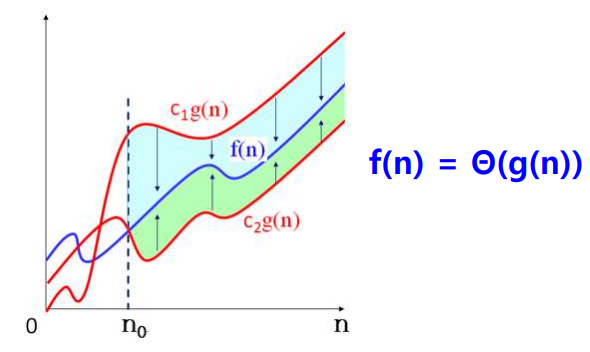
5.3. θ(Theta)표기

• Θ-표기의 정의: 모든 n ≥ n0에 대해서 c1g(n) ≥ f(n) ≥ c2g(n)이 성립하는 양의 상수 c1
  , c2, n0가 존재하면, f(n) = Θ(g(n))
• Θ-표기의 의미: 수행시간의 O-표기와 Ω-표기가 동일한 경우에 사용한다. 즉 동일한 증가율을 의미
• Θ(n2)은 n2과 (2n2+3n+5)이 유사한 증가율을 가지고 있다는 뜻