1. 문제의 하한

• 비교 정렬: 숫자대 숫자로 정렬이 되는 알고리즘
• 정렬 문제의 하한(lower bound): 어떤한 알고리즘이더라도 문제의 하한보다 빠르게 해를 구할 수 없음
  • 어떠한 알고리즘일지라도 해를 찾기 위해서 적어도 하한의 시간복잡도만큼의 시간이 걸림
  • 알고리즘의 하한을 뜻하는 것이 아님

2. 최댓값 찾는 문제의 하한

• 최댓값을 찾기 위해선 적어도 n-1번의 비교가 필요
• n-1보다 적게 비교해서는 최댓값을 항상 찾을 수 없음

3. 정렬 문제의 하한

• 3개의 서로다른 숫자 x,y,z에 대해, 정렬에 필요한 모든 경우의 숫자 대 숫자 비교
  
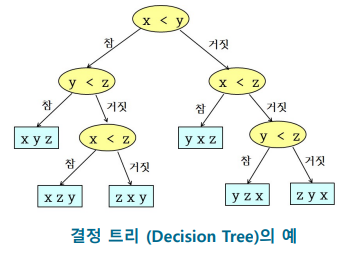
• 각 내부 노드에서는 2개의 숫자가 비교됨
• 비교 결과가 참이면 왼쪽으로 거짓이면 오른쪽으로 분기됨
• 각 리프노드에는 정렬된 결과가 저장됨

3.1. 결정 트리의 특징

• 단말노드의 수: (비교하는 숫자의 수)!
  • 3! = 6
• 결정 트리는 이진트리(binary tree)
• 결정 트리에는 정렬을 하는데 불필요한 내부 노드가 없음
  • 중복 비교는 있으나, 이들은 루트로부터 각 단말 노드의 정렬된 결과를 얻기 위해 반드시 필요한 노드

3.2. 결정 트리의 비교

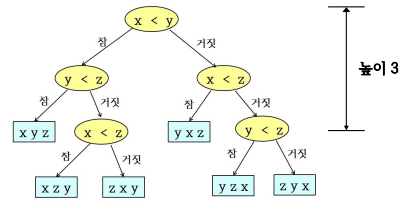
• 어느 경우에도 서로 다른 3개의 숫자가 정렬되기 위해서는 적어도 3번의 비교가 필요
  • 3번: 결정트리의 높이
    

3.3. 시간복잡도

• n!개의 단말 노드를 가진결정 트리의 높이는 log(n!)보다 큼
• log(n!) = O(nlogn)이므로, 비교 정렬의 하한의 O(nlogn)