힙 정렬

• 이진힙에 원소를 추가한 뒤 하나씩 꺼내어 정렬

1.이진 힙

1.1. 개념

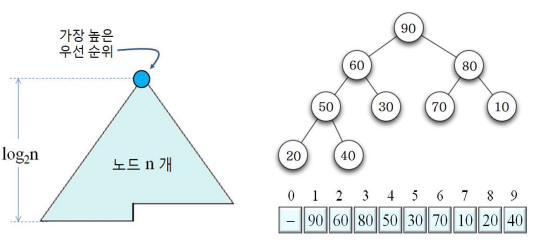
• 힙 조건을 만족하는 완전이진트리(Complete Binary Tree)
• 힙의 조건: 각 노드의 우선 순위가 자식 노드의 우선 순위보다 높음
• 최대 힙: 가장 큰 값이 루트 노드에 저장
• 최소 힙: 가장 작은 값이 루트 노드에 저장

1.2. 구현

• 주로 노드들을 빈 공간없이 배열에 저장
• 힙에서 부모 노드와 자식 노드의 관계
  • A[i]의 부모 = A[i/2]
  • A[i]의 왼쪽 자식 = A[2i]
  • A[i]의 오른쪽 자식 = A[2i+1]

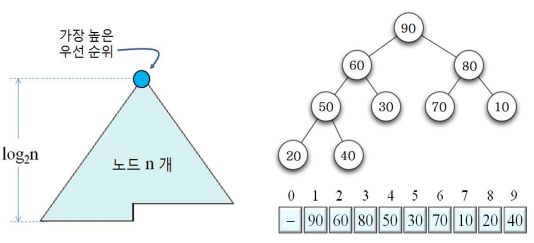
2. 힙 정렬 과정

• 정렬할 입력 리스트로부터 최대 힙을 만듦
• 힙의 루트에 가장 큰 수 가 있으므로, 루트와 힙의 가장 마지막 노드를 교환
  • 가장 큰 수를 배열의 맨 뒤로 옮김
• 힙의 크기를 1 감소시킴
• 루트에 새로 저장된 숫자로 입해 위배된 힙 조건이 있는지 확인하고, 이를 해결하여 힙의 조건을 만족시킴
• 상기 과정을 반복하여 정렬을 완료

3. 소스코드

heapSize = n
for i=1 to n-1
  Swap(A[1], A[heapSize])
  heapSize -= 1
  DownHeap()
return A

4. 시간복잡도

• 힙 자료구조 만드는 시간: O(n)
• for 내에서 DownHeap()을 제외한 나머리 명령 수행 시간: O(1)
• for 내에서 DownHeap()의 수행 시간: O(nlogn)
• 최종 시간: O(n)+O(1)+O(nlogn) = O(nlogn)