[AL] 카데인 알고리즘 - JavaScript

LeetCode 문제를 풀다가 배열에서 최대 합을 가지는 연속된 부분배열을 구하는 문제를 풀게 되었는데 처음엔 Brute Force 방법으로 for문을 중첩하여 풀어보려다가 최대 부분합 문제에는 Kadane's Algorithm (카데인 알고리즘)을 사용한다는 글을 보고 알고리즘을 찾아보았고 이해하기 쉽게 정리해보자🏃‍♂️

카데인 알고리즘 (Kadane's Algorithm)

카데인 알고리즘은 DP (Dynamic Programing)의 기법중 하나인데 DP를 간단하게 설명하자면 다음과 같다.

Dynamic Programing : 하나의 큰 문제를 풀기위해 그 문제를 작은 문제들로 나눠 풀어나간 후, 결국 하나의 큰 문제를 풀어내는 방법이다.

카데인 알고리즘은 최대 부분합 문제를 풀때 주로 사용되기 때문에 문제를 보며 설명해보자!

최대 부분합 문제

Arr = [-2,1,-3,4,-1,2,1,-5,4];

다음과 같은 배열이 주어질 때 위의 순서를 유지하고, 연속적이면서 가장 큰 합을 가지는 부분배열은 다음과 같다.

[4, -1, 2, 1] -> 합 : 6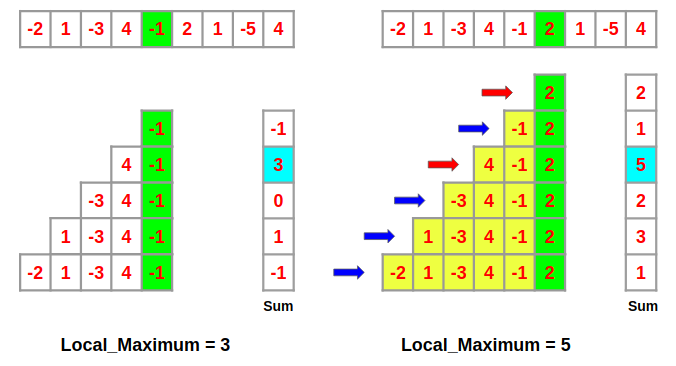

Arr[4] = -1 를 마지막 원소로 갖는 부분 합과, Arr[5] = 2를 마지막 원소로 갖는 부분 합을 구하는 과정을 과정을 확인해보면 위와 같이 나타나게 된다.

위 과정을 통해 발견할 수 있는 규칙은 Arr[4]의 부분합 + Arr[5] 을 통해 Arr[5]의 부분 합을 구할 수 있기 때문에 Arr[5]의 부분합을 구할때 앞의 합들을 따로 구할 필요 없이 Arr[4]의 부분 합을 알고 있기 때문에 바로 구할수가 있는 것이다.

이 규칙을 통해 점화식을 구하게 된다면 다음과 같다.

최대 부분합[i] = max(Arr[i-1]의 부분 합 + Arr[i] , Arr[i])

만약 Arr[4]의 부분합 + Arr[5] 보다 Arr[5]의 값이 독자적으로 크다면, Arr[5]부터 시작하는 부분 배열로 다시 계산하게 되는 것이다.

코드

위의 문제를 코드로 풀어내면 다음과 같이 나타낼 수 있다.

const maxSubArray = (nums) => {
    // 배열의 길이가 1이면 그 자체로 이미 최대 부분합
    if(nums.length === 1) return nums[0];
    
    for(let i=1; i<nums.length; i++){
        nums[i] = Math.max(nums[i], nums[i]+nums[i-1]);
    }
    
    return Math.max(...nums);
};

참고자료
참고자료