[AL] 투 포인터 알고리즘 (+슬라이딩 윈도우) - JavaScript

일차원 배열이 주어졌을 때 연속된 구간의 합이 M이 되도록 하는 경우의 수를 구하는 문제가 주어진다면 가장 먼저 생각 하는 방법은 바로 이중 for문을 이용하는 방법이다.

function solution() {
  const arr = [1,3,2,2,5,7,2,6];
  const M = 9;
  let ans = 0;
  
  for(let i=0; i<arr.length; i++){  // 연속된 구간의 시작
  	let sum = arr[i];
    for(let j=i+1; j<arr.length; j++){
    	if(sum === M) ans++;
      	else if(sum > M) break;
      	else sum += arr[j];
    }
  }
  return ans;
}

위와 같은 방법으로 이중 for문을 이용하면 시간 복잡도가 $O(N^2)$ 이므로 배열의 크기가 커질수록 엄청 느려지게 될 것이다.. 🙄

이러한 이중 for문의 느림을 보완하기 위해서 나온 알고리즘이 바로 오늘 다룰 투 포인터(Two Pointers) 알고리즘이다!

투 포인터 알고리즘 (Two Pointers Algorithm)

투 포인터 알고리즘 (Two Pointers Algorithm)은 일차원 배열에서 두 개의 포인터의 위치를 기록하면서 처리하는 알고리즘을 의미한다.

위에서 다뤘던 예시를 가지고 투 포인터 알고리즘을 이해해보자!

알고리즘 설명

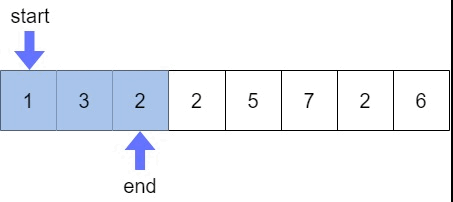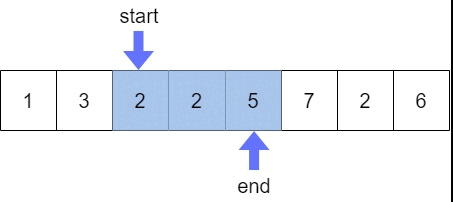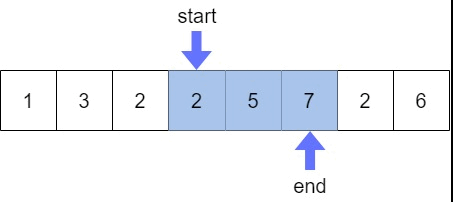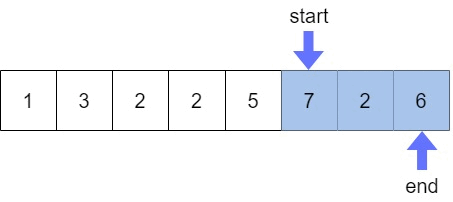
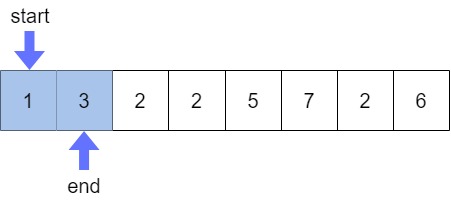
첫번째로 start, end 두개의 포인터가 배열의 0번째 원소를 가리키게 한다.

🔑 Key Point 🔑
만약 현재 구간의 합이 M(9)와 같다면 ans 값을 증가시켜주고 합이 M(9) 보다 작거나 같다면 end를 1 증가시켜주고, 합이 M(9) 보다 크다면 start를 1 증가시킨다.

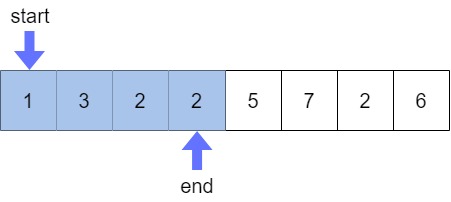
위의 Key Point를 계속 적용하다보면 구간의 합이 8이 될때까지 위와 같이 end가 이동하게 된다.
여전히 M(9) 보다 작으므로 end를 1 증가시키게 되면 구간의 합이 13이 되므로 start가 1증가되어 아래와 같이 이동하게 된다.

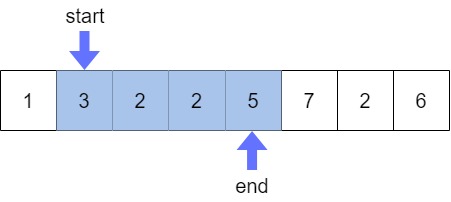
하지만 여전히 구간의 합이 M(9)보다 크므로 start는 또 이동하게 된다.

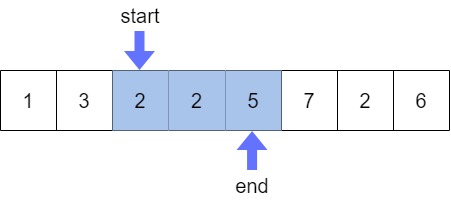
start가 이동하다보면 이렇게 구간의 합이 M(9)와 같아지는데 이때 ans 값을 증가시켜주고 end 1 증가시켜주면 된다. 이를 코드로 나타내면 아래와 같다.

function solution() {
  const arr = [1,3,2,2,5,7,2,6];
  const M = 9;
  let ans = 0;
  let start = 0, end = 0, sum = arr[0];
  
  while(arr[start] && arr[end]){
    if(sum === M){
      ans++;
      end++;
      sum += arr[end];
    }else if(sum > M){
      sum -= arr[start];
      start++;
    }else{
      end++;
      sum += arr[end];
    }
  }
  return ans;
}

슬라이딩 윈도우 알고리즘 (Sliding Window Algorithm)

슬라이딩 윈도우 알고리즘 (Sliding Window Algorithm) 은 투 포인터 알고리즘과 매우 비슷한 개념을 가지고 있다.
투 포인터의 경우에는 두 개의 포인터가 각각 움직이지만,
슬라이딩 윈도우의 경우에는 일정한 사이즈를 가지는 윈도우를 나타내는 처음과 끝 포인터가 함께 움직인다.

만약 위에서 다뤘던 예제를 가지고 슬라이딩 윈도우를 나타낸다면 아래와 같이 움직일 것이다.
(윈도우의 사이즈는 3이라고 가정하고)

참고 자료
참고 자료