
하나의 정점을 출발점으로 지정하여 모든 정점까지의 최단 거리를 구하는 다익스트라 알고리즘,
모든 정점들을 출발점으로 지정하여 모든 정점까지의 최단 거리를 구하는 플로이드 와샬 알고리즘이 최단 거리를 구할때 주로 쓰이는 알고리즘이다.
오늘은 이 둘중에서 플로이드 와샬 알고리즘에 대해서 다뤄 보자🏃♂️
플로이드 와샬 알고리즘 (Floyd-Warshall Algorithm)
플로이드 와샬 알고리즘 (Floyd-Warshall Algorithm)은 위에서 언급했다싶이,
모든 각각의 정점들을 출발점으로 지정하고 다른 모든 정점까지의 최단거리(경로)를 구하는 알고리즘이다.
🔥플로이드 와샬 알고리즘의 가장 중요한 키포인트는 시작 정점과 최종 정점 사이에 거쳐가는 중간 정점을 기준으로 알고리즘을 수행한다는 것이다.🔥
또한 기본적으로 DP(동적 프로그래밍)에 의거하는 알고리즘이다.
⚡ Dynamic Programing : 하나의 큰 문제를 풀기위해 그 문제를 작은 문제들로 나눠 풀어나간 후, 결국 하나의 큰 문제를 풀어내는 방법이다.
알고리즘 설명
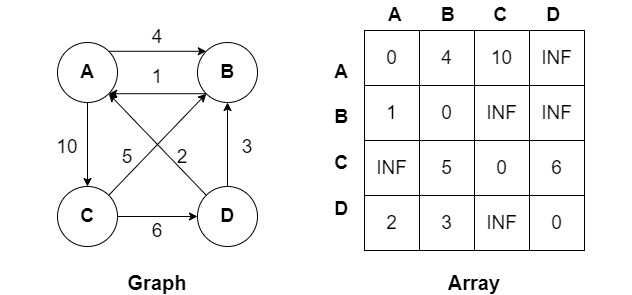
위 그래프는 각 정점 사이의 거리 비용(가중치)를 표현한 것이고, 그 옆은 해당 가중치들을 배열을 이용하여 표현한 것이다.
-
A를 시작 정점으로 설정하고, A를 중간 정점으로 설정한다. 이때 A에 인접한 정점, 즉 A에서 갈 수 있는 정점은 B, C이다. 이 정보를 가지고 A의 경로를 나타내면 다음과 같다.
A(시작 정점) -> A(중간 정점) -> B(최종 정점) : 이동거리 4
A(시작 정점) -> A(중간 정점) -> C(최종 정점) : 이동거리 10 -
B를 시작 정점으로 설정하고, A를 중간 정점으로 설정한다. 이때 B에 인접한 정점은 A이다. 이 정보를 가지고 B의 경로를 나타내면 다음과 같다.
B(시작 정점) -> A(중간 정점) -> A(최종 정점) : 이동거리 1
-
C를 시작 정점으로 설정하고, A를 중간 정점으로 설정한다. 이때 C에 인접한 정점은 B, D이다. 이 정보를 가지고 C의 경로를 나타내면 다음과 같다.
C(시작 정점) -> A(중간 정점) -> B(최종 정점) : 이동거리 INF
C(시작 정점) -> A(중간 정점) -> D(최종 정점) : 이동거리 INF
이 경우에는 C->A->B (INF) 보다 C->B (5)와, C->A->D (INF) 보다 C->D (6)이 더 적은 거리를 이동하므로 값이 바뀌지 않는다.
- D를 시작 정점으로 설정하고, A를 중간 정점으로 설정한다. 이때 D에 인접한 정점은 A, B이다. 이 정보를 가지고 D의 경로를 나타내면 다음과 같다.
D(시작 정점) -> A(중간 정점) -> A(최종 정점) : 이동거리 2
D(시작 정점) -> A(중간 정점) -> B(최종 정점) : 이동거리 6
이 경우에는 D->A->B (6) 보다 D->B (3)이 더 적은 거리를 이동하므로 값이 바뀌지 않는다.
이런식으로 중간 정점을 A~D까지 모든 경우의 값을 설정하여
dist[시작 정점][최종 정점] > dist[시작 정점][중간 정점] + dist[최종정점][중간 정점]
위와같은 조건식을 이용해서 가중치 값을 더 작은 값으로 업데이트 시켜주는 과정을 반복하면 모든 각각의 경로에 대한 최단 경로 값을 구할 수 있게 된다.
예시 문제
문제 설명
n명의 권투선수가 권투 대회에 참여했고 각각 1번부터 n번까지 번호를 받았습니다. 권투 경기는 1대1 방식으로 진행이 되고, 만약 A 선수가 B 선수보다 실력이 좋다면 A 선수는 B 선수를 항상 이깁니다. 심판은 주어진 경기 결과를 가지고 선수들의 순위를 매기려 합니다. 하지만 몇몇 경기 결과를 분실하여 정확하게 순위를 매길 수 없습니다.
선수의 수 n, 경기 결과를 담은 2차원 배열 results가 매개변수로 주어질 때 정확하게 순위를 매길 수 있는 선수의 수를 return 하도록 solution 함수를 작성해주세요.
제한 사항
- 선수의 수는 1명 이상 100명 이하입니다.
- 경기 결과는 1개 이상 4,500개 이하입니다.
- results 배열 각 행 [A, B]는 A 선수가 B 선수를 이겼다는 의미입니다.
- 모든 경기 결과에는 모순이 없습니다.
입출력 예
n results return 5 [[4, 3], [4, 2], [3, 2], [1, 2], [2, 5]] 2
입출력 예 설명
2번 선수는 [1, 3, 4] 선수에게 패배했고 5번 선수에게 승리했기 때문에 4위입니다.
5번 선수는 4위인 2번 선수에게 패배했기 때문에 5위입니다.
문제 풀이
먼저 주어진 results값들을 이용해서 각 정점 사이, 즉 선수들 사이에 경기가 이루어졌는지 여부와 만약 경기가 이루어진 경우라면 누가 이겼는지에 대한 정보를 이차원 배열에 넣어줘야 한다.
const graph = new Array(n+1);
for(let i=0; i<graph.length; i++){
graph[i] = new Array(n+1).fill(false);
}
results.forEach((v)=>{
const [A,B] = v;
graph[A][B] = 1;
graph[B][A] = -1;
graph[A][A] = 0;
graph[B][B] = 0;
});n+1 X n+1 사이즈를 가지는 배열에 false 값을 채워서 준비 한 다음, results 값들을 기준으로
A 선수와 B 선수 사이의 경기 여부 및 결과 = graph[A][B] 이런식으로 값을 넣어 준다.
A 선수가 B 선수를 이긴 경우에는 1, A 선수가 B 선수에게 진 경우에는 -1, 둘 사이의 경기가 없었다면 false 값만 남아있게 될 것이다. (자기 자신에서 자기 자신에게 가는 경우는 0으로 값을 입력)
for(let pass=0; pass<n+1; pass++){
for(let start=0; start<n+1; start++){
for(let near=0; near<n+1; near++){
// 이기는 경우
if(graph[start][pass] === 1 && graph[pass][near] === 1) graph[start][near] = 1;
// 지는 경우
if(graph[start][pass] === -1 && graph[pass][near] === -1) graph[start][near] = -1;
}
}
}위에서 언급한 플로이드 와샬 알고리즘에 정점대신 선수를 대입하여 코드를 작성하면 다음과 같다.
이 문제는 이기는 경우, 지는 경우 두가지 경우가 있으므로 이를 if문으로 잘 구분하여 나눠주면 된다.
정답 코드
function solution(n, results) {
let answer = 0;
const graph = new Array(n+1);
for(let i=0; i<graph.length; i++){
graph[i] = new Array(n+1).fill(false);
}
results.forEach((v)=>{
const [A,B] = v;
graph[A][B] = 1;
graph[B][A] = -1;
graph[A][A] = 0;
graph[B][B] = 0;
});
for(let pass=0; pass<n+1; pass++){
for(let start=0; start<n+1; start++){
for(let near=0; near<n+1; near++){
// 이기는 경우
if(graph[start][pass] === 1 && graph[pass][near] === 1) graph[start][near] = 1;
// 지는 경우
if(graph[start][pass] === -1 && graph[pass][near] === -1) graph[start][near] = -1;
}
}
}
graph.forEach((line)=>{
if(line.filter((v)=> v === false).length === 1){
answer++;
}
})
return answer;
}