Abstract

• 본 논문에서는 AutoPrune이라는 방법을 제시하며, 이 방법은 원래의 가중치들을 대신하여 학습이 가능한 보조 파라미터들의 최적화를 통해 네트워크를 pruning하는 방법이다.
• 이러한 방식의 장점은 학습 단계에서 발생하거나 개입할 수 있는 노이즈나 불안정성이 본래의 가중치에 직접적으로 영향을 끼칠일이 없어서 pruning 과정이 노이즈에 더 강하며, 강건하다는 점이다. (하이퍼 파라미터에도 덜 민감하다.)
• 이에 더해 gradient 보조 파라미터들의 갱신 방법을 설계하여서 더욱 pruning을 일정하게 할 수 있게 한다.
• 결과적으로 네트워크의 반복을 이전 연구들에서 임곗값에 관한 지식 없이 자동으로 제거할 수 있으며, 실험 단계에서 최적을 위해 실험해보는 시간을 아낄 수 있다.

Methods

Problem Formulation

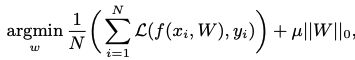
• ||W||_0는 zero norm, 즉 0이 아닌 가중치들의 개수를 뜻한다.
• 여기서 목표는 모델의 정확도를 유지시켜주는 w를 최소로 가져가면서 sparse한 구조를 찾아내는 것이다.
• 하이퍼 파라미터에 너무 민감한 경향을 해결하기 위해서 직접적인 정규화를 하지 않고 아래와 같은 식을 따르는 indicator function을 소개한다.
  
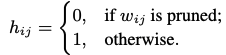
• 매 가중치를 위한 indicator function을 정의하기 보단 보조 파라미터 세트에 대해 일괄적으로 작용할 수 있는 universal한 indicator function M을 정의한다.
• 미분 불가능한 indicator function의 영역으로 인해 문제가 발생한다. 이를 해결하면 아래와 같은 최적화 문제로 re-formulated 될 수 있다.
  
  
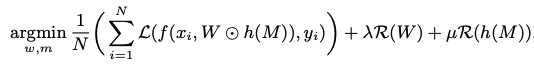
• R()은 정규화 함수를 나타낸다.
  
  
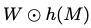
• 위 식은 pruning 후에 원소 간의 연산이며 T로 정의되는 가중치 행렬이다.
• 이렇게 보조 파라미터에 정규화를 진행하는 것은 본래의 가중치들을 건드리지 않아서 좋고, 하이퍼 파라미터인 mu의 영향을 받지 않는 덜 민감한 pruning이 된다는 장점이 있다.
• 이전의 연구들에 의해 안정성과 성능을 향상시키기 위해서 저자들은 sparse한 구조와, 본래의 가중치를 유지시키는 것에 대해 반복적인 다중-단계 학습을 설계한다.
• 조금 더 자세히 들어가면 bi-level optimization 방식을 채택하여 최적화를 한다.
• 데이터셋은 train과 val로 나뉘어지며, single loss function에서 이에 대한 각각의 loss function으로 확장시킨다.
  

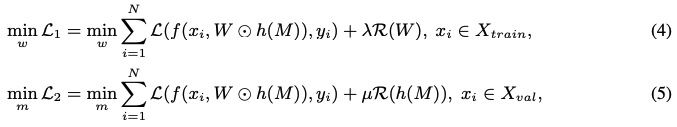
Coarse Gradient for Indicator Function

• h_{ij}는 0과 1만을 값으로 가지기에 불연속 및 미분 불가능하다.
• 이전 연구들에서 binary weight들은 계단 함수와 시그모이드 STE를 사용하여 표현되어 왔지만, indicator function인 h{ij}와 학습가능한 파라미터인 m{ij}를 위해서 저자들은 간단한 계단 함수를 사용한다고 한다.
• 적절한 STE를 가진 BNN(Binary Neural Network)들은 최적화된 이진 파라미터들을 효과적으로 찾아내며, 복잡한 task에서도 좋은 성능을 내는 것으로 잘 알려져있다.
• vanila BNN들은 연속적 변수인 m_{ij}를 계속해서 업데이트하면서 최적화된다.
  

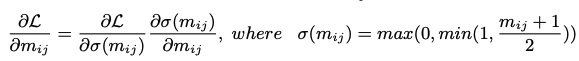
• 각 가중치의 결과들은 각 hard 시그모이드 이진 함수의 출력이 된다.
  

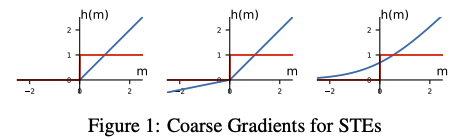
• 보조 파라미터를 정규화 없이 직접적으로 가중치에 적용하면 pruning 하고난 값이 0 이하일때, ReLU에서의 그래디언트가 0으로 값이 영구적으로 죽게되기 때문에 복원성이 있는 pruning을 위해서 저자들은 Leaky ReLU(2)나 Softplus(3)를 사용하는 것을 제시한다.

Updating Auxiliary Parameters

• 직접적으로 gradient 업데이트를 적용하는 것 대신, 저자들은 가중치들의 강도(1), 가중치의 변화(2), BNN gradient의 방향 을 일정하게 하기 위해서 보조 파라미터에 대해 개선된 update 규칙(m_{ij})을 제시한다.

  

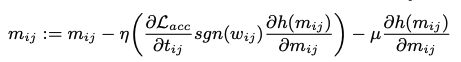
• Sensitivity Consistency:

• Correlation Consistency:

• Direction Consistency:

Recoverable Pruning

• 복원력을 가지고 pruning을 하는 것은 원본 네트워크 그래프와 pruning된 네트워크 그래프 사이의 갭을 최대한 줄이는 것이 중요하다.
• 중요한 가중치를 잘못 pruning 했을 때, loss의 증가를 보상하기 위해서 pruned된 가중치가 다시 살아난다.
• 이전의 정적인 임곗값 대신에 최적화 과정 중에 동적으로 결정하는 임곗값을 사용하여서 model이 더 soft하며, prune 된 가중치가 값을 유지한다.