Abstract
- Diffusion Models (DMs)는 고퀄리티의 이미지를 생성하지만, 수십/수백번의 forward pass를 거쳐야 한다는 단점이 존재한다.
- 본 논문에서는 이미지 품질에 영향을 거의 주지 않으며, 단 한번의 step으로도 이미지 생성을 가능케하는 one-step diffusion을 제시한다.
- 핵심 요건
- KL divergence를 통해 one-step generator와 teacher model의 분포를 비슷하도록 최적화 한다. 이때, gradient는 두 개의 score function의 차로 나타내질 수 있다.
- 간단한 regression loss와의 조합을 통해 기존의 multi-step diffusion의 출력과 one-step generator 간의 출력을 맞춰준다.
- 몇몇의 task에 대해 기존의 DM을 뛰어넘는 성능을 보인다.
Method
3. Distribution Matching Distillation
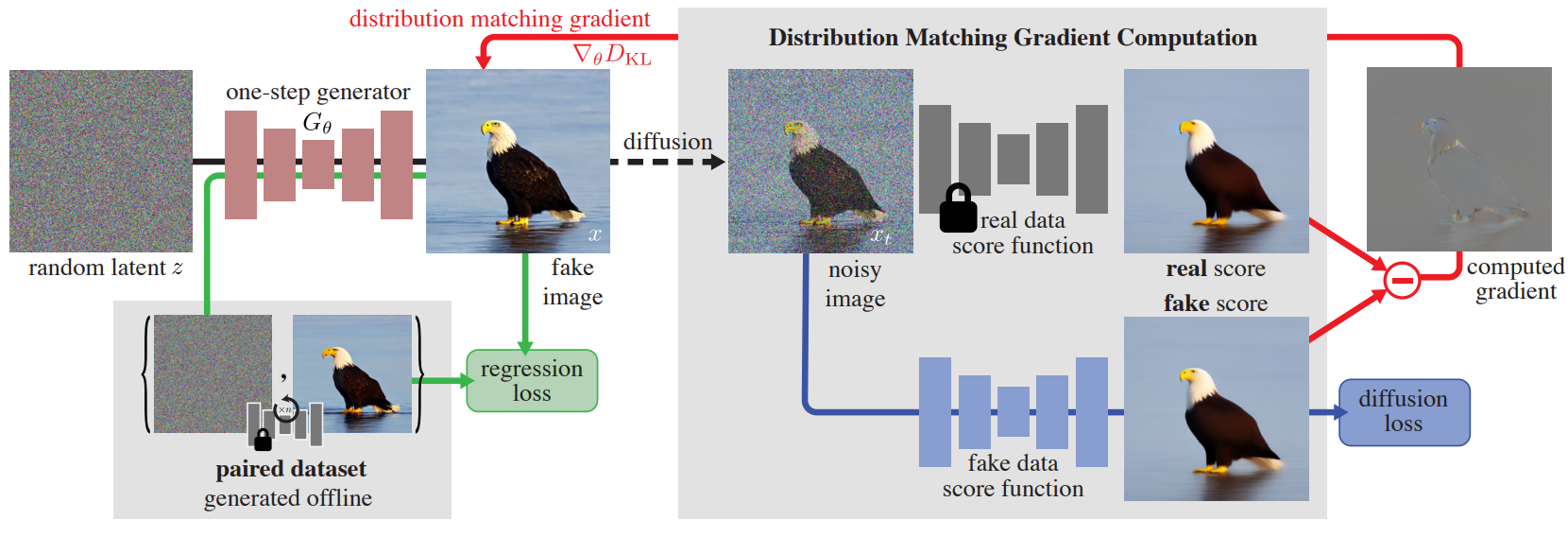
- 사전에 훈련된 diffusion model (base model: )을 one-step generator (student model: )로 증류하여 반복적인 샘플링 없이도 생성하는 것을 목표로 한다.
- 같은 분포로부터 샘플링하는 것을 원하지만, 정확히 같은 매핑을 재생산하는 것은 딱히 원하지 않는다.
- GAN과 비슷한 흐름으로, student model의 출력을 fake라 칭하고, 반대로 train distribution에 해당되는 실제 훈련 이미지를 real이라고 정의한다.
- 훈련에는 총 두 개의 손실 함수가 사용되는데 이때, 서로 다른 두 개의 score function의 차로 gradient가 표현되는 diffusion loss와, real과 fake 이미지 간의 차로 표현되는 regression loss가 있다.
- 다양한 강도의 gaussian noise로 perturbation된 이미지를 두 개의 diffusion model에 넣어서 real score과 fake score을 설계한다.
3.1 Pretrained base model and One-step generator
- 사전 훈련된 Diffusion Model인 가 있다는 가정하에 진행되며, 이때 는 기존의 DDPM 방식과 동일한 forward/backward process를 지니며, EDM과 Stable Diffusion에서 제시한 사전 훈련된 모델을 사용했다고 한다.
- One-step generator 는 base diffusion과 구조가 같고, 초기 파라미터가 같지만, time-conditioning이 없는 형태이다.
3.2 Distribution Matching Loss
- 이상적으로, 가 와 구분 불가능한 이미지를 생성하길 원하기 때문에 real image와 fake image 각각의 분포인 간의 KL divergence가 다음 식과 같이 최소가 되도록 한다:
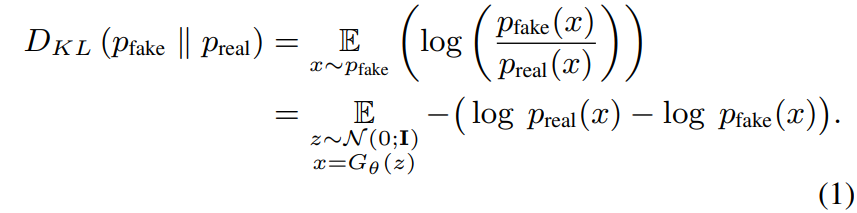
- 해당 손실 함수의 확률밀도를 추정하는 것은 불가능 하지만, 경사하강법을 통해 generator를 학습시키기 위해서 필요한 것은 에 관한 gradient이기 때문에 불가능하지 않다.
- 식 (1)의 gradient 만을 취해서 gradient 업데이트를 나타내면 다음 식과 같다:
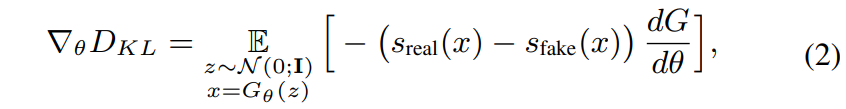
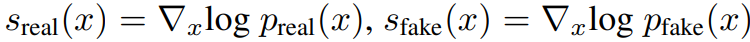
- 위의 s에 관한 식들은 각각 real과 fake의 분포를 나타내며 직관적으로 보면, 은 입력 를 의 모드들에 가깝게 움직이고, 는 그들을 멀어지도록 한다.
- 하지만 여전히, fake sample에 대해서는 분포가 소멸된다는 점과, 우리가 사용하는 score estimator은 diffused 된 분포에 대한 score만 제공한다는 두 가지 문제점이 존재한다.
- Score-SDE는 이 두 문제에 해답을 제시한다.
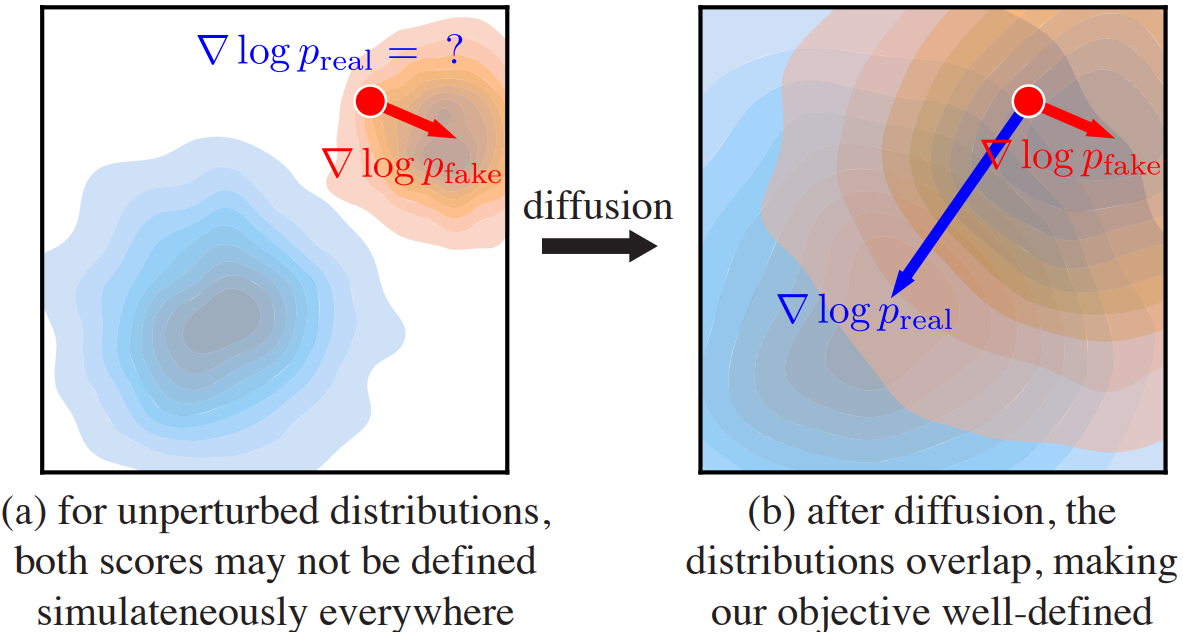
- 데이터 분포를 다양한 표준편차를 가진 랜덤 가우시안 노이즈를 통해 perturb하는 것으로 점이 아닌 주변까지 커버하는 흐려진 분포의 집합을 얻는다.
- 이로 인해 분포들끼리 겹치게 되고, 식 (2)의 gradient 계산이 잘 되도록 만든다.
- Real score는 기존의 base diffusion model 인 를 freeze한 채로 사용하여 구하게 된다. (Song et al.의 방식)
- Fake score도 같은 방식으로 구하지만, one-step generator의 생성 결과가 학습을 해나감으로써 변하기 때문에 와 같은 모델로 초기화한 모델을 식에 기반하여 가중치 업데이트를 진행하며 구한다.
- 최종적인 gradient 업데이트 식은 기존의 식(2)에 위에서 새롭게 정의한 변수들을 추가한 다음과 같은 식이 된다:
- 이때, 라는 시간종속적인 scalar 가중치를 추가하여 dynamics를 개선한다고 하며, 식은 다음과 같다:
- Regression loss는 다음 식과 같이 주어진다:
Experiments
4.1 Class-conditional Image Generation
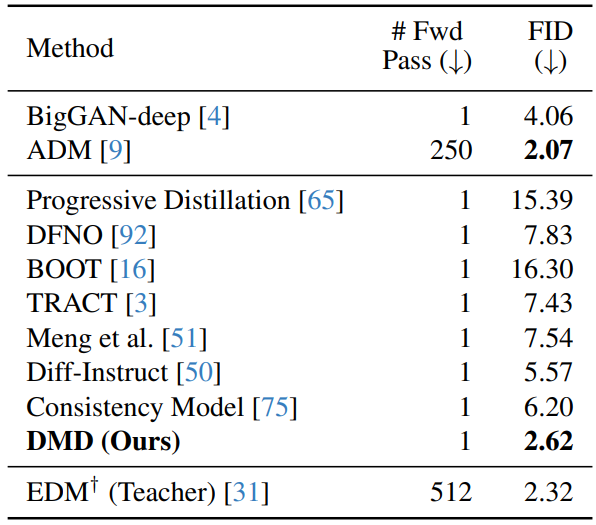
- ImageNet-64x64 데이터셋에 대해 진행한 정량적 실험 결과이다.
- 1번의 step 수로도 EDM(Teacher)모델과 비슷한 성능을 보이며, 기존의 1 step혹은 few-step 모델들과 비교했을 때 최고 성능을 보인다.
4.2 Ablation Studies

- 본 논문의 방법에서 분포 매칭 적용 시와 적용하지 않았을 시의 정성적 평가 비교이다.
- 좌측(논문의 방법)이 더욱 현실적이고 구조적 결합의 완성도가 높은 이미지를 생성하는 것을 확인할 수 있다.
- 생성 시 랜덤 시드는 동일하게 고정했다고 한다.

- 동일하게 Regression Loss를 사용했을 때와, 제거했을 때의 정성적 비교이다.
- 적용하지 않은 경우 우측과 같이 redundant한 생성을 하는 경우가 있었다고 한다.
4.3 Text-to-Image Generation
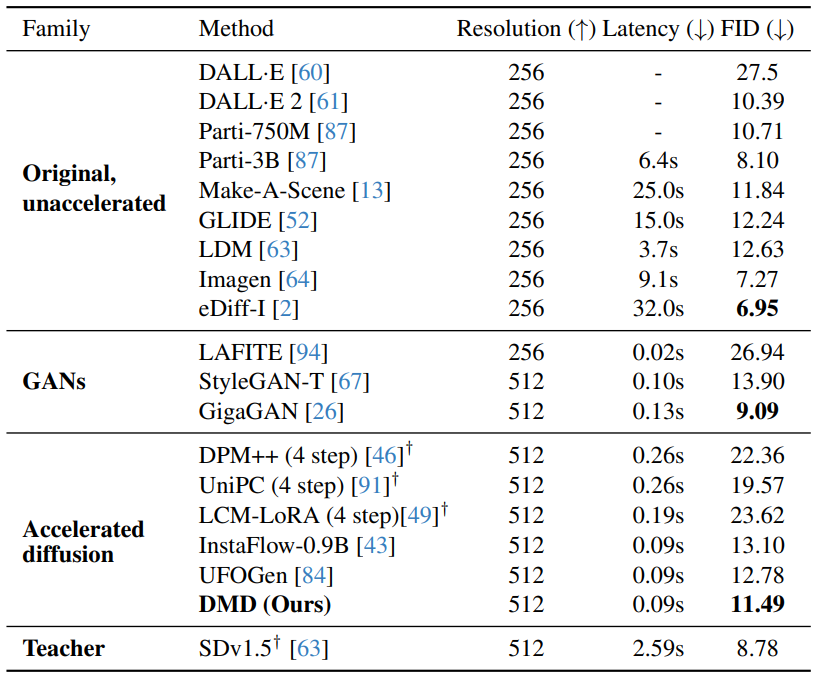
- MS COCO 데이터셋에 대해 text-to-image 생성을 진행한 정량적 실험 결과이다.
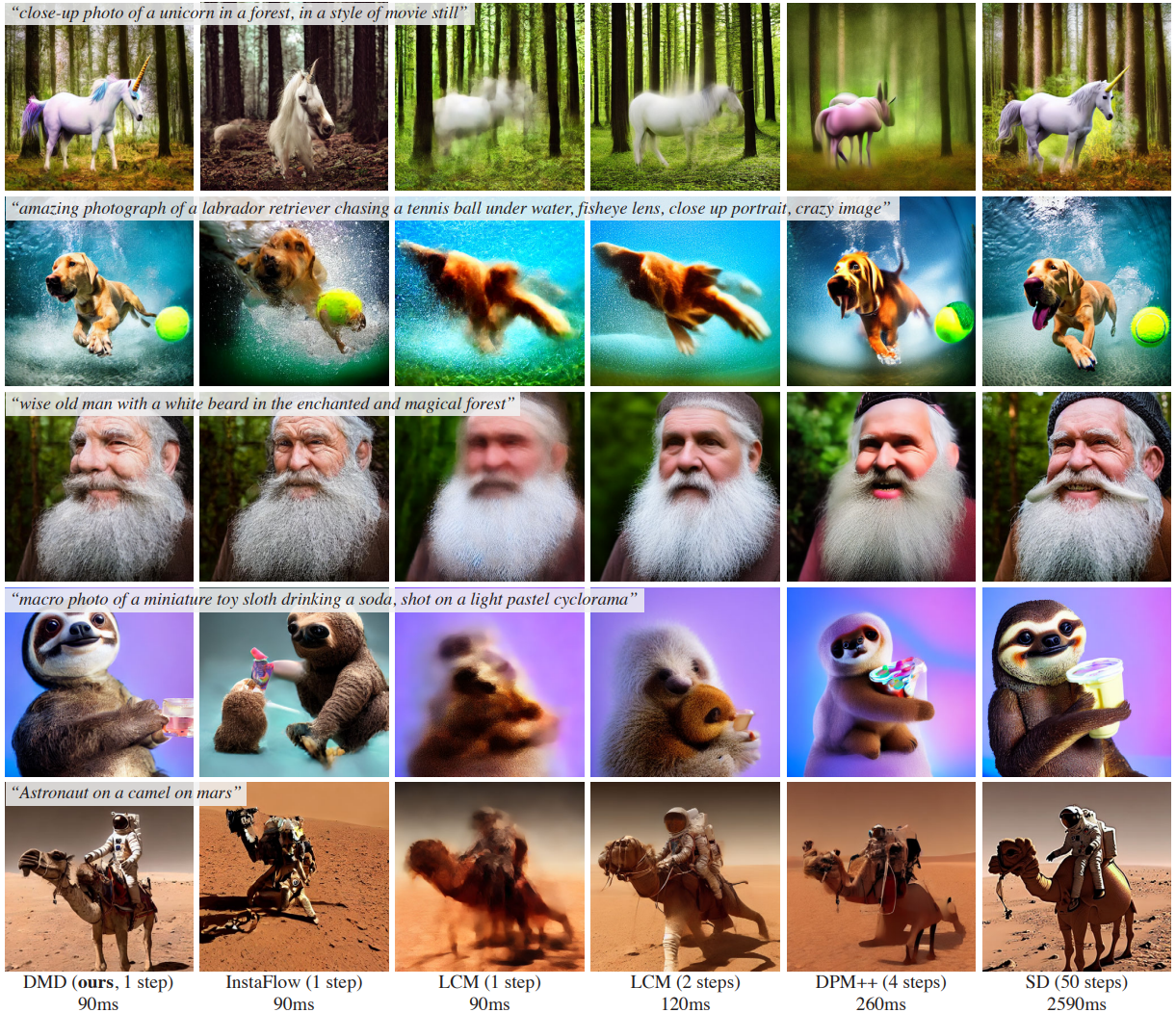
T2I Generation Qualitative Comparison
Reference
Paper URL:https://arxiv.org/pdf/2311.18828
