
📚 문제 설명
땅따먹기 게임을 하려고 합니다. 땅따먹기 게임의 땅(land)은 총 N행 4열로 이루어져 있고, 모든 칸에는 점수가 쓰여 있습니다. 1행부터 땅을 밟으며 한 행씩 내려올 때, 각 행의 4칸 중 한 칸만 밟으면서 내려와야 합니다. 단, 땅따먹기 게임에는 한 행씩 내려올 때, 같은 열을 연속해서 밟을 수 없는 특수 규칙이 있습니다.
예를 들면,
| 1 | 2 | 3 | 5 |
| 5 | 6 | 7 | 8 |
| 4 | 3 | 2 | 1 |
로 땅이 주어졌다면, 1행에서 네번째 칸 (5)를 밟았으면, 2행의 네번째 칸 (8)은 밟을 수 없습니다.
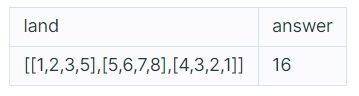
마지막 행까지 모두 내려왔을 때, 얻을 수 있는 점수의 최대값을 return하는 solution 함수를 완성해 주세요. 위 예의 경우, 1행의 네번째 칸 (5), 2행의 세번째 칸 (7), 3행의 첫번째 칸 (4) 땅을 밟아 16점이 최고점이 되므로 16을 return 하면 됩니다.
제한사항
- 행의 개수 N : 100,000 이하의 자연수
- 열의 개수는 4개이고, 땅(land)은 2차원 배열로 주어집니다.
- 점수 : 100 이하의 자연수
🔎 입출력 예
💻 코드
import java.math.*;
class Solution {
int solution(int[][] land) {
int answer = 0;
for(int i=1; i<land.length; i++) {
land[i][0] += Math.max(Math.max(land[i-1][1],land[i-1][2]),land[i-1][3]);
land[i][1] += Math.max(Math.max(land[i-1][0],land[i-1][2]),land[i-1][3]);
land[i][2] += Math.max(Math.max(land[i-1][0],land[i-1][1]),land[i-1][3]);
land[i][3] += Math.max(Math.max(land[i-1][0],land[i-1][1]),land[i-1][2]);
}
for(int i=0; i<4; i++) {
answer = Math.max(answer,land[land.length-1][i]);
}
return answer;
}
}💻 다른 코드
import java.math.*;
class Solution {
int solution(int[][] land) {
int[][] dp = new int[land.length][4];
for (int i = 0; i < 4; i++) {
dp[0][i] = land[0][i];
}
for (int i = 1; i < land.length; i++) {
for (int j = 0; j < land[i].length; j++) {
for (int k = 0; k < land[i].length; k++) {
if (j != k) {
dp[i][j] = Math.max(dp[i][j], dp[i - 1][k] + land[i][j]);
}
}
}
}
int max = 0;
for (int i = 0; i < 4; i++) {
max = Math.max(max, dp[land.length - 1][i]);
}
return max;
}
}📖 Solution
이 문제는 DP를 사용해서 풀어야하는 문제이다.
나는 DP 문제를 접해본적이 없어 먼저 개념을 이해한 후 참고하여 풀어보기로 하였다.
i 번째 행에서 열이 선택되었을때 i-1번째 행 중 선택된 열을 제외한 나머지들 중 최대값을 구해서 더하는 방식으로 풀면된다!
Dynamic Programming (동적계획법)
주어진 문제를 풀기위해 문제를 여러개의 하위 문제로 나누어 푸는 방법을 말한다!
✔ 메모이제이션 기법으로 속도 향상
- 답을 여러번 계산하는 대신 한번만 계산하고 계산한 값을 재사용함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 해준다
그럼 Dynamic Programming의 조건은 뭘까 ❓
- 중복되는 작은 문제들 -> 메모이제이션 기법 사용
- 최적 부분 구조 -> 전체 문제의 최적해가 부분 문제의 최적해들로써 구성
탑다운 ⬇(Top-down), 바텀업 ⬆(Bottom-up)
🔎 탑다운 (재귀 호출 사용)
: 큰 문제를 해결하기 위해 작은 문제를 호출하는 방식
탑다운 방식의 장점은 가독성이 좋고, 본래 점화식을 이해하기 쉽다.
import java.util.Scanner;
public class FibonacciNumber_TopDown {
// Memoization을 적용할 배열.
static long[] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
dp = new long[n + 1];
// n번째 피보나치 수를 구하고 출력하라.
System.out.println(Fibonacci(n));
sc.close();
}
private static long Fibonacci(int n) {
// 기저 조건(피보나치 수열의 초항).
if (n == 1 || n == 2) {
return dp[n] = 1;
}
// 만일, 저장된 값이 존재하는 경우 기억된 값을 바로 넘겨준다.
if (dp[n] != 0) {
return dp[n];
}
// 그렇지 않은 경우, 기저 조건까지 내려가서 구해진 값을 저장하면서 재귀를 전이한다.
else {
return dp[n] = Fibonacci(n - 1) + Fibonacci(n - 2);
}
}
}🔎 바텀업 (반복문 사용)
: 가장 작은 문제들부터 답을 구해가며 전체 문제의 답을 찾는 방식
- DP의 전형적인 형태!
함수를 별개로 부르지 않아 시간과 메모리를 소량 더 절약할 수 있다는 점이 있다.
import java.util.Scanner;
public class FibonacciNumber_BottomUp {
// Tabulation을 적용할 배열.
static long[] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
dp = new long[n + 1];
// 기저 조건을 바탕으로 초항을 먼저 초기화 해둔다.
dp[1] = 1;
dp[2] = 1;
// n번째 피보나치 수를 구하고 출력하라.
System.out.println(Fibonacci(n));
sc.close();
}
private static long Fibonacci(int n) {
// 기저 조건을 기반으로 테이블을 채워나간다(Tabulation).
for(int i = 3; i <= n; i++) {
// 점화식을 이용하여 쉽게 구할 수 있다.
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
}