BFS와 DFS는 그래프를 탐색할 때 사용하는 알고리즘입니다. 이 포스팅에서 소개할 내용은 다음과 같습니다.
0. 그래프에 대하여.
1. BFS가 무엇인가.
2. 소스코드로 이해하는 BFS.
3. DFS가 무엇인가.
4. 소스코드로 이해하는 DFS.
5. 풀어보면 좋은 응용 문제.
0. 그래프에 대하여.
위에서 간단하게 BFS와 DFS는 '그래프'를 탐색할 때 사용한다는 것을 언급했습니다. 그러면 BFS와 DFS라는 알고리즘을 배우기 전에, 코딩에서 말하는 '그래프'가 무엇인지부터 알아보겠습니다.
그래프는 정점(Vertex)과 간선(Edge)으로 이루어져 정점 간의 관계를 표현하는 조직도입니다. 그래프의 형태는 무수히 많은데, 그 중 간단한 그래프를 소개하겠습니다.
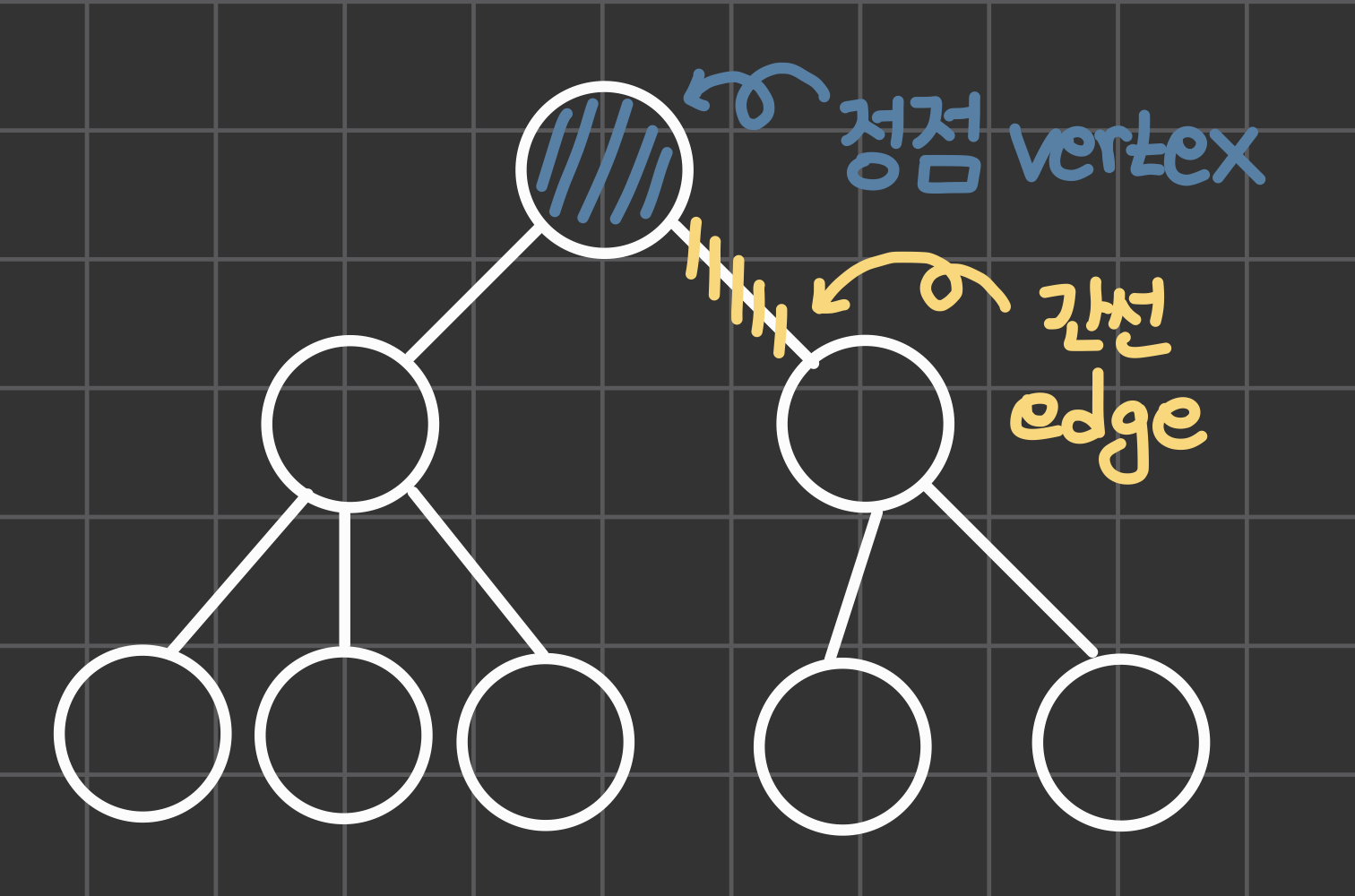
1. BFS가 무엇인가.
BFS는 Breadth First Search의 약자로, '너비 우선 탐색'이란 뜻입니다.
'너비'라는 단어에서 알 수 있듯이, BFS는 그래프가 있을 때 너비가 점점 퍼져가는 형태로 그래프를 탐색합니다.
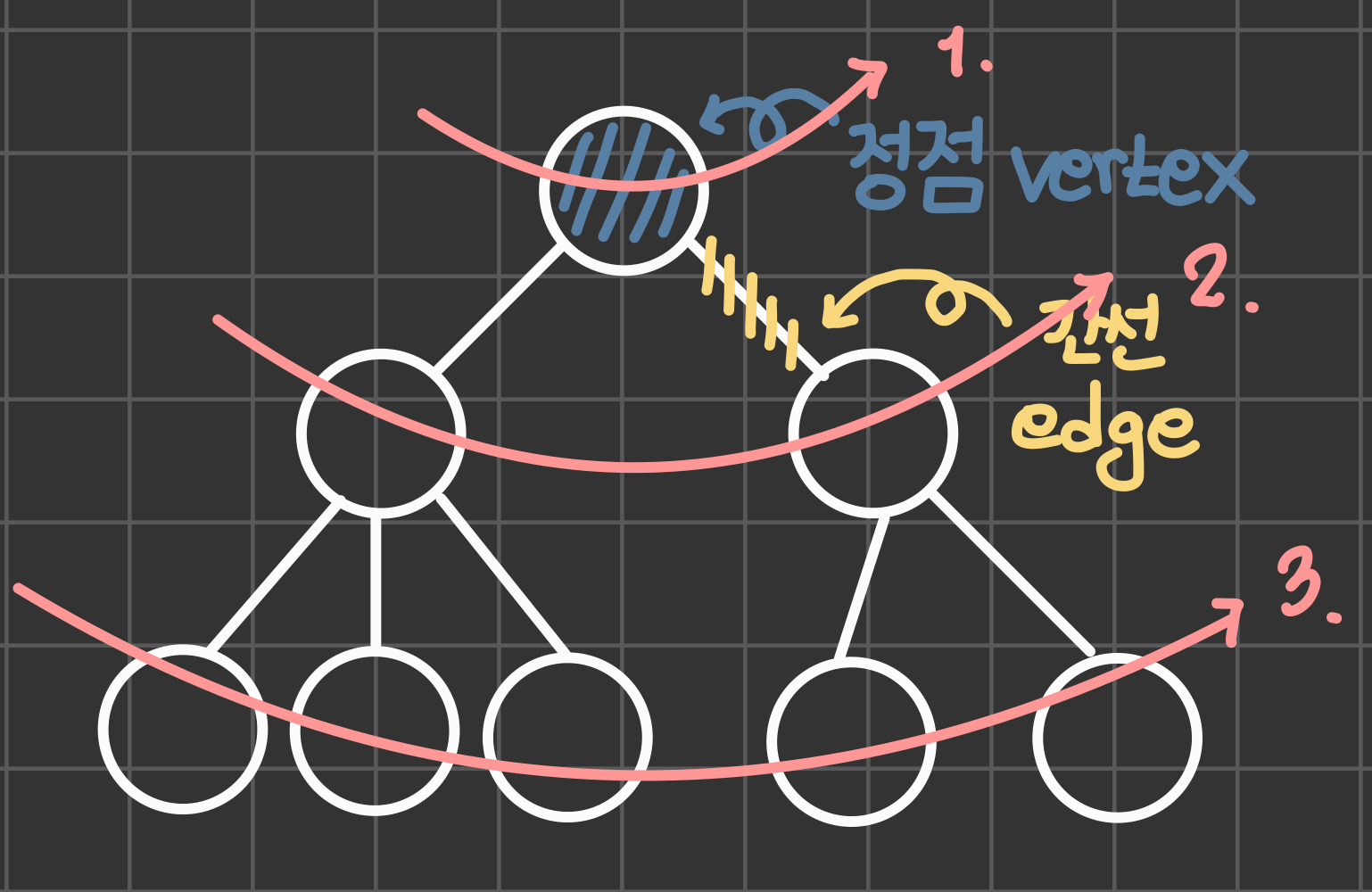간단한 예를 통해 살펴보자면,
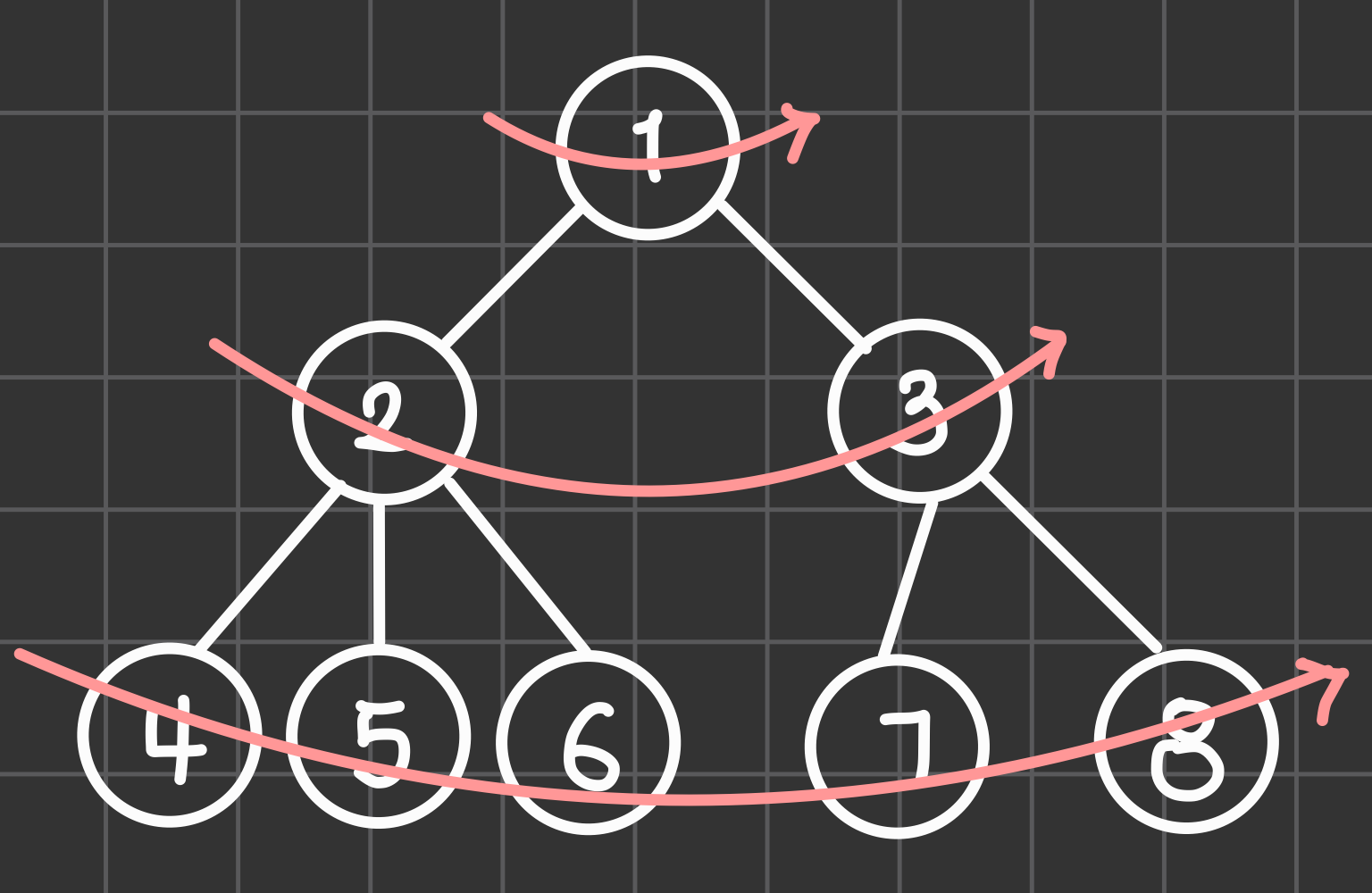위 그래프에서 BFS 알고리즘을 사용하게 되면, 1-2-3-4-5-6-7-8 의 순서대로 그래프를 탐색하게 됩니다. 개념을 응용하기 위해, 소스코드를 통해 BFS를 살펴보겠습니다.
2. 소스코드로 이해하는 BFS.
백준 BOJ_1260(BFS와 DFS)을 통해 알아보겠습니다. 먼저, 전체적인 코드는 아래와 같습니다.
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> vec[1003];
queue<int> q;
bool check[1003];
void BFS(int);
int main() {
int N, M, V;
scanf("%d %d %d", &N, &M, &V);
int a, b;
for (int i=0; i < M; i++) {
scanf("%d %d", &a, &b);
vec[a].push_back(b);
vec[b].push_back(a);
}
for (int i = 1; i <= N; i++)
sort(vec[i].begin(), vec[i].end());
BFS(V);
printf("\n");
return 0;
}
void BFS(int start) {
q.push(start);
check[start] = true;
printf("%d ", start);
while (!q.empty()) {
for(int i = 0; i < vec[start].size(); i++) {
if (check[vec[start][i]] == false) {
q.push(vec[start][i]);
check[vec[start][i]] = true;
}
}
q.pop();
check[q.front()] = true;
if (!q.empty())
printf("%d ", q.front());
start = q.front();
}
return;
}3. DFS가 무엇인가.
DFS는 Depth First Search의 약자로, '깊이 우선 탐색'이란 뜻입니다.
BFS는 퍼져나가는 형태로 그래프를 탐색한다고 했을 텐데요. 이와 달리, DFS는 '깊이'라는 단어에서 알 수 있듯이, 한 곳만 파고드는 형태로 그래프를 탐색합니다.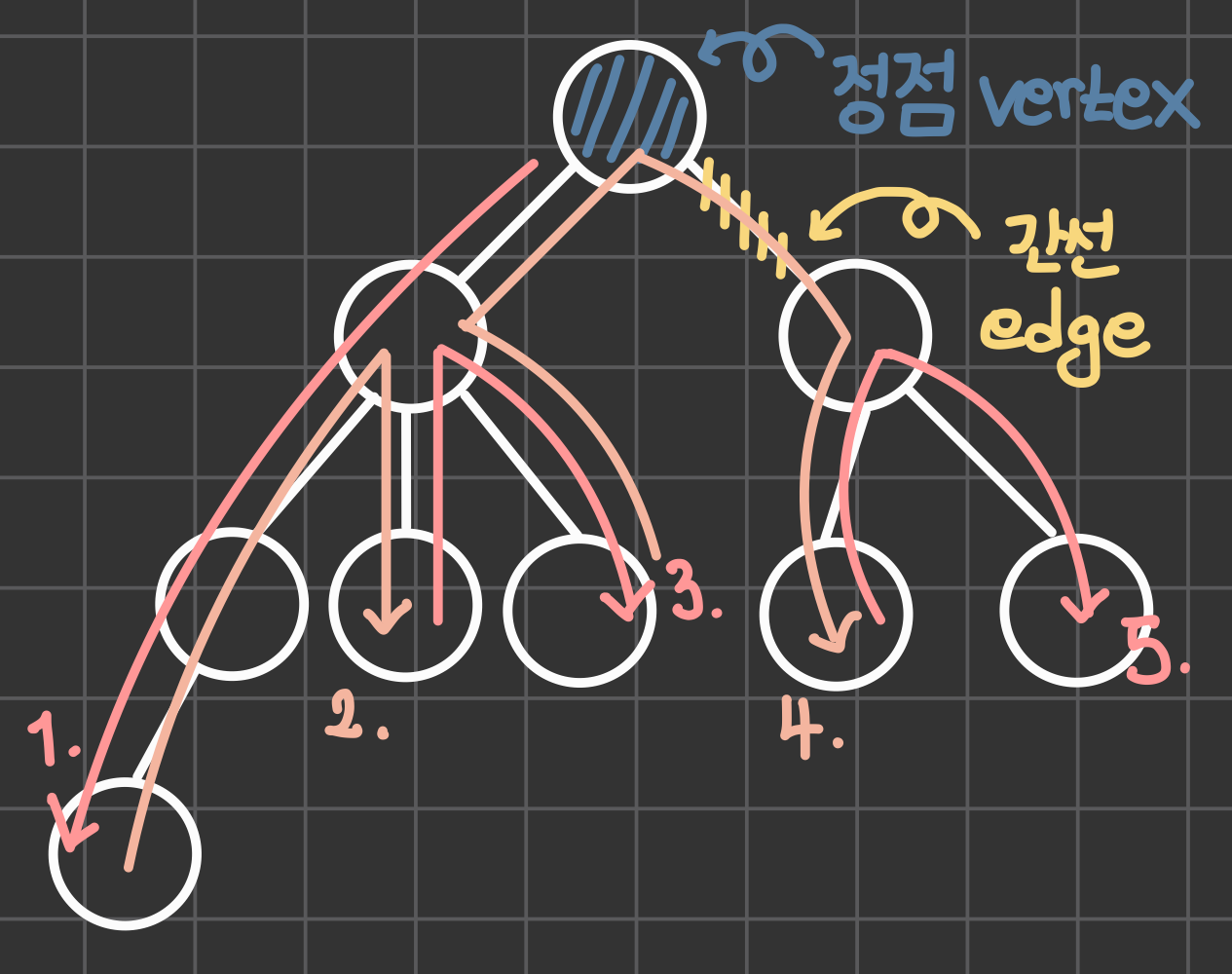
간단한 예를 통해 살펴보자면,
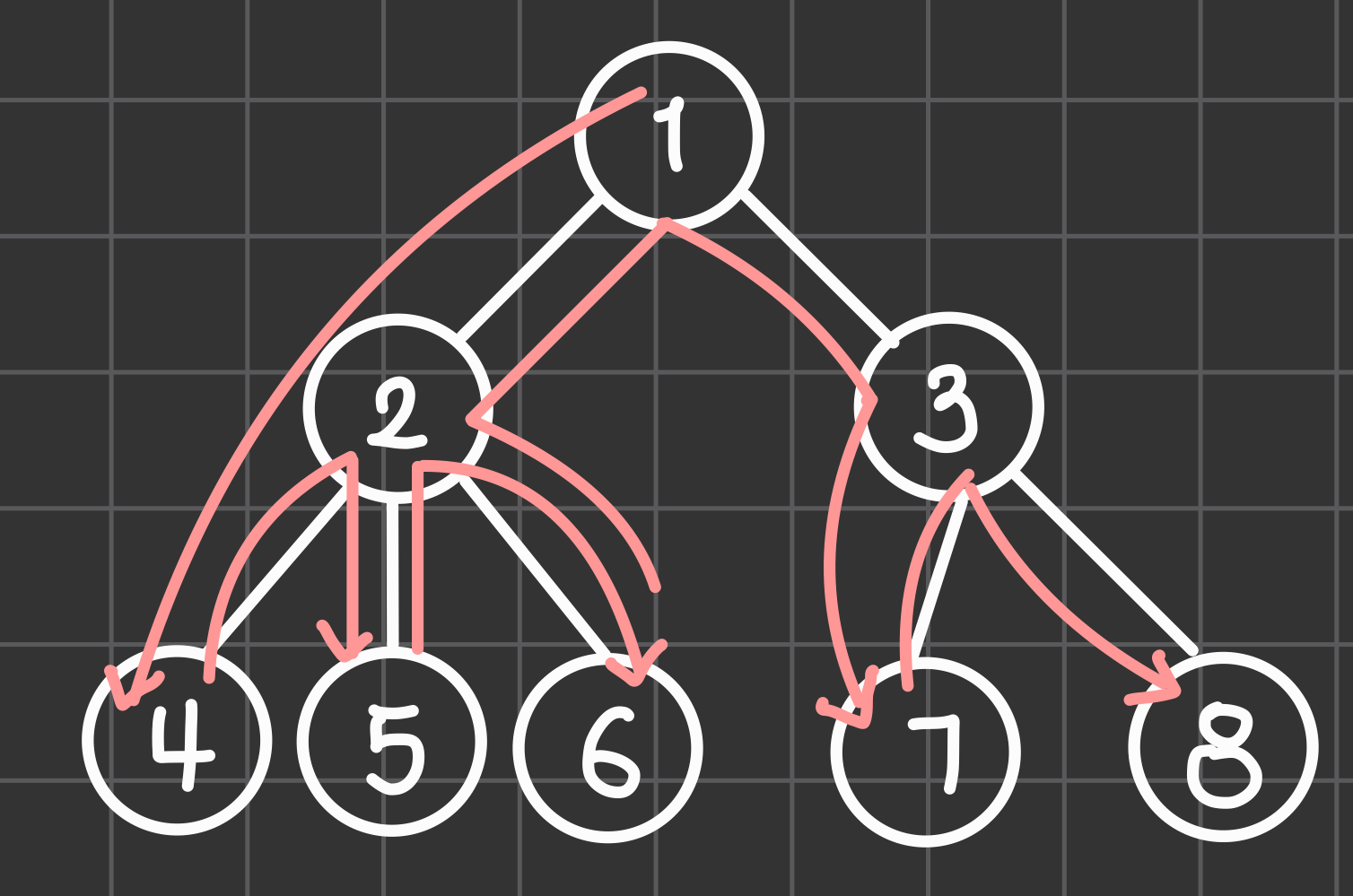위 그래프에서 DFS 알고리즘을 사용하게 되면, 1-2-5-6-3-7-8 의 순서대로 그래프를 탐색하게 됩니다. 마찬가지로, DFS도 개념을 응용하기 위해, 소스코드를 통해 살펴보겠습니다.
4. 소스코드로 이해하는 DFS.
백준 BOJ_1260(BFS와 DFS)을 통해 알아보겠습니다. 먼저, 전체적인 코드는 아래와 같습니다.
#include <cstdio>
#include <queue>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> vec[1003];
queue<int> q;
bool check[1003];
void DFS(int);
int main() {
int N, M, V;
scanf("%d %d %d", &N, &M, &V);
int a, b;
for (int i=0; i < M; i++) {
scanf("%d %d", &a, &b);
vec[a].push_back(b);
vec[b].push_back(a);
}
for (int i = 1; i <= N; i++)
sort(vec[i].begin(), vec[i].end());
DFS(V);
printf("\n");
return 0;
}
void DFS(int start) {
printf("%d ", start);
check[start] = true;
for (int i = 0; i < vec[start].size(); i++) {
int K = vec[start][i];
if (check[K] != true) {
DFS(K);
}
}
return;
}5. 풀어보면 좋은 응용 문제.
