1. AVL 트리

AVL 트리란?

Adelson-Velskii와 Landis에 제안된 트리
각 노드에서 왼쪽 서브트리와 오른쪽 서브트리의 높이 차이가 1 이하인 이진 탐색 트리

AVL 트리의 특징은?

1. 균형 트리
2. 탐색 시간: O(log n)
3. 삽입 시간: O(log n)
4. 삭제 시간: O(log n)

2. 균형 인수

균형인수란? (balance factor)

균형 인수 = 왼쪽 서브 트리의 높이 - 오른쪽 서브 트리의 높이
모든 노드의 균형인수가 +- 1이하이면 AVL 트리임

3. 탐색 연산

탐색 연산의 시간복잡도는?

O(log n)
AVL 트리도 이진 탐색 트리이므로, 일반적인 이진 탐색 트리의 탐색 시간복잡도와 동일

4. 삽입 연산

삽입 연산의 시간복잡도는?

O(log n)

삽입 연산으로 균형이 깨지면?

삽입 연산시, 삽입되는 위치에서 루트까지의 경로에 있는 조상 노드들의 균형 인수에 영향을 줄 수 있음
새로운 노드부터 균형인수가 +-2가 된 가장 가까운 조상 노드까지를 회전하여 균형을 다시 잡아야 한다.

삽입시 균형이 깨지는 4가지 경우

1. LL (left-left)

• 균형 깨짐
  

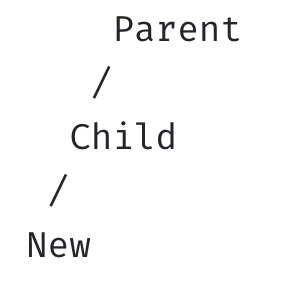
• 균형 회복: Child 기준으로 오른쪽으로 회전
  

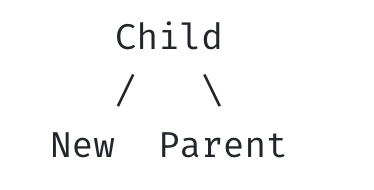
2. LR (left-right)

• 균형 깨짐
  

• 균형 회복: New 기준으로 왼쪽으로 회전 + Child 기준으로 오른쪽 회전
  

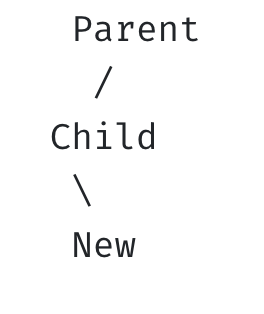
3. RR (right-right)

• 균형 깨짐
  
• 균형 회복: Child 기준으로 왼쪽으로 회전
  

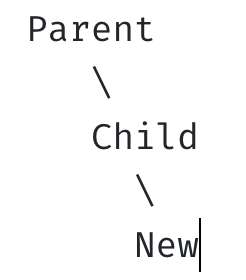
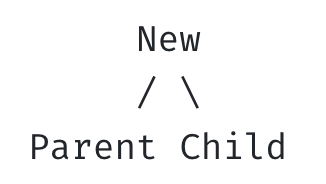
4. RL (right-left)

• 균형 깨짐
  
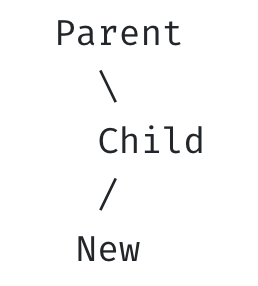
• 균형 회복: New 기준으로 오른쪽으로 회전 + Child 기준으로 왼쪽으로 회전
  

5. 코드

typedef struct AVLNode {
	int key;
    AVLNode* left;
    AVLNode* right;
}

AVLNode* rotate_right(AVLNode* parent) {
	AVLNode* child = parent -> left;
    parent -> left = child -> right;
    child -> right = parent;
    return child; // 새로운 루트 반환
}

AVLNode *rotate_left(AVLNode* parent) {
	AVLNode* child = parent -> right;
    parent -> right = child -> left;
    child -> left = parent;
    return child;
}

int get_height(AVLNode *node) {
	int height = 0;
    if(node != NULL) {
    	height = 1 + max(get_height(node -> left), get_height(node -> right);
    }
    return height;
}

int get_balance(AVLNode *node) {
	it (node == NULL) return 0;
    return get_height(node->left) - get_height(node->right);
}


AVLNode* insert(AVLNode node, int key) {
	if (node == NULL) return create_node(key);
    
    if (key < node -> key) {
    	node -> left  = insert(node->left, key);
    else if (key > node -> key) {
    	node -> right = insert(node-> right, key);
    else
    	return node;
    
    int balance = get_balance(node);
    
    // LL
    if (balance > 1 && key < node -> left -> key) {
    	return rotate_right(node);
    }
    
    // LR
    if (balance > 1 && key > node -> left -> key) {
    	node -> left = rotate_left(node->left);
        return rotate_right(node);
    }
    
    // RR
    if (balance < -1 && key > node -> right -> key) {
    	return rotate_left(node);
    }
    
    // RL
    if (balance < -1 && key < node -> right -> key {
    	node -> right = rotate_right(node->right);
        return rotate_left(node);
    }
    
    return node;
 }