1. 이진 최소 힙

이진 최소 힙이란?

• 완전 이진 트리 기반의 자료구조
• 노드의 값은 자식 노드 값보다 작거나 같음
  -> 루트 노드에 가장 작은 수가 위치함
• 배열을 이용해 구현하는 경우가 많음
  -> 기준 인덱스가 i라면, 부모인덱스: i/2, 왼쪽 자식 인덱스: 2i, 오른쪽 자식 인덱스: 2i+1

2. 완전 이진 트리

이진 트리란?

각 노드가 최대 2개의 자식 노드를 가질 수 있는 트리

완전 이진 트리

• 마지막 레벨을 제외한 모든 레벨은 노드가 가득 채워 있어야 함

• 마지막 레벨에서는 왼쪽부터 차례대로 노드가 채워 있어야 함

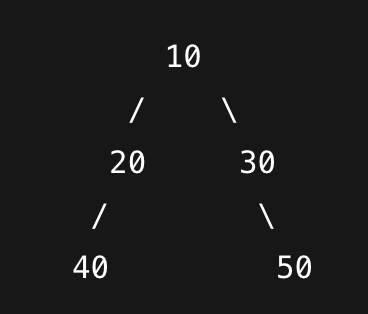
  • 완전 이진트리 ✅
    
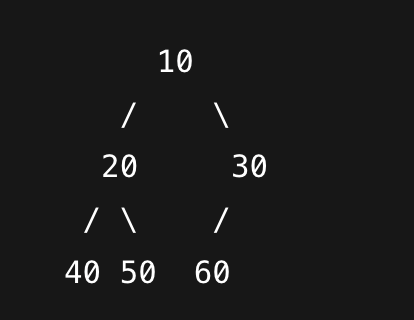
  • 완전 이진트리 ❌
    
    • 20의 오른쪽 자식이 비워져 있는데 30의 오른쪽 자식이 채워져 있음

힙에서 완전 이진 트리를 사용하는 이유는?

• 완전 이진 트리를 사용하면 배열만으로 힙을 표현할 수 있음
  • 완전 이진 트리는 인덱스 규칙이 간단하므로 배열로도 구현 가능함
• 삽입과 삭제 연산이 간단
  • 힙 삽입: 항상 배열의 마지막 위치에 삽입
    • 완전 이진트리는 왼쪽노드부터 차례로 채워져야 하므로 삽입되는 위치가 고정됨
  • 힙 삭제: 루트 제거 후 마지막 원소를 루트로 올림
    • 빈자리가 생기지 않고 다시 완전 이진 트리 유지 가능
• 트리 높이가 최소화됨
  • 완전 이진 트리는 항상 왼쪽 노드부터 빈틈없이 채워지므로 높이가 최소화되고 연산의 성능이 올라감
  • 연산 시간 보장: O(log n)
• 균형 유지

3. 삽입 연산

삽입 연산 순서

1. 새로운 노드를 배열의 마지막(트리의 마지막 위치)에 삽입
2. 부모의 비교하여, 부모보다 작으면 부모와 위치 교환
3. 2번 과정을 루트에 도달하거나 부모모다 크거나 같아질 때까지 반복

삽입 연산 시간 복잡도

• 최선: O(1) <- 부모보다 크거나 같은 경우
• 평균: O(log n)

4. 삭제 연산

삭제 연산 순서

1. 루트(최솟값) 제거
2. 마지막 원소를 루트로 이동
3. 새로운 루트의 값이 자식보다 크면, 자식 노드 중 더 작은 자식 노드와 교환
4. 자식 노드들보다 더 작은 값이 되는 때까지 3번 과정을 반복

삭제 연산 시간 복잡도

• 최선: O(1)
• 최악: O(log n)
• 평균: O(log n)