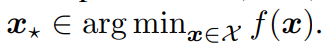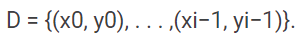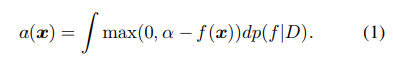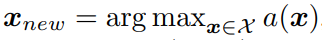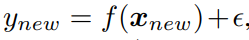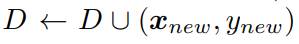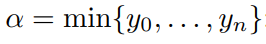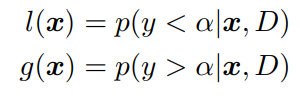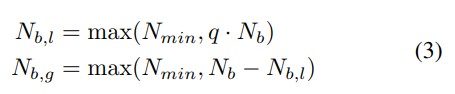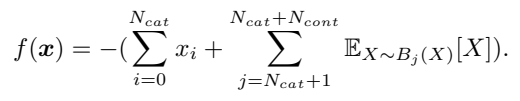논문 번역

저자

• Stefan Falkner, Aaron Klein, Frank Hutter,
• Department of Computer Science, University of Freiburg,
  Freiburg, Germany. Correspondence to: Stefan Falkner
  sfalkner@informatik.uni-freiburg.de.

Abstract

최신의 딥러닝 메소드들은 많은 하이퍼파라미터에 매우 예민하고, 굉장히 긴 학습시간을 가지기 때문에 vanilla Bayesian하이퍼 파라미터 최적화는 일반적으로도 계산상으로도 불가능 합니다.

또한, random search기반 bandit-based configuration evaluation(설정평가)는 guidance(지침)이 부족하고, 빠르게 최적의 파라미터를 얻을 수 없습니다.

여기서 이 논문은 Bayesian최적화의 장점과 bandit-based의 장점인 strong anytime performance(어느 경우에서나 강력한 성능) 와 fast convergence to optimal configurations(최적의 구성으로 빠른 수렴)을 합친 메소드를 제안합니다.

이 메소드는 highdimensional toy function, support vector machines, feed-forward neural networks, Bayesian neural networks, deep reinforcement learning 그리고 convolutional neural networks을 포함하는 다양한 문제에서 새롭고 실용적인 최신 하이퍼파라미터 최적화를 진행할 수 있습니다.

1. Introduction

머신러닝은 최근 광범위한 분야에서 많은 성공을 이뤘지만, 수많은 내부 하이퍼파라미터의 올바른 세팅에 어느때보다 크게 의존하고 있습니다.

또, 딥러닝의 최신 application을 위한 모델은 점점더 커지며, 이에따라 계산비용이 폭발적으로 증가하고 있습니다. 그러면서도 연구자와 실무자들은 자동으로 하이퍼파라미터를 설정하기를 원합니다.

특히, 아래 제약조건들은 hyperparameter optimization(HPO)문제에 대한 요구사항들을 만족할 실질적인 해답을 요구합니다.

1. Strong Anytime Performance (언제 어디서나 강력한 성능)

지금의 대규모 신경망은 보통 몇 일에서 몇 주간의 훈련시간이 소요되기 때문에, 블랙박스 방법으로 최적화하는 HPO메소드는 엄청난 리소스를 요구합니다.

대부분의 연구자와 실무자가 개발 중에 감당할 수 있는 예산은 작은 모델조차도 완전히 훈련허자 못할만큼 여유롭지 않을 때가 있습니다. 그렇기때문에, HPO 메소드는 반드시 작은 예산으로도 블랙박스 방법 이상의 성능을 보여야 합니다.

2. Strong Final Performance (강력한 최종 성능)

반면에 모델을 배포할 때 가장 중요한 것은, HPO메소드가 충분한 비용을 들여 찾아낸 최종 하이퍼파라미터 구성의 최종 성능입니다.

무수히 많은 하이퍼파라미터 조합에서 최고의 성능을 낼 수 있는 하이퍼파라미터 구성을 찾기위해서는 어떠한 가이드가 필요하기 때문에, random search기반 방법은 강력한 최종 성능을 내기 어렵습니다.

3. Effective Use of Parallel Resources (병렬 리소스의 효과적 사용)

병렬 컴퓨팅의 부상으로 대규모 병렬 컴퓨팅리소스를 사용하는 곳이 많아졌다(예: 클러스터, 클라우드 컴퓨팅). 실용적인 HPO메소드는 이러한 리소스를 최대한 효과적으로 사용할 수 있어야 합니다.

4. Scalability (확장성)

현대의 심층신경망은 많은 하이퍼파라미터들의 세팅들을 요구합니다. 예를 들어, Architectural choices(the number and width of layers), 최적화 하이퍼파라미터(learning rate schedule, momentum, batch size etc...), 정규화 하이퍼파라미터(weight decay, dropout rates) 들의 설정이 필요합니다.

따라서, 실용적 HPO메소드는 몇개에서 수십개에 이르는 하이퍼파라미터들을 쉽게 처리할 수 있어야 합니다.

5. Robustness & Flexibility (견고성 및 유연성)

하이퍼파라미터의 최적화문제는 머신러닝의 하위분야에 따라 매우 다양합니다. 예를들어, 심층강화학습 시스템은 매우 noisy하다고 알려진 반면, 확률론적 심층 학습은 몇개의 주요 하이퍼 파라미터에 매우 민감하게 반응합니다.
또, 하이퍼파라미터가 각각 다른유형(예: binary, categorical, integer, continuous)일 때, 유연하고 효과적으로 처리할 수 있어야 합니다.

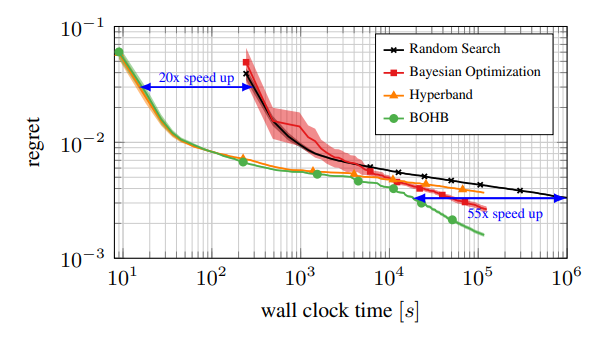
• 그림1. 6개의 하이퍼파라미터 최적화의 일반적인 결과에 대한 그림입니다. 4가지 방법으로 찾은 최적의 설정에 대한 regret을 시간을 기준으로 보여주고 있습니다. Hyperband 방법은 모든 때에 강력한 성능을 가지고 있으나, 계산량이 많아질 수록 제 성능을 발휘하지 못하고 Random search에 밀리게 된다. 반대로 Bayesian 최적화는 느리게 시작하지만(random search처럼) 시간만 충분하다면 Hyperband보다 성능이 뛰어납니다. 본 논문에서 제안하는 BOHB 방법은 계산량이 많을 때나, 적을 때 모두에서 최고의 성능을 발취하는 것을 볼 수 있습니다.

지금까지 기존의 모든 방법들은 강점과 약점이 존재합니다. 그러나 그 중 아무것도 이러한 요구사항들을 모두 만족시키는 방법은 없다. 이 논문의 주요 기여는 여러 최적화 방법들의 장점(특히, Hyperband와 강력하고 효과적인 Bayesian 최적화기법)을 합쳐, 위 5가지 요구사항을 모두 충족하는 실용적인 HPO방법을 제안합니다. 먼저, Bayesian 최적화와 Hyperband에 대해 자세히 설명하고, 새로운 방법인 BOHB에서 이들을 결합하는 방법과, 얼마나 효과적으로 결과 시스템을 병렬화하는지 보여줍니다. 본 논문의 광법위한 실증적 평가에서는 Bayesian방법과 Hyperband방법의 가장 좋은 측면을 결합한다는 것을 보여줍니다. 이 방법은 자주 Bayesian 최적화 보다 더 빠르게 좋은 결과를 찾고, Hyperband보다 훨씬 빠르게 최고의 최적화 설정으로 수렴합니다.

2. Related Work on Model-based Hyperparameter Optimization

Bayesian 최적화기법

Bayesian 최적화는 기존의 많은 연구들에서 성공적으로 적용되었습니다. Snoek et al.(2012) 컨벌루션 신경망의 하이퍼파라미터를 최적화하여 CIFAR-10에서 최고의 성능을 보였습니다. Bergstra et al. (2014) TPE (Bergstra et at., 2011)을 사용하여 고도로 매개변수화된 3개의 컨볼루션신경망 레이어를 최적화 했습니다. Mendoza et al.(2016) 2016 AutoML 챌린지에서 자동으로 완전히 연결된 신경망에서 적합한 아키텍처와 하이퍼파라미터를 찾아 3개의 데이터셋에서 우승 했습니다.

(Shahriari et al., 2016) Aussian 프로세스는 매끄럽고, 불확실성을 잘 보정해주기 때문에, Bayesian최적화에서 가장 흔하게 쓰이는 확률적 모델입니다. 그러나 Gaussian 프로세스는 높은 차원에서는 일반적으로 잘 확장되지 않으며, 데이터포인트의 수에서 입방체 복잡성을 나타냅니다.(scalability). 또, 특별한 kernel없이는 복잡한 설정 공간에 적용되지 않으며(flexibility), 신중하게 설정된 하이퍼 우선순위가 필요합니다.(robustness).

기계학습 알고리즘의 하이퍼파라미터 최적화 속도를 높이기 위해, Bayesian 최적화는 객체 함수의 의존도를 낮춰 기존의 블랙박스 세팅을 확장하려고 합니다 (Swersky et al., 2014; Klein et al., 2017a; Swersky et al., 2013; Kandasamy et al., 2017; Klein et al., 2017c; Poloczek et al., 2017). 예를 들어, 다중 작업 Bayesian 최적화 기법(Swersky et al., 2013)은 warm-start 최적화 프로시져를 위해 작업들간의 상관관계를 활용합니다. 이 외에도 다양한 방법이 우수한 성능과 최종 성능을 달성했지만, 위에서 언급한 Gausian 프로세스를 기반으로합니다.

Hyperband

Hyperband(Li et al., 2017)는 랜덤으로 설정을 구성하고 동적 리소스를 할당하여 성공적인 부분만 사용하는 bandit 전략을 사용합니다. 다중 충실도를 사용하지 않는 Bayesian방법보다 더 높은 차원 공간에 대한 유연성과 확장성을 가지고, 항상 강력한 성능을 보여주었습니다. 그러나, 무작위로 설정을 구성하지만, 그전의 설정에서 학습하지는 않습니다. 즉, 학습을 기반으로 하는 모델 기반 방식보다 최종 성능이 저하될 수 있습니다.

3. Bayesian Optimization and Hyperband

머신러닝 알고리즘의 성능을 검증하는 모델은 x ∈ X일 때, 라고 할 수 있습니다. 하이퍼파라미터 최적화(HPO)문제는 x를 찾는 것으로 정의할 수 있습니다.

대부분의 머신러닝 알고리즘의 본질적인 무작위성으로 인해, 우리는 f(x)를 Noisy(잡음있는)결과만 관찰된다고 가정합니다. 이제, 최적화 문제를 해결하기 위한 두가지 방법인 Bayesian 최적화와 Hyperband방법을 자세히 살펴보겠습니다.

3.1. Bayesian Optimization

각 반복 i에서, Bayesian optimization (BO)는 확률모델 p(f|D)를 사용하여 이미 관측된 포인트D를 기본으로한 목적함수 f를 모델링 합니다.
BO는 탐색과 개발을 절충하는 현재모델 p(f|D)를 기반으로 획득함수 a를 사용합니다.

모델과 획득함수를 기반으로 다음 세 가지를 반복합니다.

• 1. 획득함수 a(x)를 최대화하는 새로운 x를 찾는다.
     
• 2. 목적함수 새로운y를 평가한다.
     
• 3. 데이터 새로운x와 y를 더한D를 증강하여 모델틀 다시 훈련시킵니다.
     
     일반적인 획득함수는 현재 가장 잘 관측된 값 α를 넘어서는 기대 개선(EI)입니다.
     

Tree Parzen Estimator

Tree Parzen Estimator(TPE) (Bergstra et al., 2011)는 목적함수 f를 p(f|D)로 직접 모델링 하는 대신, 커널 밀도 측정을 사용하여 밀도를 측정하는 Bayesian 최적화 기법입니다.
평가할 새로운x를 선택하기 위해 l(x)/g(x)를 최대화 합니다. 이는 Bergstra et al.(2011)에서 방정식 (1)의 EI를 최대화 하는 것과 동일함을 보였습니다. 커널 밀도 추정기의 특성으로 인해, TPE는 혼합된 연속공간과 discrete(불연속, 디지털) 공간을 쉽게 지원하고, 모델 구성의 스케일이 데이터 수에 따라 선형으로 확장됩니다.(Cubic-time을 가졌던 Gaussian processes(GPs, 가우시안 프로세스)와는 대조적이다.)

3.2 Hyperband

알고리즘 1

SuccessiveHalving(SH)을 서브루틴으로 가지는 Hyperband의 의사코드

Hyperband

목적함수 f가 위와 같다면, 일반적으로 평가하는데에 지정된 하이퍼파라미터로 기계 학습 모델을 교육해야 하기 때문에 비용이 많이 들게 됩니다.. 대부분의 어플리케이션들은 budget b ∈ [bmin, bmax]에 의해 파라미터화 되는 f(·)의 저렴하게 평가할 수 있는 근사버전 ˜f(·, b)를 정의할 수 있습니다. 최대 budget b = bmax를 사용하면, ˜f(·, bmax) 즉, ˜f(·, bmax) = f(·)가 되는 반면, b < bmax를 사용하면 근사치에 머무르게 됩니다. 결국 일반적으로 budget b에 비례하는 것입니다. 본 논문에서는 이 budget을 이용하여 반복 알고리즘의 반복 횟수, 사용된 데이터 수, MCMC체인의 단계 수, 심층 강화 학습의 시행 횟수를 인코딩 합니다.

Hyperband(HB) (Li et al., 2017)은 하이퍼파라미터 최적화를 위한 멀티 암드 밴딧 전략입니다. 이는 무작위로 샘플링된 n개의 설정들 중에서 가장 좋은 출력을 얻기 위해, 각기 다른 budgets b에 대해 반복적으로 SuccessiveHalving(SH)(Jamieson & Talwalkar, 2016)을 호출함으로써 장점을 갖습니다. 알고리즘1에서 첫번쨰 라인은, 지리적으로 배치된 budget b ∈ [bmin, bmax]를 계산합니다. 3번째 줄에서, 샘플링된 설정들의 수는 모든 SH 실행에 요구된 전체 budget과 같은 숫자입니다. SH는 주어진 budget에서 구성을 내부적으로 평가하고, 성능에 따라 순위를 매긴다음, 계속적으로 η배 더 큰 budget에서 상위 η**-1에서(일반적으로 최대 3위까지)도 똑같이 평가합니다. 이 반복은 최대 budget에 이를때까지 진행됩니다. 실제로 HB는 매우 잘 작동하며, 일반적으로 중소 규모의 budget에 대해 전체 기능 평가 budget만 사용하는 Random search 및 Bayesian method보다 잘 작동합니다. 그러나, 전역 최적으로의 수렴은 무작위 추출 구성에 대한 의존성 떄문에 한계가 존재합니다. 또, Budget이 많을 수록 Random search보다 성능이 나빠질 수 있습니다.

4. Model_Based Hyperband

이제 Bayesian 최적화(BO)와 Hyperband(HB)를 결합한 BOHB라는 새로운 HPO방법을 소개합니다. BOHB는 서론에서 언급한 5가지 요구사항 외에도 두가지 사항을 더 만족합니다.

Simplicity

간단한 접근 방식으로, 쉽게 검증할 수 있고, 다른 프레임워크에서 쉽게 다시 구현이 가능합니다.

Computational efficiency

BOHB는 HB의 구성요소를 사용하여 적은 Budget으로 많은 기능 평가를 수행하게 될 수 있습니다. 이때, 표준 GPs(Gaussian Process)의 입방체 복잡성은 물론이고, 근사치 GPs의 낮은 복잡성또한 문제가 될 수 있습니다. 게다가, 이러한 복잡성은 보틀넥 현상을 부를 수 있습니다. 특히, 기능 평가의 비용을 효과적으로 줄이고자 할때 많이 발생합니다.

BOHB에서는 HB의 budget 선택 방식과 SH를 계속 사용하지만, 무작위 샘플링을 BO의 구성요소로 대체하여 탐색을 가이드 합니다. 지금까지 평가한 구성을 기반으로 모델을 구성하고, BO를 사용하여 새 구성을 선택합니다.

알고리즘2

BOHB의 샘플링 의사코드

BOHB의 BO부분은 TPE와 유사하지만 한가지 큰 차이점이 있습니다. 입력공간에서 상호 작용 효과를 더 잘 처리하기 위해 TPE에서 사용되는 1차원 KDE의 계층 구조가 아닌, 단일 다차원 KDE를 선택했습니다. 유용한 KDE를 맞추려면(알고리즘2의 4행에서) 최소 데이터 포인트 수 Nmin이 필요합니다.

4.1 Algorithm description

BOHB는 HB의 어떤 Budget에 얼마나 많은 설정구성을 평가할 것인지 정하는 메소드를 사용합니다. 그러나, HB는 무작위로 설정구성을 생성하는 반면에 BOHB는 모델을 기반으로 설정구성을 생성합니다. 원하는 수의 설정구성이 생성되면, 이 설정구성들에 대해 표준 Successive Halving프로시져가 수행됩니다. BOHB는 모든 budget b에 대한 설정구성x의 모든 함수평가 g의 성능을 기록하여 다음 반복에서 모델의 기초로 사용하게 됩니다.

HB처럼 budget선택과 SH를 사용하지만, 설정구성의 구성요소 선택에는 BO의 방식을 사용합니다. 새로운 설정구성을 생성할 때, 지금까지 평가한 설정구성으로 학습된 모델과 BO를 사용합니다. 이는 알고리즘2에서도 확인할 수 있습니다.

BOHB의 BO는 TPE와 비슷하지만 차이점이 있습니다. 본 논문에서는 입력공간에서 더 쉬운 상호작용 효과처리를 위해 한 차원의 계층형 KDE를 쓰는 TPE와는 다르게 하나의 다차원 KDE를 사용하였습니다. 유용한 KDE를 훈련시키기 위해서는 최소 데이터포인트 수 Nmin이 필요합니다 (line2, 본 연구에서는 하이퍼파라미터의 수 d + 1 입니다.). 모델을 최대한 빨리 생성하기 위해 Db를 Nmin + 2로 가정하고 (line 3)

각 모델의 최고 설정구성과 최악 설정구성을 선택합니다. 이렇게 하면 두 모델 모두 데이터 포인트가 충분하고 겹치는 부분이 최소화 됩니다. 또, statsmodels의 KDE를 사용했고, KDE의 대역폭을 평가했을 때, 효율적이면서 성능이 좋았다 (부록 D).

EI (line 5-6)를 최적화 하기 위해, 본 논문에서는 l'(x)에서의 Ns 포인트를 샘플링 했습니다. l'(x)는 l(x)와 같은 KDE이나, 더 가능성 있는 설정구성을 찾아내기 위해, 대역폭에 bw를 곱해 더 넓힌 KDE입니다. 본 연구에서는, 이 방법이 최적화의 후반단계, 특히 주기적으로 쿼리되지만 잘 업데이트 되지 않는 가장 큰 budget에서 설정구성 수렵을 향상시키는 것을 확인하였습니다.

HB을 이론적으로 보장하기 위해, 고정 비율 p도 무작위로 균일하게 샘플링합니다. 전역탐색 외에도, m · (Smax + 1) SH가 실행 된 후, 이 방법은 평균적으로 p · m · (smax+1)의 bmax의 랜덤 설정구성을 평가함을 보장합니다. 모든 SH 실행은 최대 (smax + 1) · bmax의 budget을 소비하지만 Random search는 (ρ**−1 · (smax + 1)), 즉, 2배 많은 구성을 평가합니다. 이는 최악의 경우 BOHB는 Random search보다 2배 느릴 수 있음을 보입니다. 그러나 결국 수렵하는 것이 보장되며, 실제로는 RS보다 성능이 뛰어났습니다.

4.2 Parallelization

최신 옵티마이저는 반드시 병렬 리소스를 최대한 활용할 수 있어야 합니다. BOHB는 TPE와 HB의 병렬성을 상속받기 때문에 이를 만족합니다. 먼저 TPE는 EI를 최적화 하기 위해, 샘플 수를 제한하고 의도적으로 완전히 최적화 하지 않았습니다. 이렇게 하면 병렬로 설정구성을 평가할 때, 모델의 연속적인 제안이 거의 선형에 가깝도록 다양해집니다. 또, HB는 각기 다른 반복을 동시에 시작하고, 각 SH실행 내에서 동시의 설정구성을 평가하는 방법으로 병렬화 할 수 있습니다.

BOHB의 병렬화 전략은 다음과 같습니다. 먼저, 순차적 HB가 수행할 첫번째 SH실행(가장 저렴한 budget부터 시작)하여 (a) 모든 작업자가 바쁘거나, (b) 충분한 설정구성이 생성됬을 때 까지 알고리즘2의 전략으로 설정구성을 샘플링 합니다. (a)의 경우, 간단하게 작업을 마친 작업자가 생길때까지 대기합니다. (b)의 경우, 다음 SH작업을 병렬로 시작합니다. 관찰 D에(결과 모델)은 모든 SH작업에서 공유됩니다. BOHB는 각 시점에서 최고의 검증 성능을 달성한 구성을 추적하는 상시 알고리즘 입니다. 이는 최대 budget이 주어진 SH 실행일 수 있습니다.

각 SH실행에 대해 별도의 작업자 풀을 생성하여 HB를 병렬화하는 기존의 방법과 달리, 작업자풀을 하나로 결합하고, 작업자가 사용 가능할 때마다 작은 budget을 우선적으로 실행합니다. 이 전략은 (a) 가장 공격적인(가장 효과적인) 계층의 모든 작업자를 먼저 사용하여 속도 향상을 달성하고, (b)적은 예산으로 구축된 모델을 최대한 활용하는 효과적인 방법을 보여줍니다.

그림2

128회 반복에 대한 BOHB의 여러 작업자 수별 성능 그래프.

5. Experiments

본 논문에서는 이제, 서포트벡터머신(SVM), 피드포워드 신경망, Bayesian 신경망, 심층 강화 학습 요원 그리고 합성곱신경망(CNN)의 하이퍼파라미터 최적화 및 광범위한 작업에서 BOHB의 경험적 성능을 종합적으로 평가해보겠습니다. 본 BOHB및 벤치마크용 코드는 https://github.com/automl/HpBandSter에서 공개적으로 사용할 수 있습니다.

• TPE와 비교하기 위해 Hyperopt 패키지 (Bergstra et al., 2011)사용
• 모든 GP-BO 방법에 대해 RoBO python패키지를 사용하였다. (Klein et al., 2017b)
• 모든 실험에서 HB 및 BOHB에 대해 η = 3을 사용하였다. (Li et al., 2017).
• 달리 명시되지 않은 경우, 모든 방법에 대해 주어진 Budget에서 현재 가장 잘 관찰된 설정구성의 평균 성능 및 표준오차를 표시한다.

5.1 Artificial Toy Function: Counting Ones

본 연구에서는 고차원 연속 / 비연속 혼합 설정구성 공간에서 BOHB의 동작을 연구했습니다. GP-BO 방법은 이러한 설정구성 공간에서 잘 작동하지 않기 때문에 (Eggensperger., 2013), 이 실험에서는 포함하지 않습니다.

주어진 범주형(비 연속형, Categorical)변수 Ncat, x ∈ {0, 1}와 연속형(Continuous) Ncont, x ∈ [0, 1] 에서 하나의 문제를 정의했습니다.

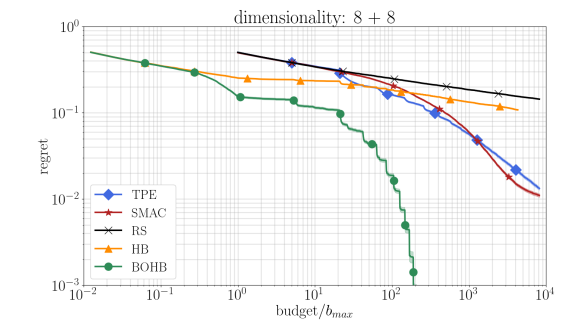
HB및 BOHB에 대한 Budget으로 b = 729를 가정했습니다. 또, 각 방법들마다 512회씩 독립적으로 실행하고, 각각의 regret을 보고합니다. 그림3은 Ncat=8 및 Ncont=8개의 파라미터가 있는 16차원 공간에서의 결과를 보여줍니다. 이 이외의 다른 차원에 대한 결과는 부록 H에서 확인할 수 있습니다.

Random search는 이 조건에서 제대로 작동되지 않았고, 초반에는 HB가 더 빨랐지만, 모델이 어느정도 학습한 이후에는 SMAC과 TPE가 확실히 더 좋은 성능을 보여주었습니다. BOHB는 HB와 같이 초반에도 성능이 좋았고, 이후에는 더 다른 방법들보다 좋은 성능을 보이며, 유일하게 특성 시간 Budget에 수렴되었습니다. 다른 차원들에서도 유사한 결과를 얻었으나, 차원이 64개이상 올라가면 BOHB의 노이즈가 증가하고, 적은 예산으로 설정구성을 평가하는 것이 더이상 효율적이지 않아, TPE 및 SMAC이 BOHB의 성능보다 높은 성능을 보이기 시작했습니다.

5.2 Comprehensive Experiments on Surrogate Benchmarks

다음 실험을 위해 본 연구에서는 Eggensperger et al.(2015)를 따라 오프라인 데이터를 기반으로한 대체 벤치마크 세트를 설계했습니다. 실제의 objective함수를 최적화 하는 것 보다 대체 함수를 최적화 하는 것이 훨씬 저렴하므로, 각 옵티마이저에 대해 다양한 독립적인 실행을 해볼 수 있고, 이를 통해 통계적으로 의미있는 결론을 도출할 수도 있습니다.

5.2.1 Support Vector Machine on MNIST

그림 4는 BOHB를 Fabolas(Klein et al., 2017a), multi-task(MTBO)(Swersky et al., 2013), 성능향상이 예상되는 GP-BO(Snoek et al., 2012; Klein et al., 2017b), RS 그리고 HB 입니다. BOHB는 Fabolas와 유사한 성능을 달성했으면, HB보다 더 잘 작동합니다.

5.2.2 Feed-Forward Neural Networks on OpenML Datasets

그림 5. HB는 처음 바닐라 BO방법 보다 훨씬 더 나은 성능을 보였고 RS보다 약 3배의 속도 향상을 달성했습니다. 그러나 Budget이 충분히 큰 경우, TPE와 GP-BO가 모든 경우에서 따라잡았습니다. 또한, BOHB도 HB와 동일하게 시작했지만, 최종 성능을 100배 더 빠르게 달성하였고, 동시에 다른 BO방법보다 더 나은 최종결과를 보였습니다.

5.3 Bayesian Neural Networks

이번에는 MCMC (Markob Chain Monte-Carlo) 샘플링으로 훈련된, 완전히 연결된 2개의 레이어를 가진 Bayesian 신경망의 아키텍처와 하이퍼파라미터를 최적화해보았습니다. 본 실험에서는 네트워크의 파라미터 벡터를 샘플링하기위해 확률적 그래디언트 Hamiltonian Monte-Carlo 샘플링(SGHMC) (Chen et al., 2014)과 스케일 적응(Scale adaption)(Springenberg et al., 2016)을 사용하였습니다. 현재(2018년), Bayesian 신경망을 위한 최초의 하이퍼파라미터 최적화의 시도입니다.

조정 가능한 하이퍼파라미터로,

• step length
• burn-in 주기의 길이
• 각 레이어의 유닛 수
• decay 파라미터의 momentum변수 (감쇠 파라미터의 운동량 변수)
  를 사용했습니다.
  본 연구에서는 Springerberg에서 설명한 대로(Springenberg et al., 2016), Bayesian 신경망구형에 RoBO 에서 제공하는 Python 패키지를 사용했습니다. (Klein et al., 2017b)

본 연구에서는 두 개의 다른 UCI(Lichman ,2013) 회귀(Regression)데이터셋을 고려했습니다. Boston bousing 데이터셋 과 Hernandez-Lobato와 Adams(2015) 의 Protein structure 데이터셋을 사용하였고, 검증데이터의 음의 로그유사도(Negative log-likelihood)를 확인하였습니다. HB와 BOHB의 경우, MCMC 단계에서 500의 최소 Budget을 주었고, 10000으로 최대 Budget을 설정했습니다. RS와 TPE는 최대 Budget에서 각각의 설정구성들을 평가합니다. 각각의 하이퍼파라미터 최적화 방법들은, 중요한 통계적 결과를 얻기 위해 각각 독립적으로 50회씩 실행했습니다.

그림 6에서 보듯, 초기엔 HB가 TPE보다 더 좋은 성능을 보였지만, 충분한 시간이 흐른 뒤에는, TPE가 더 빠른 성능을 보여주었습니다.
그림 6. SGHMC로 훈련된 Bayesian 신경망의 5가지 하이퍼파라미터 최적화. 최적의 하이퍼파라미터 설정 구성으로 갈 수록 음의 로그유사도(Negative log likelihoods)의 크기가 작아졌습니다.

5.4 Reinforcement Learning

다음으로, Cartpole swing-up 작업을 학습하기 위한 8가지의 Proximal Policy(근접 정책?) Opimization (PPO) (Schlman et al., 2017) 하이퍼 파라미터를 최적화 하였습니다. PPO의 경우, Schaarschmidt et al., (2017)이 개발한 TensorForce프레임워크를 사용하여 구현하였습니다. 또, OpenAI Gym(Brockman et al., 2016)도 cartpole환경 구현을 위해 사용되었습니다.

빠르게 수렴하며, 경고하게 작동하는 설정구성을 찾기 위해, 난수 생성기에 각기 다른 시드를 사용하여 생성한 9개의 설정 구성을 각각 평가했습니다. PPO가 최적의 설정으로 수렴될 때까지 평균 에피소드의 수를 반환했고, 강화학습 에이전트가 20개의 연속 에피소드에서 가장 높은 성적을 낼 때, 최적의 설정이라고 정의했습니다. 각 하이퍼파라미터 설정구성에 대해 에이전트가 한곳으로 수렴하거나, 최대 3000개의 에피소드에 도달할 때까지 학습을 진행했습니다. BOHB및 HB의 최소 Budget은 1로 시작하여 최대 9까지로 정의했고, 다른 모든 방법은 9로 고정했습니다. 또, 이전 벤치마크와 같이 각각 50회의 독립적인 반복을 진행했습니다.

그림7은 BOHB와 HB가 초기에는 비슷한 성능을 보였지만 결국 BOHB가 더 빠르게 수렴한 것을 볼 수 있습니다. 이때, 이 벤치마크의 Budget은 TPE가 제 성능을 발휘하기에는 너무 적었습니다.

5.5 Convolutional Neural Networks on CIFAR-10

마지막 평가를 위해, 본 연구에서는 중간 크기의 residual(잔차) 네트워크 (깊이 20, 너비 64, 약 8.5M개의 파라미터)와 Shake-Shake(Gastaldi, 2017) 및 Cutout(DeVries & Taylor, 2017)정규화를 사용했습니다. 하이퍼 파라미터 최적화를 위해 5000개의 훈련 이미지를 검증 이미지로 분리하였습니다. 또, 하이퍼파라미터로써, Learning rate, Momentum, Weight decay, Batch size를 최적화 했습니다.

본 연구에서는 19개의 worker를 병렬로 사용하여 22, 66, 200, 600번의 Epoch Budget으로 BOHB를 실행했습니다. 각 작업자는 2개의 1080 TI GPU를 사용했으며 최장 약 7시간이 걸렸습니다. 전체 BOHB의 16회 반복 실행에서는 총 33 GPU일이 필요했음, 2.78% +- 0.09%의 오류가 있었습니다 (Gastaldi (2017)의 더 큰 회로망보다 오류가 더 적었습니다.). 이럼에도 불구하고, 최신의 논문의 성능(2.4%, Reinforcement learning, Zoph et al., 2017)(2.1%, Evolutionary search, Real et al., 2018)보다 성능이 낮습니다. 그러나 이러한 방법은 제한된 자원에서의 최적화를 위한 BOHB방법보다 60~95배 더 많은 컴퓨팅 리소스가 필요하고, 3~4개 더 많은 매개변수가 존재하는 네트워크를 사용하기 때문에 BOHB방법은 더 실용적입니다.

6. Conclusion

본 논문에서는, 위에서 요약된 하이퍼파라미터를 최적화하는 간단하면서도 효과적인 방법인 HOBH를 소개했습니다. 강력하고 유연하며, 확장가능하고(고차원, 병렬 리소스), 강력한 항시 성능과, 높은 최종성능을 모두 달성합니다.

참고

https://simpling.tistory.com/52 (다양한 Hyperparameter Optimization 방법 리뷰)