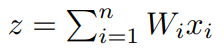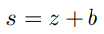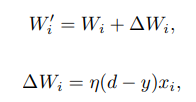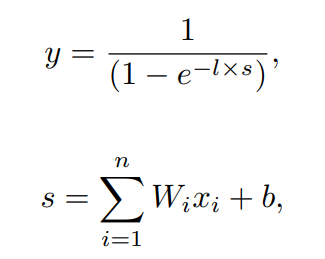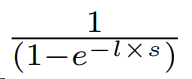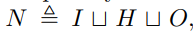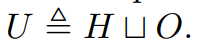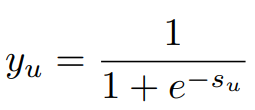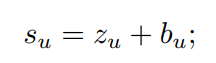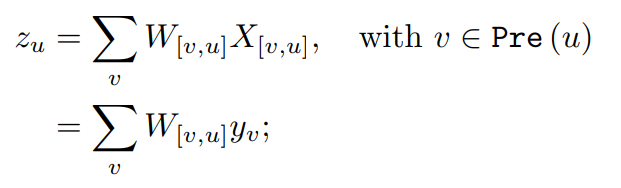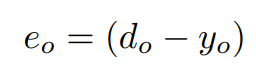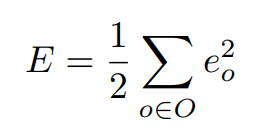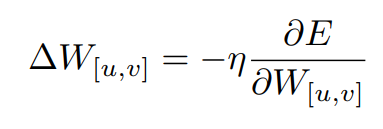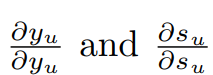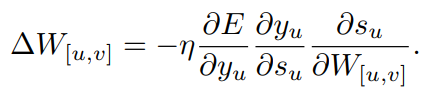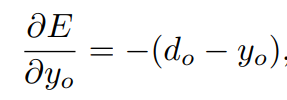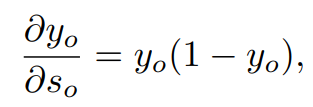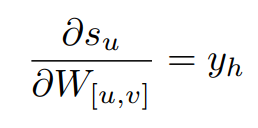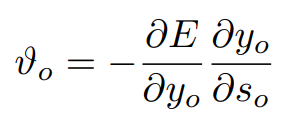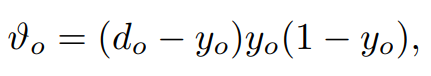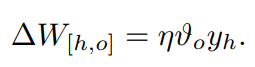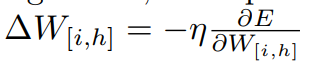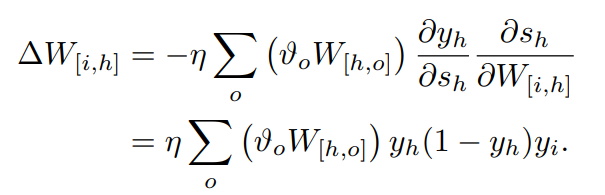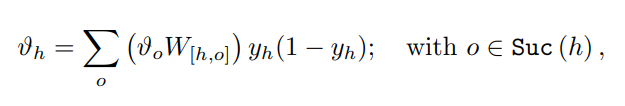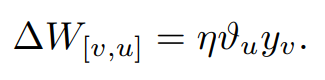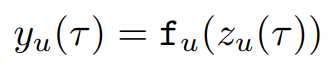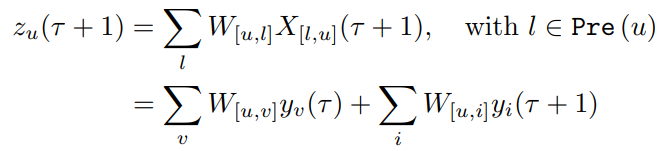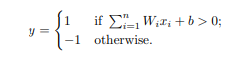
타이틀

– Understanding LSTM –

a tutorial into Long Short-Term Memory Recurrent Neural Networks

저자

Ralf C. Staudemeyer

Faculty of Computer Science
Schmalkalden University of Applied Sciences, Germany
E-Mail: r.staudemeyer@hs-sm.de

Eric Rothstein Morris

(Singapore University of Technology and Design, Singapore
E-Mail: eric rothstein@sutd.edu.sg)
September 23, 2019

1. Introduction

이 글은 LSTM-RNN(Long Short-Term Memory Recurrent Neural Networks)의 튜토리얼 형식의 소개글 입니다.

인공 신경망(ANN)은 뇌의 학습 시스템에서 영감을 받아 상호 연결된 뉴런의 복잡한 신경망을 모델링 한 것입니다. 뉴런은 실수 입력 벡터를 받아들이고, 단일 실수값의 출력을 생성하는 가장 간단한 단위입니다.

가장 일반적인 표준 신경망 유형은 피드 포워드 신경망입니다. 피드포워드 신경망은 하나의 입력레이어, 하나의 출력레이어 및 하나 이상의 중간 hidden 레이어로 구성됩니다. 이 피드 포워드 신경망은 정적 분류만 가능하며, 시간 예측 작업을 모델링 하려면 동적인 분류가 가능해야 합니다. 따라서, 피드 포워드 신경망을 동적으로 확장하여, 이전 시간 단계의 신호를 현재 네트워크로 다시 공급하는 순환 연결 네트워크가 개발되었고 그것이 RNN(Recurrent Neural Networks)입니다.

RNN은 약 10개의 과거 데이터만 가져올 수 있습니다. 피드백된 신호가 사라지거나 폭발하기 때문입니다. 이 문제를 해결하기위해 나온것이 LSTM-RNN(Long Short-Term Memory Recurrent Neural Networks)네트워크 입니다. LSTM은 구축된 네트워크에 따라 1,000개 이상의 과거 시간 단계를 학습할 수 있습니다.

2. Notation

본 논문에서는 다음 표기법을 사용합니다.

• 네트워크의 학습률은 η입니다.
• 시간 단위는 τ 입니다. Epoch의 초기 시간은 t 0으로 표시되고 마지막 시간은 t로 표시됩니다.
• 네트워크의 단위 집합은 N이고 일반(달리 명시되지 않는 한) 단위는 u, v, l, k ∈ N입니다.
• 입력 단위 집합은 I이고 입력 단위는 i ∈ I입니다.
• 출력 단위 집합은 O이고 출력 단위는 o ∈ O입니다.
• 비입력 단위의 집합은 U입니다.
• 단위 u(u의 활성화라고도 함)의 출력은 yu이며 입력과 달리 단일 값입니다.
• 유닛 u에 연결된 유닛 세트; 즉, 그 전임자는 Pre(u)
• 유닛 u에서 연결되는 유닛 세트; 즉, 그 후계자는 Suc(u)입니다.
• 단위 v와 단위 u를 연결하는 무게는 W[v,u]입니다.
• 단위 v에서 오는 단위 u의 입력은 X[v,u]로 표시됩니다.
• 단위 u의 가중치 입력은 zu입니다.
• 단위 u의 바이어스는 bu입니다.
• 단위 u의 상태는 su입니다.
• 단위 u의 스쿼싱 기능은 fu입니다.
• 단위 u의 오차는 eu입니다.
• 단위 u의 오차 신호는 ϑu입니다.
• 가중치 W[u,v]에 대한 단위 k의 출력 감도는 p k uv입니다.

3. Perceptron and Delta Learning Rule

3.1 The Perceptron

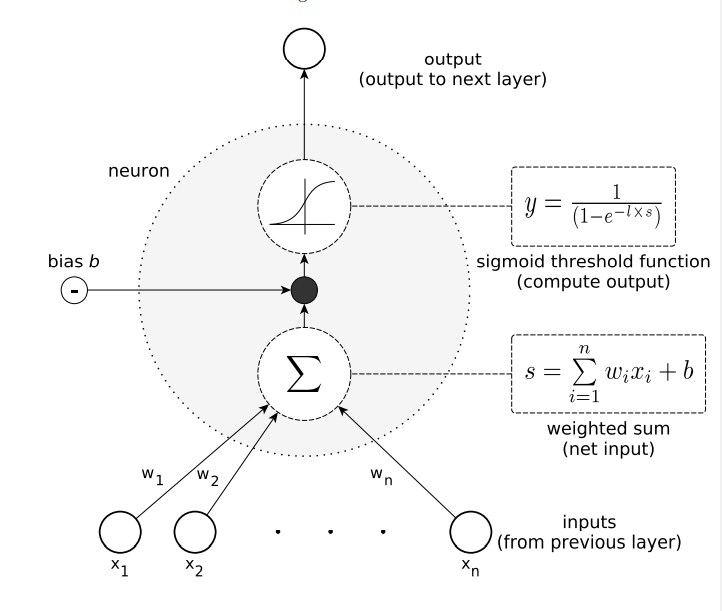
인공 뉴런의 가장 기본적인 유형은 퍼셉트론(perceptron)이라고 합니다. 퍼셉트론은 여러 외부 입력 링크, 임계값 및 단일 외부 출력 링크로 구성됩니다. 또, 퍼셉트론에는 바이어스라고 하는 내부 입력 b가 있습니다. 퍼셉트론은 실수입력값 벡터를 사용하며, 모두 제곱으로 가중치가 부여됩니다.

이전 퍼셉트론 훈련 단계에서, 퍼셉트론은 훈련 데이터를 기반으로 이러한 가중치를 학습합니다. 모든 가중 입력값을 합산하고, 결과 값이 미리 정의된 임계값을 초과하면 'fire(실행)'됩니다. 퍼셉트론의 출력은 한상 boolean값이며, 출력이 '1'이면 실행된 것으로 간주합니다. 또, 비활성화시 '-1'이며 대부분의 경우 '0'입니다.

입력 벡터 x = (x1, ..., xn)과 훈련된 가중치 W1, ..., Wn이 주어지면, 퍼셉트론은 y를 출력합니다. 이는 다음과 같습니다.

여기서 우리는 Wixi의 1부터 n가지의 합을 가중치 입력(weighted input)으로,

z와 b의 합을 퍼셉트론의 상태로 참조합니다.

즉, 퍼셉트론이 작동하려면, 상태 s가 임계값을 초과해야 하는 것입니다.

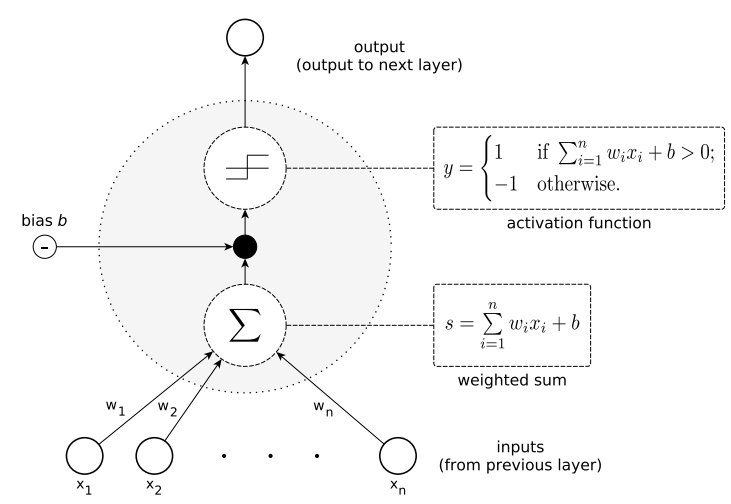
단일 퍼셉트론 유닛은 이미 많은 유용한 기능을 보여줍니다. 예로, AND, OR, NAND, NOR같은 bool연산을 처리할 수 있습니다. 단일 퍼셉트론은 선형으로 분리 가능한 함수만 학습할 수 있습니다. 일반적인 퍼셉트론의 구조는 아래와 같습니다.

• Figure 1: 퍼셉트론이라고 하는 가장 기본적 유형의 인공 뉴런의 일반적인 구조.

3.2 Linearay Separability

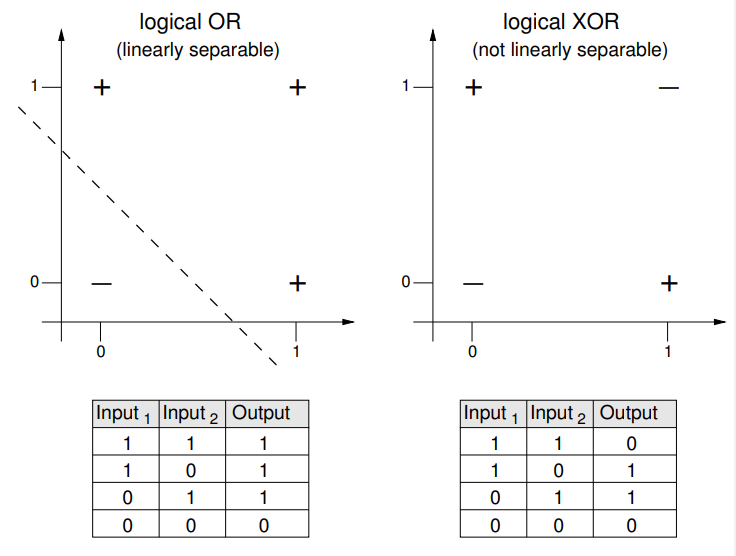
단일 퍼셉트론은 선형으로 분리 가능한 함수를 학습하는 것으로 제한되어있다. 라고 했지만, 선형 분리 가능성을 이해하려면, 2차원 그래프에서 퍼센트론이 받아드릴 수 있는 입력을 시각화하는 것이 좋습니다. 그림2는 bool함수 OR과 XOR를 보여줍니다. OR함수는 선형으로 분리할 수 있지만, XOR함수는 그렇지 않습니다. 그림에서 +는 퍼셉트론이 동작하게되는 입력에 사용되고, -는 작동하지 않는 입력에 사용된니다. +와 -를 한줄로 완전히 분리할 수 있다면, 이 문제는 2차원에서 선형으로 분리할 수 있습니다. 따라서, 훈련된 퍼셉트론의 가중치는 그림의 실선을 나타낼 것 입니다.

• 그림2: bool함수 OR과 XOR의 표현. OR는 선형으로 분리할 수 있지만, XOR은 분리하지 못한다.

3.3 The Delta Learning Rule

퍼셉트론 훈련은 모방에 의한 학습이며, 우리는 이를 '지도 학습' 이라고 합니다. 훈련 단계에서 퍼셉트론은 output을 생성하고 이를 훈련데이터의 output값과 비교합니다. 만약, 퍼셉트론의 출력값이 틀렸다면, 그에따라 가중치를 수정합니다.

현재 퍼셉트론에 대한 다양한 훈련 알고리즘이 존재하며, 그 중 가장 일반적인 것은 퍼셉트론 학습 규칙과 델타 학습 규칙입니다. 둘 다 무작위 가중치로 시작하며, 둘다 수용 가능한 가설로 수렴을 보장 합니다. 퍼셉트론 학습 규칙 알고리즘을 사용한다면, <x, d> 샘플 쌍을 이용하여 학습할 수 있습니다(이떄 x는 주어진 input, d는 label). 샘플 쌍 <x, d>의 경우, input x = <x1, ..., xn>, 이전 가중치 W = <W1, ..., Wn>일때, 새로운 가중치 벡처 W'는 다음과 같습니다.

또, 여기서 y는 input x와 가중치 W를 사용하여 계산된 출력이고, η은 learning rate입니다..
learning rate는 가중치가 변경되는 정도는 제어하는 상수입니다. 앞서 언급한 것과 같이, 초기 가중치 W0는 임의의 값을 가집니다. 알고리즘은 훈련 데이터가 선형으로 분리 가능하고, 학습률이 충분히 작을 때, 최적으로 수렴합니다. 만약 학습 예제가 선형으로 분리되지 않는다면 퍼셉트론 규칙이 실패하게 됩니다.

델타 학습 규칙은 선형으로 분리 가능한 훈련과 선형으로 분리할 수 없는 훈련 예제를 처리하도록 특별이 설계되었습니다. 또 퍼셉트론 학습 규칙과 같이, 계산된 출력과 훈련 샘플의 출력 데이터 사이의 오류를 계산하고 그에따라 가중치를 수정합니다. 가중치 수정은 그래디언트 최적화 하강 알고리즘을 사용하여 달성되며, 이는 전역 최소 오차를 향해 오차 표면을 따라 가장 가파른 하강을 생성하는 방향으로 가중치를 변경합니다. 이 델타 학습 규칙은 이 섹션의 뒷부분에서 논의할 Error Backpropagation algorithm (오류 역전파 알고리즘)의 기초가 됩니다.

3.4 The Sigmod Threshold Unit

Sigmod Threshold Unit은 퍼셉트론과는 유사하지만 다른, 출력을 계산할 떄, sigmod함수를 사용하는 인공신경입니다. 출력 y는 다음 공식으로 계산 됩니다.

여기서 b는 편향이고 ㅣ은 sigmod함수의 기울기를 결정하는 양의 상수입니다. 이 sigmod함수의 주요 효과는 Sigmod Thresholc Unit은 두개 이상의 값이 가능하다는 점입니다.

위 함수에 의해 출력값이 0~1사이로 squashed(눌려짐)되기 때문에 squashing함수라고 합니다.
퍼셉트론은 선형으로밖에 함수를 나타내지 못했지만, Sigmoid unit을 사용하는 신경망은 비선형 함수도 표현할 수 있습니다.

• 그림3: Sigmoid Threshold Unit은 비선형 함수를 표현할 수 있습니다. 또, 출력은 입력의 연속적인 함수이며, 0~1사이의 값입니다.

4. Feed-Forward Neural Networks and Backpropagation

피드포워드 신경망(FFNN)에서 뉴런 세트는 레이어로 구성되며, 각 뉴런은 입력의 가중치 합을 계산합니다. 이중, 환경과 직접적으로 연결되어있지 않고, 다른 뉴런끼리만 연결되어있다면, 이를 hidden neuron이라고 합니다.

피드포워드 신경망은 루프가 존재하지 않고, 완전 연결되어있습니다. 이는 각 뉴런은 다음계층에만 출력을 제공하지, 이전 계층으로는 출력을 제공하지 않음을 의미합니다.

가장 간단한 단일 레이어 퍼셉트론 네트워크에서는 input layer(input neurons)과 output layer(output neurons)로 구성됩니다.

모든 단일 퍼셉트론은 가중치와 입력의 곱의 합을 계산합니다. 만약 임계값보다 높으면 1, 아니면 -1을 출력하고, 임계값은 일반적으로 0을 사용합니다.

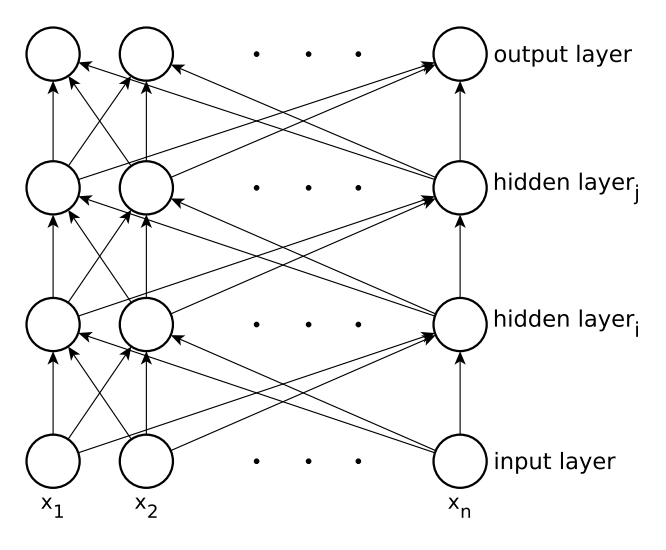
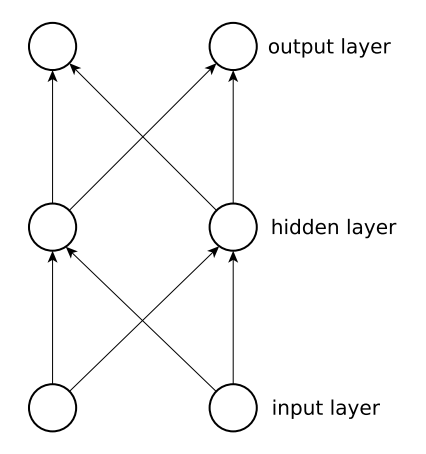
여러 계층으로 구성된 뉴런들로 여러 layer를 가진 네트워크를 형성할 수 있습니다. 이때, input layer는 하나 이상의 hidden layer를 통해 output layer와 연결됩니다. 1개의 input layer와 3개의 output layer (2개의 hidden layer, 1개의 output layer)가 있는 그림4의 피드포워드 신경망은 3층 피드포워드 신경망으로 불립니다.

다만 대부분의 문제에서 2개 이상의 레이어가 있는 피드포워드 신경망은 이점이 없습니다. 그래서 sigmoid threshold unit 함수를 사용하는 다층 피드포워드 신경망을 사용합니다. 이때, hidden unit이 충분하다면 모든 함수는 이 네트워크를 통해 근접하게 근사될 수 있습니다.

• 그림 4: 입력레이어 1개, 은닉(hidden)레이어 2개, 출력 레이어 1개가 있는 다층 피드포워드 신경망. 시그모이드 임계값 기능이 있는 뉴런을 사용하여 이러한 신경망은 비선형 결정 표면을 표현할 수 있습니다.

가장 일반적인 신경망 학습기술은 오류 역전파 알고리즘(Error backpropagation algorithm) 입니다. 오류 역전파 알고리즘은 경사하강법(gradient descent)을 사용하여 다층 네트워크에서 가중치를 학습합니다. 출력레이어에서 입력레이어쪽으로 역방향으로 진행하면서 작은 반복단계를거쳐 작동합니다. 이때 뉴런의 활성화 기능이 미분 가능해야 한다는 것 입니다.

오류 역전파는 모든 훈련 샘플을 신경망에 적용하고 모든(hidden 포함) 출력 레이어에 대한 각 Unit의 입력 및 출력을 계산합니다.

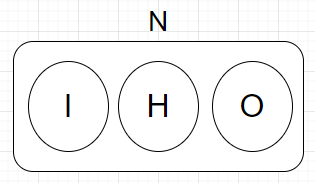
네트워크의 단위집합 N은 입력 I, 은닉 H, 출력 O의 분리 합집합으로 표현할 수 있습니다. 또한 각 유닛은 소문자로 표현해, 입력유닛 i, 은닉유닛 h, 출력유닛 o로 표현합니다.

편의를 위해 입력이 아닌 비입력 집합은 U로 정의하고, 비입력 유닛 u ∈ U의 경우, u에 대한 입력은 xu, 상태는 su, 바이어스는 bu, 출력은 yu로 표시됩니다. 주어진 유닛 u와 v를 연결하는가중치는 Wuv로 표시죕니다.

외부 입력을 모델링하기 위해, 외부입력벡터 x = <x1, ..., xn>을 사용합니다. 외부 입력 벡터의 각 요소는 이를 모델링하는 해당 입력 유닛을 찾게된다. 따라서, i번째 입력유닛의 출력은 네트워크에 대한 입력의 i번대 구성요소(xi)와 같아야하며 결과적으로 |I| = n이다.

비입력 유닛 u에 대해, 출력 u, 쓰여진 u 은 다음 시그모이드 활성화 함수를 통해 정의됩니다.
(1)
비입력 유닛 u에 대한 상태 su는 다음과 같이 정의됩니다.
(2)
비입력 유닛 u에 대한 바이어스 bu, 가중치 입력 zu는 다음과 같이 정의된다.
(3)
여기서 X[v,u]는 v가 u에 대한 입력으로 전달하는 정보이고, Pre(u)는 u에 오는 유닛집합 v입니다. 즉, 입력유닛과 출력 yv(방정식 1 참조)에 가중치 W[v,u]를 곱하여 유닛 u에 공급하는 은닉 유닛입니다.

입력 레이어부터 시작해, 출력 레이어에 도착할 떄까지, 입력은 네트워크를 통해 앞으로 전파됩니다. 이후, 출력유닛은 관찰 가능한 출력(네트워크 출력) y를 생성합니다. 자세하게는, o가 O의 원소일 떄, yo는 y의 o번째 구성요소에 해당합니다.

다음으로, 역전파 학습 알고리즘은 오류를 역방향으로 전파하고, 가중치와 biases(편향)을 수정하여 현재 훈련 샘플에 대한 오류를 줄입니다. 출력 레이어에서 시작하는 역전파 학습 알고리즘은, 네트워크 출력 yo를 목표하는 출력 do와 비교합니다. 각 출력 뉴런들은 몇가지 오류함수를 사용해 최소화해야하는 에러 eo를 계산합니다. 이때, 오류 eo는 다음과 같이 계산됩니다.

그리고 네트워크 오류에 대한 공식이 있습니다.

가중치 W[u,v]를 얻기 위해, 다음 공식을 사용합니다.

여기서 η은 학습률(learning rate)를 말합니다.

우리는 이제 위 두가지 요소를 사용하여 활성화 오류를 유도하고, 상태 활성화를 유도하고, 순서대로 가중치에 대한 상태의 미분을 유도하여 수정할 가중치를 계산합니다.

출력 유닛의 활성화과 관련된 오류의 미분은 다음과 같습니다.

이제, 출력 유닛의 상태 활성도의 미분은 다음과 같습니다.

그리고, 은닉 유닛 h를 출력 유닛 o에 연결하는 가중치에 대한 상태의 미분은 다음과 같습니다.

출력 유닛 o의 오류 신호를 다음과 같이 정의합니다.
(4)
우리가 가진 출력 유닛의 경우
(5)

은닉 유닛 h와 출력 유닛 o사이의 가중치를 다음과 같이 업데이트 할 수 있습니다.

이제, 은닉유닛 h에 대해, 만약 우리가 네트워크 오류가 얼마나 에러출력에 기여하는지 고려한다면, 은닉유닛 h가 신호를 보내는 출력유닛에서 오류를 역전파 할 수 있습니다. 정확하게는, 입력유닛 i에 대해 방정식을 다음과 같이 확장해야 합니다.
(입력유닛 i)

(확장)

• 그림5: 이 그림은 피드포워드 신경망을 나타낸다.

우리가 은닉유닛 h의 오류 신호(Error signal)를 정의한다면,

그 다음, 우리는 이미 가중치 변화량에 대한 표현식이 있습니다.

이렇게 모든 네트워크 출력이 허용 가능한 범위에 있거나, 다른 종료 조건에 도달할 때 까지 가중치 변화량 ∆W[v,u]를 반복해서 계산합니다.

5. Recurrent Neural Networks (RNN)

순환신경망(RNN, Recurrent Neural Networks)은 분류의 각 단계마다 내부 상태가 있는 동적 시스템 입니다. 이는 RNN이 상위 레이어와 하위 레이어 뉴런사이의 순환 연결 및 선택적 자체 피드백 연결을 가질 수 있도록 합니다. 이러한 피드백 연결을 통해 RNN은 과거 이벤트에서 현재의 처리단계로 데이터를 전파할 수 있습니다. 그렇기 떄문에 RNN으로 시계열 이벤트의 메모리를 구축할 수 있습니다.

5.1 Basic Architecture

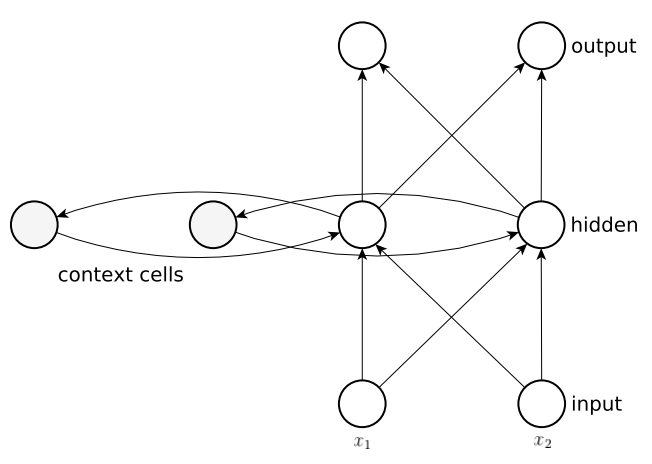
Elman 네트워크는 기존 3계층 신경망과 유사하지만, 추가적으로 은닉계층의 출력이 컨텍스트 셀이라는 곳에 저장됩니다. 컨텍스트 셀의 출력은 원래 신호와함꼐 은닉뉴런에 순환적으로 피드백 됩니다. 또, 모든 은닉뉴런에는 자체 컨텍스트 셀이 있으며, 입력 레이어와 자체 컨텍스트 셀, 두 곳에서 입력을 받습니다. Elman네트워크는 표준 오류 역전파로 훈련될 수 있으며, 컨텍스트 셀의 출력은 단순히 추가 입력으로만 간주됩니다. 위에서 보여주었던 그림 5와 아래 그림 6은 이러한 Elman네트워크와 표준 피드포워드 네트워크를 비교합니다.

• 그림6: Elman neural network
  
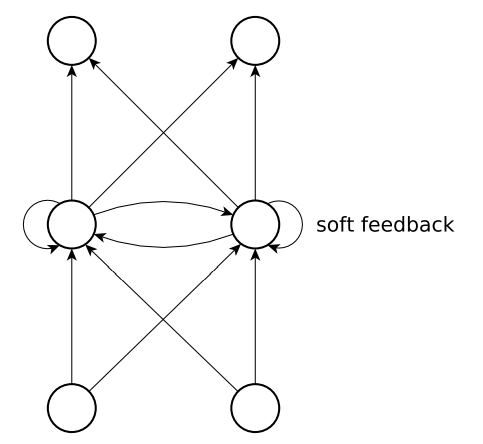
• 그림7: 은닉레이어에 자체 피드백이 있는 부분 반복 신경망
  
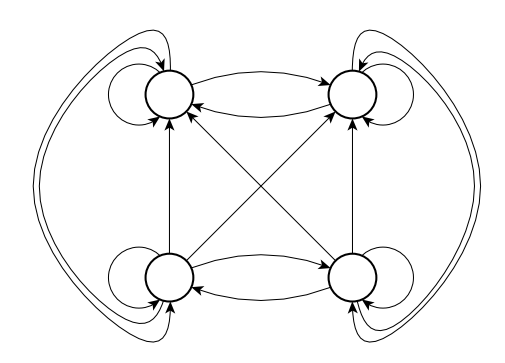
• 그림8: 자체 피드백 연결이 있는 완전 순환 신경망(RNN)

Jordan 네트워크는 Elman 네트워크와 유사한 구조를 가지고 있지만, 컨텍스트 셀이 출력 레이어에서 공급된다는 차이점이 있습니다. 그림 7에서 완전히 연결된 은닉 레이어가 있는 부분 순환 신경망을 보여줍니다. 또, 그림 8에서 완전히 연결된 RNN을 보여줍니다.

RNN은 섹션 4.Feed-Forward Neural Networks and Backpropagation과는 다르게 학습되어야 합니다. RNN은 단계 간 반복 연결을 통해 정보를 전파해야 하기 때문입니다. RNN을 학습시키기 위한 가장 일반적이고 잘 알려진 학습 알고리즘은 시간을 통한 역전파(BPTT, Backpropagation Through Time) 및 실시간 순환 학습(RTRL, Real-time Recurrent Learning)입니다. BPTT에서 네트워크는 FFNN을 구성하고 가중치에 일반화된 델타규칙이 적용됩니다. 이는 먼저 데이터를 수집한 후에 모델을 구축한다는 점에서 오프라인 학습 알고리즘입니다. RTRL은 그래디언트 정보가 순방향 전파됩니다. 여기서, 데이터는 시스템에서 온라인으로 수집되며, 수집과 동시에 모델이 학습됩니다. 따라서 RTRL은 온라인 학습 알고리즘 입니다.

6. Training Recurrent Neural Networks

위에서 언급했듯이 순환 신경망을 훈련시키는 가장 일반적인 방법은 BPTT(Backpropagation Through Time)과 RTRL(Real-Time Recurrent Learning)입니다. BPTT와 RTRL의 주요 차이점은 가중치 변화가 계산되는 방식입니다. LSTM-RNN의 원래 공식은 BPTT와 RTRL의 조합입니다. 따라서 이 두가지 학습 알고리즘을 간단히 살펴봅시다.

6.1 Backpropagation Through Time

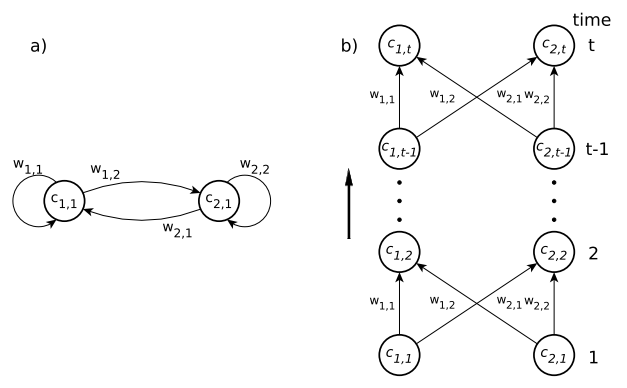
• 그림9 : 그림 a는 2개의 뉴런 레이어가 있는 간단한 완전 순환 신경망을 보여줍니다. 그림 b는 피드포워드 신경망으로, 각 시간 단계에 대해 별도의 계층을 사용하여 시간이 지남에 따라 펼쳐지는 동일한 네트워크가 나와 있습니다.

BPTT알고리즘은 일정 기간동한 모든 RNN에 대해 동일한 동작을 하는 FFNN이 있다는 사실을 이용합니다. 이 FFNN을 얻으려면 시간내에 RNN을 펼쳐야 합니다. 그림 9a는 단일 2개의 뉴련 레이어가 있는 단순하고 완전 순환되는 신경망를 보여줍니다. 그림 9b에 표시된 피드포워드 신경망은 모든 계층에 대해 동일한 가중치를 가진 각 시간 단계에 대해 별도의 계층이 필요합니다. 만약 가중치가 RNN과 동일하다면, 두 네트워크는 모두 동일한 동작을 보일 것 입니다.

펼쳐진 네트워크는 섹션 4에서 설명한 역전파 알고리즘으로 훈련할 수 있습니다. 훈련시퀀스가 끝나면 네트워크가 제 시간에 펼쳐집니다. 사용자가 선택한 특정 오류 측정방법을 이용하여, 실제 목표 값이 있는 출력유닛에 대해 오류가 계산됩니다. 그런다음 오류가 네트워크에 거꾸로 주입되고, 모든 시간 단계에 대한 가중치 수정이 계산됩니다. 순환 네트워크 버전의 가중치는 모든 시간 단계에서 델타의 합으로 업데이트 됩니다.

반복 역전파 알고리즘을 사용하여 단일 패스의 모든 시간단계의 오류 신호를 계산합니다. 번수 τ로 인덱싱된 시간단계를 정의합니다. 네트워크가 t0에서 시작하고 t에서 끝난다고 할 떄, t0와 t사이의 프레임을 에포크(epoch)라고 합니다. 또, U를 비입력 유닛의 집합이라 하고, fu를 미분가능한 비선형 스쿼싱 함수라고 합니다. 또한, yu(τ)를 시간 u에서의 출력이라고 정의합니다.

τ는 다음과 같이 주어집니다.

가중치 입력으로

여기서 v는 비입력집합 U와 Pre(u)의 교집합이고, i는 입력 유닛 집합입니다. 시간 τ + 1에서 u에 대한 입력은 두 가지 유형입니다. 입력유닛을 통해 시간 τ + 1에 도착하는 환경 입력과, 시간 τ에서 생성된 네트워크 모든 비입력 유닛의 반복 출력. 만약 네트워크가 완전히 연결되었다면 비입력집합 U와 Pre(u)의 교집합은 비입력집합 U와 같습니다. T(τ)를 시간 τ에서 출력값