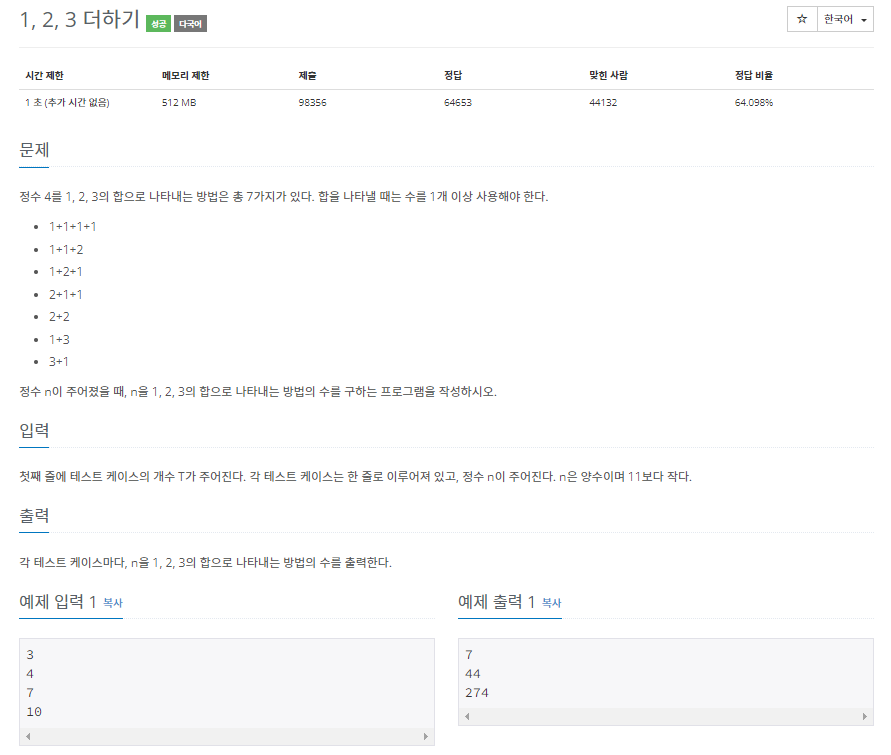
DP문제이다. 처음 접근하면 비교적 어렵다.
먼저 문제를 해결하려면 규칙성을 발견하고 점화식 도출해야 한다.
✅점화식 도출
예를 들어, n=1, n=2, n=3일 때의 경우의 수를 구해보면 다음과 같다.
n=1: 1
n=2: 1+1, 2
n=3: 1+1+1, 1+2, 2+1, 3
여기서 n=4의 경우의 수를 구하려면, n=1, n=2, n=3일 때의 경우의 수를 이용할 수 있다.
따라서, n=1일 때의 경우의 수인 1에 3을 더한 경우,
n=2일 때의 경우의 수인 2에 2를 더한 경우,
n=3일 때의 경우의 수인 3에 1을 더한 경우를 더해주면 된다.
n=4: 1+1+1+1, 1+1+2, 1+2+1, 1+3, 2+1+1, 2+2, 3+1
이와 같은 방식으로, n=5일 때의 경우의 수를 구할 수 있다. 이를 점화식으로 나타내면 다음과 같다.
dp[1] = 1
dp[2] = 2
dp[3] = 4
dp[j] = dp[j-1] + dp[j-2] + dp[j-3] (j >= 4)✅코드
import java.io.*;
public class Main{
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int n = stoi(br.readLine());
int dp[] = new int[11];
dp[1] = 1;
dp[2] = 2;
dp[3] = 4;
for(int i = 4; i < 11; i++)
dp[i] = dp[i-1] + dp[i-2] + dp[i-3];
for(int i = 0; i < n; i++){
int t = stoi(br.readLine());
sb.append(dp[t] + "\n");
}
System.out.println(sb);
}
public static int stoi(String str) {return Integer.parseInt(str);}
}.jpg)