프로그래밍언어 수 표현방식
정수타입, 실수 타입 이 두가지가 있다.
정수
java의 정수 자료형으로는 byte, short, int, long이 있으며, java는 모든 정수를 4바이트를 처리하고 만약 초과시 long으로 처리를 한다.
// 표현범위 예시
byte bs = -128 ; // -128 ~ 127
long iVal = 12345678900L; // int시 too large - > –2,147,483,648 ~ 2,147,483,647실수
실수를 표현할 때는
- 부동 소수점 방식(실수 표현시, 소수점의 위치를 고정하지 않는 것),
- 고정 소수점 방식((실수 표현시, 소수점의 위치를 고정)이 있다.
하지만 대부분 부동소수점 방식을 쓴다.
고정 소수점
123.456이라는 수 표현시! -> 정수 부분 123과 소수 부분 456을 나눠서 표현
한정된 비트에 정수와 소수 부분을 분할해 배치할 경우 고정소수점이 나타낼 수 있는 범위가 무척 한정
부동소수점(2진법)


- 컴퓨터에서는 밑수가 2 이므로 정규화를 하게 되면 가수부분의 첫 번째 자리 숫자는 항상 1임
ex) 0.2 표현-> 0.4 X 2^-1 정규화 하면 1.6 X 2^-3
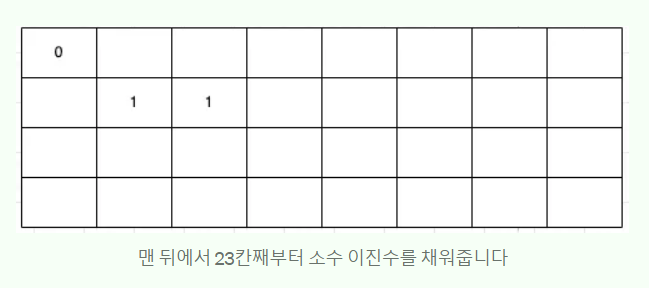
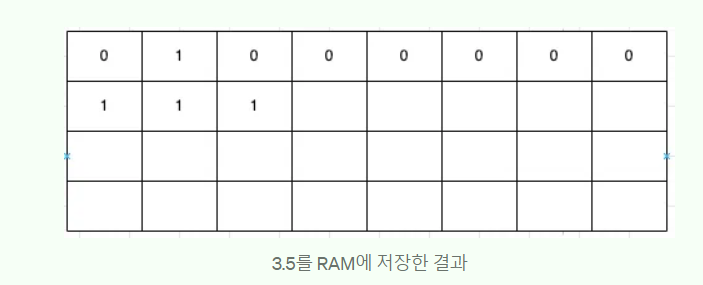
3.5를 이진수로 표현해보자!
- 3.5를 이진법으로 변환해서 11.1 이란 이진수로 변환
- 소숫점을 왼쪽으로 끝까지 이동시켜 1.11
- 이진수 1.11에 왼쪽으로 이동한 만큼 2를 곱해주면 원래 수인 3.5가 되는 것
그다음 남은 이진수 1을 십진수로 변환한 다음 127을 더해준 후 이 결과를 이진수로 변환2 + 127 = 129 129를 이진수로 변환 => 10000001나머지 8칸에 10000001을 넣어주면
하지만 소수점 0.1 -> 2진법으로 표현하면 0.0001100110011001… 이렇게 딱 떨어지지 않고 순환소수가 되버린다..
이러면 어떤 문제가 생기는가..
부동소수점 순환소수 예시
public class DoubleTest {
public static void main(String[] args) {
double dNum = 3.14; // 8byte
float fNum = 3.14f; //4byte
System.out.println("dNum = " + dNum);
System.out.println("fNum = " + fNum);
// 부동 소수점 오류!!
double mynum = 1;
for (int i = 0; i < 10000; i++) {
mynum = mynum + 0.1;
}
System.out.println("mynum = " + mynum); /// 출력값 1001.000000000159
// 오차 0.000000000159
}
}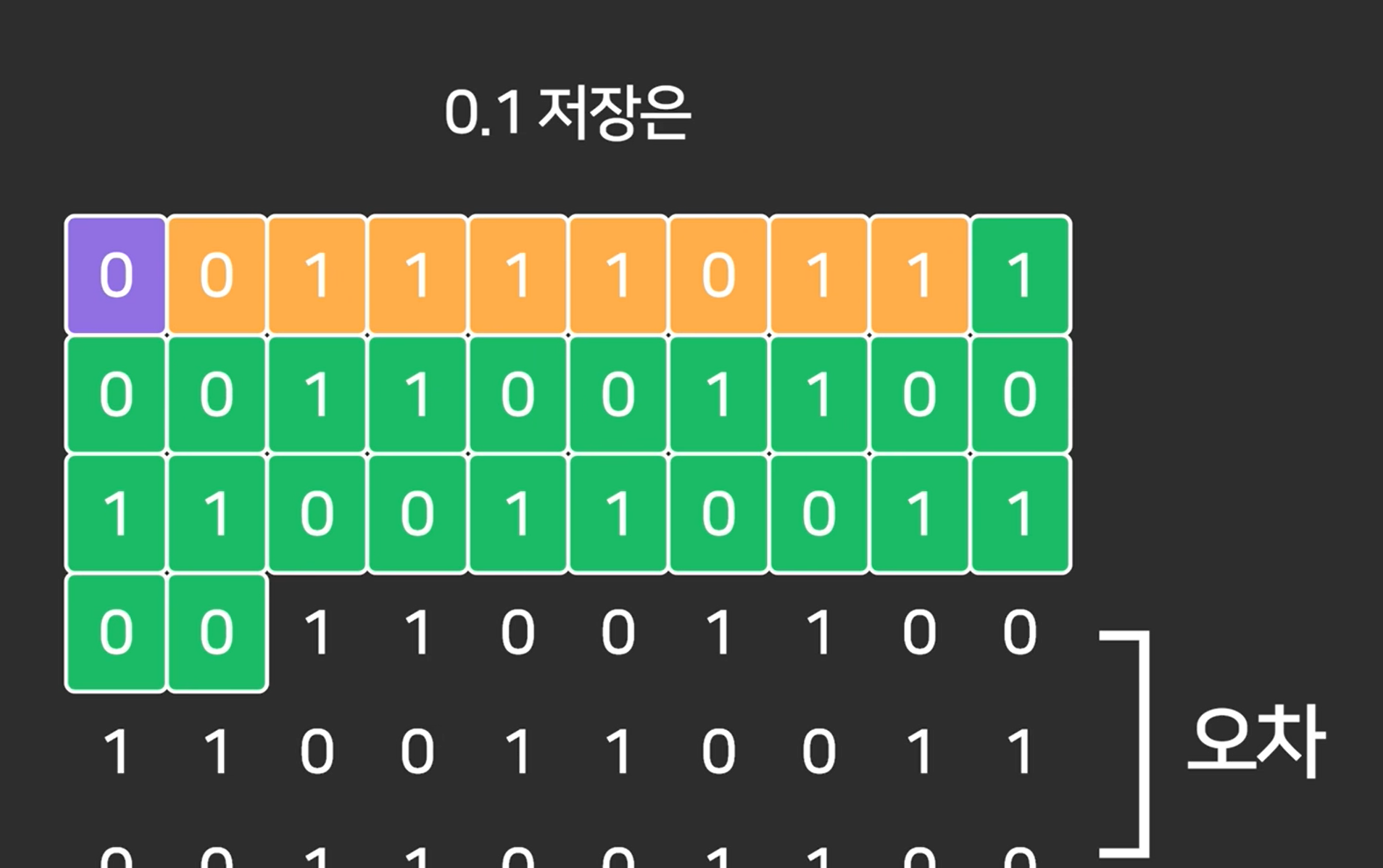
즉! 0.1을 저장하더라도 0.1과 비슷한 수를 저장하는 것...
ex) 0.010011001100110은 정확히 0.3을 나타낼 수는 없습니다. 10진수로 나타내 보면 0.29998779296875을 나타냅니다.
그래서 부동 소수점을 어떻게 처리하지?
- 정확한 계산을 하려면 정수처리를 하자..
- 3.2 -> 3200으로 만들어서 연산
- 반올림 문법
- double 자료형 -> 즉 자료저장칸을 더 늘린다는 것(64bit)
이해한다면
overflow현상, Not a Number, Infinity도 검색해서 보자!