🟡 라쏘 회귀란?
→ 라쏘 회귀는 선형 회귀의 또 다른 규제된 버전
릿지 회귀처럼 비용 함수에 규제항을 더하지만 릿지 회귀와 다르게 가중치 벡터 노름을 사용한다.
🟨 라쏘가 등장한 이유
: 릿지 회귀는 모든 p개의 변수를 포함하고 패널티 항은 모든 계수가 0이 되는 방향으로 수축한다. 람다가 무한이 아닌 경우에 계수를 정확히 수축하지 않는다. 모델의 정확도 관점에서는 문제가 되지 않지만 모델을 해석해야 하는 경우 문제점이 발생할 수 있기 때문에 Lasso 가 등장하였다.
라쏘 회귀의 비용 함수
-라쏘 회귀의 중요한 특징은 덜 중요한 특성의 가중치를 제거하려고 하는 것 ( 가중치가 0 이 된다는 뜻 !)
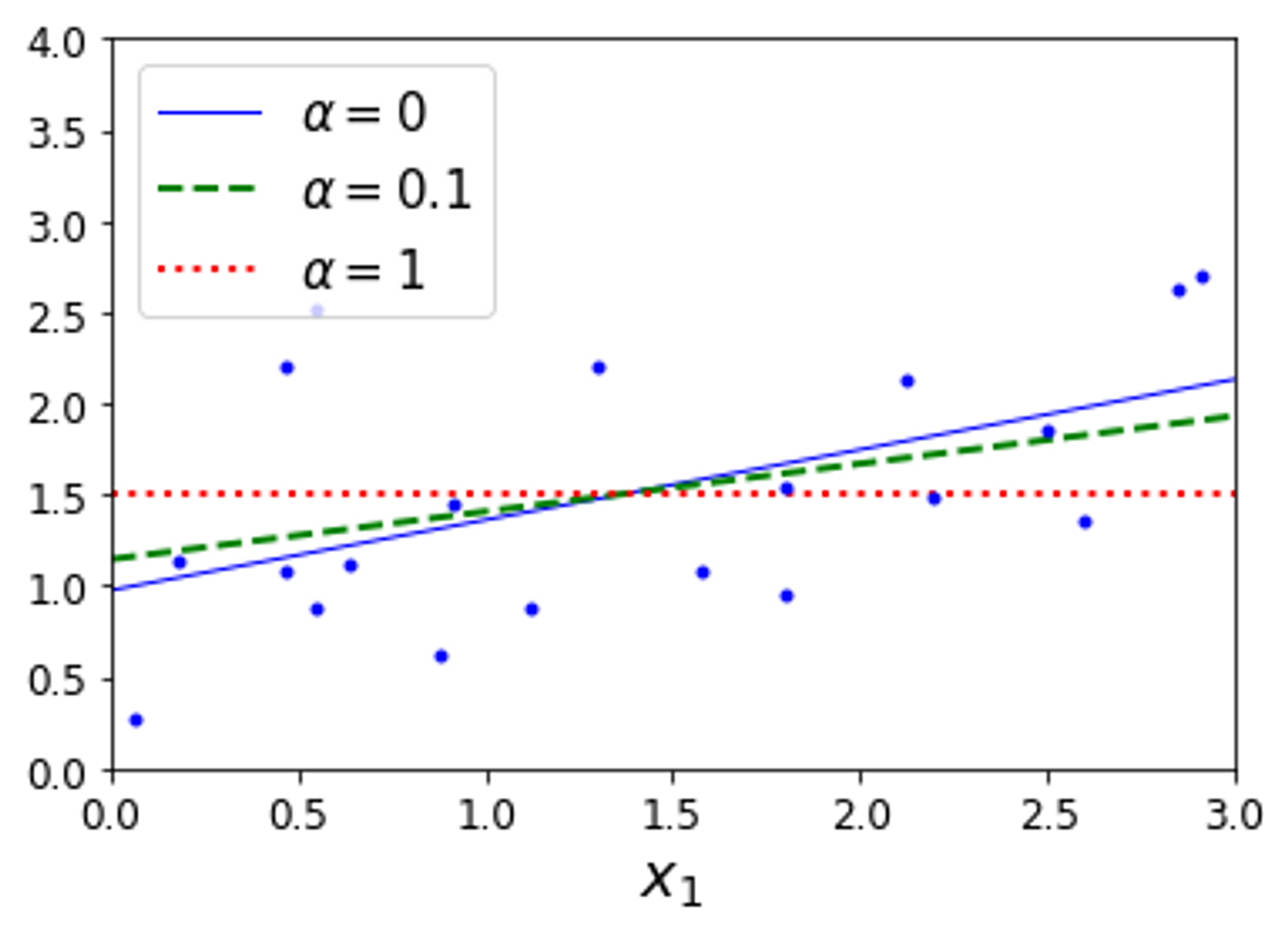
→ 라쏘 규제를 사용한 선형 회귀
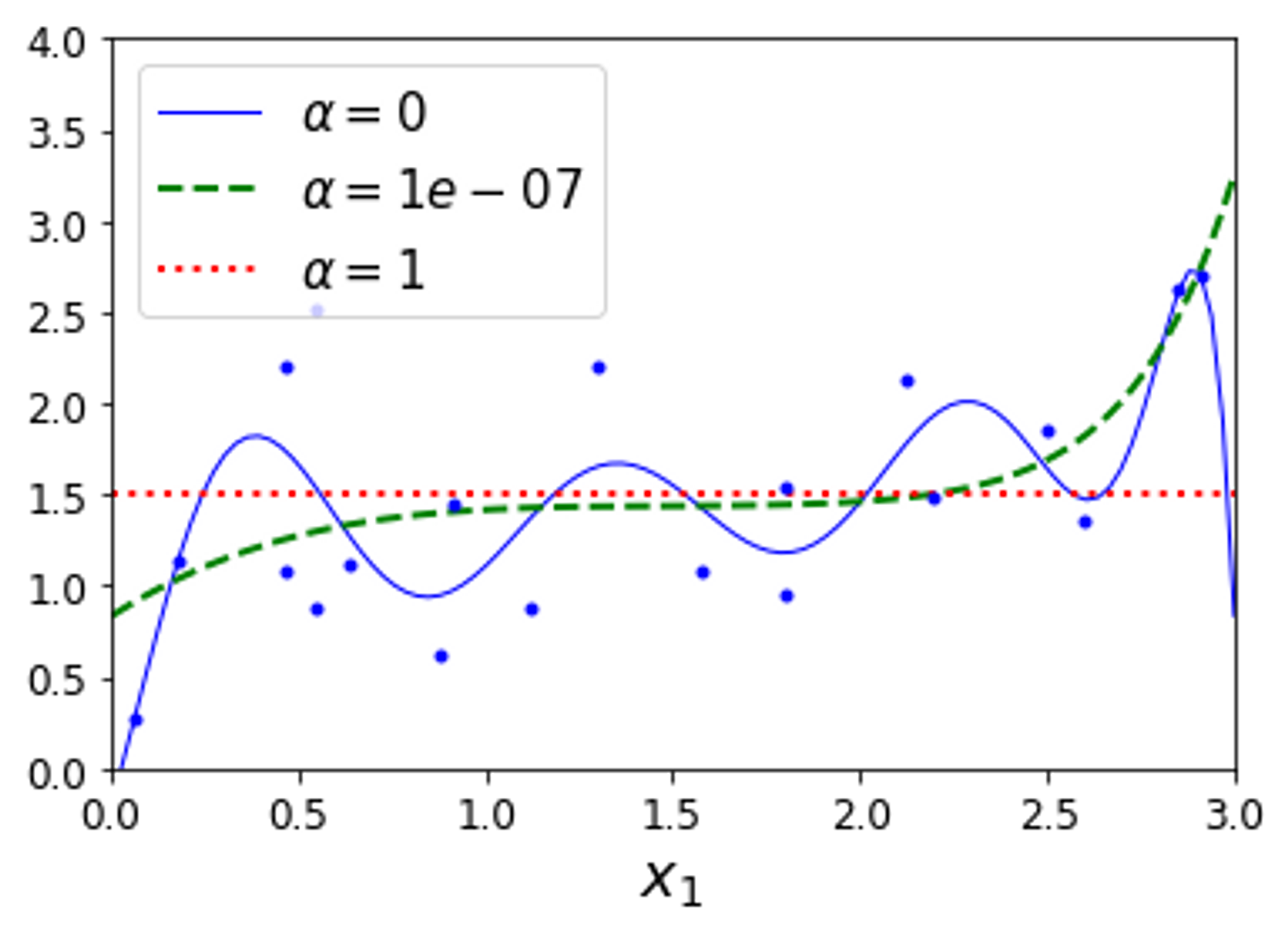
→ 라쏘 규제를 사용한 다항 회귀
a = 1e-07 의 그래프는 3차 방정식 처럼 보인다.
- ✅ 라쏘 회귀는 자동으로 특성 선택을 하고 희소 모델을 만든다.
🤔 라쏘 회귀(Lasso Regression) 과 릿지 회귀(Ridge Regression) 의 차이점을 알아보자 ‼️
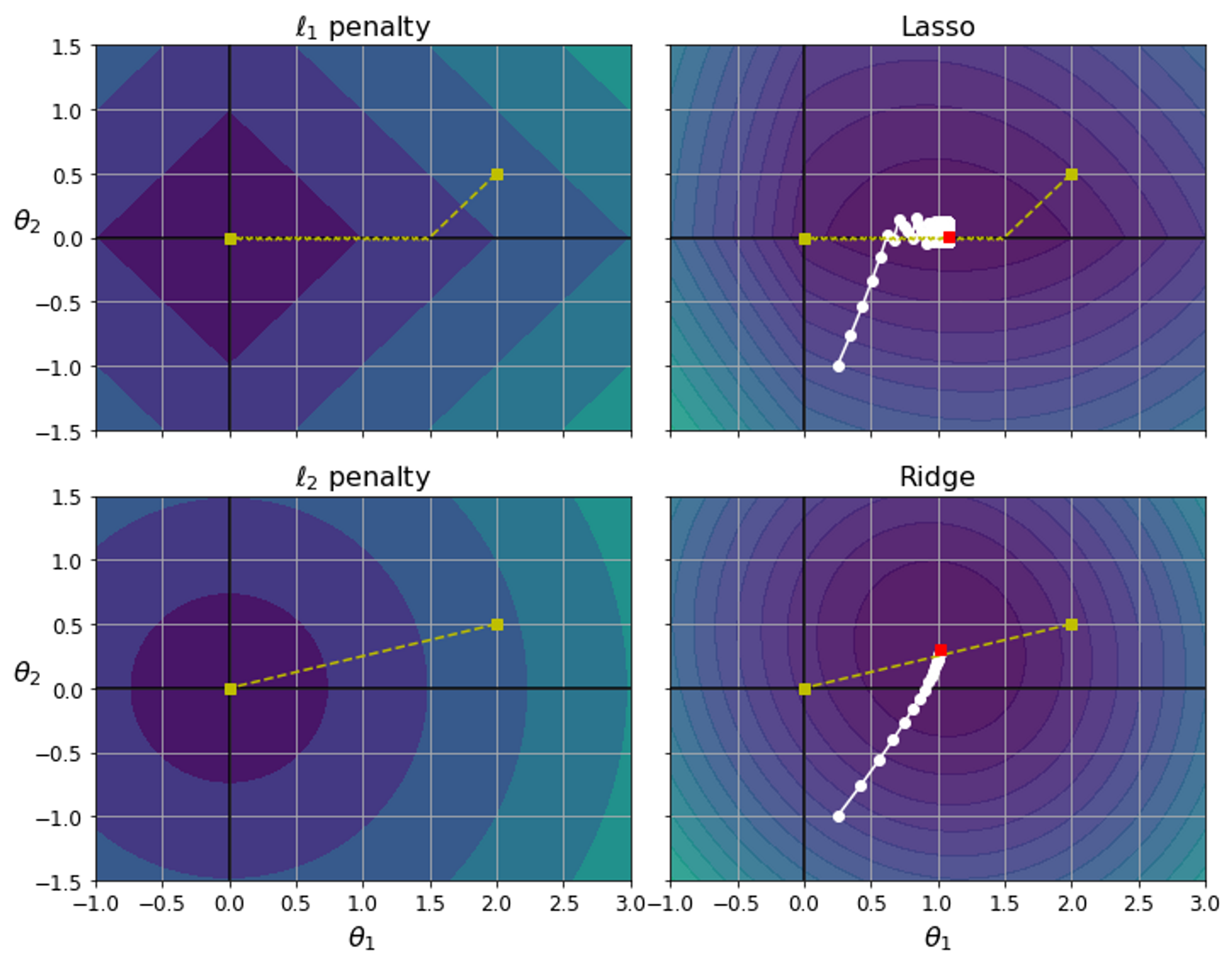
🟨 라쏘 회귀 : 왼쪽 위 그래프가 라쏘의 손실을 나타낸다 . 값에서 경사하강법을 실시하면 가 먼저 0에 도달한다. 오른쪽 위 그래프는 라쏘의 손실 함수를 나타낸다. 여기서도 으로 빠르게 줄어들고 그 다음 축을 따라 진동하며 전역 최적점에 도달한다.
🟨 릿지 회귀: 왼쪽 아래 그래프는 릿지의 손실을 나타낸다. 원점에 가까울수록 손실이 줄어드는 것을 확인할 수 있다. 오른쪽 아래 그래프는 릿지의 손실 함수를 나타낸다. 를 증가시킬수록 최적의 파라미터가 원점에 더 가까워진다. (진동이 없음)
✔️ 라쏘는 제약 조건이 절댓값 이기 때문에 마름모 꼴로 나타난다. 라쏘 회귀의 경우 최적값은 모서리 부분에서 나타날 확률이 릿지에 비해 높기 때문에 몇몇 유의미하지 않은 변수들에 대해 계수를 0에 가깝게 (또는 0) 으로 추정해 feature selection의 효과 를 가져온다. 라쏘는 파라미터의 크기에 관계 없이 같은 수준의 reularizaton 을 적용하기 때문에 작은 값의 파라미터를 0으로 만들어 해당 변수를 모델에서 삭제하고, 따라서 모델을 단순하게 만들어주고 해석을 용이하게 한다.
✔️ 하지만 릿지의 경우 어느정도 상관성을 가지는 변수들에 대해 pulling 이 되는 효과를 보여줘서 변수 선택 보다는 상관성이 있는 변수들에 대해 적절한 가중치 배분을 하게 된다. 따라서 릿지의 경우 PCA 와 관련성이 있다.
🟠 Ridge 와 Lasso
| Ridge | Lasso |
|---|---|
| L2 - norm | L1 - norm |
| 변수 선택 불가능 | 변수 선택 가능 |
| Closed form solution 존재 ( 미분으로 구함 ) | Closed form solution이 존재하지 않음(numerical optimization 이용) |
| 변수 간 상관관계가 높은 상황에서 좋은 예측 성능 | 변수 간 상관관계가 높을 때 Ridge에 비해 에측 성능이 떨어짐 |
| 크기가 큰 변수를 우선적으로 줄이는 경향이 있음 |
🟠 사이킷런을 이용한 Lasso 코드
from sklearn.linear_model import Lasso
lasso_reg = Lasso(alpha = 0.1)
lasso_reg.fit(X,y)
lasso_reg.predict([[1.5]])
💡 Lasso 대신 SGDRegressor(penalty = “l1”) 을 사용할 수도 있다.
참조

