[Java] BOJ 5639 이진검색트리 (Tree)

DAUN JO·2021년 8월 8일

algorithm boj tree

BOJ

목록 보기

8/35

BOJ 5639 S1 이진 검색 트리

트리
silver1

🔍 문제 설명

https://www.acmicpc.net/problem/5639

이진 검색 트리는 다음과 같은 세 가지 조건을 만족하는 이진 트리이다.

노드의 왼쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 작다.
노드의 오른쪽 서브트리에 있는 모든 노드의 키는 노드의 키보다 크다.
왼쪽, 오른쪽 서브트리도 이진 검색 트리이다.

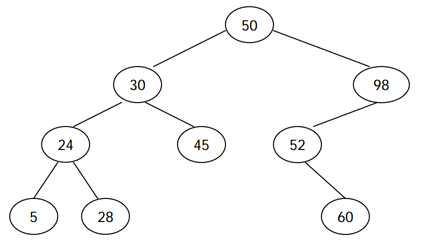
전위 순회 (루트-왼쪽-오른쪽)은 루트를 방문하고, 왼쪽 서브트리, 오른쪽 서브 트리를 순서대로 방문하면서 노드의 키를 출력한다. 후위 순회 (왼쪽-오른쪽-루트)는 왼쪽 서브트리, 오른쪽 서브트리, 루트 노드 순서대로 키를 출력한다. 예를 들어, 위의 이진 검색 트리의 전위 순회 결과는 50 30 24 5 28 45 98 52 60 이고, 후위 순회 결과는 5 28 24 45 30 60 52 98 50 이다.

이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.

✔ 입력

트리를 전위 순회한 결과가 주어진다. 노드에 들어있는 키의 값은 106보다 작은 양의 정수이다. 모든 값은 한 줄에 하나씩 주어지며, 노드의 수는 10,000개 이하이다. 같은 키를 가지는 노드는 없다.

✔ 출력

입력으로 주어진 이진 검색 트리를 후위 순회한 결과를 한 줄에 하나씩 출력한다.

💡 풀이

전위 순회 시 root->left->right의 순서로 노드를 방문한다.
후위 순회 시 left->right->root의 순서로 노드를 방문한다.

따라서 트리를 전위 순회한 결과를, 후위 순회한 결과로 바꾸는 과정은 다음과 같다.

먼저, 트리 전위 순회 결과를 바탕으로 root부터 출발하여 left, right를 구분한다.
이 때, left는 root보다 작은 노드들이고, right는 root보다 큰 노드들이다.

int root = preTree.get(start);

int right = start+1;
for(int i = start+1 ; i <= end ; i++) {
	if(root < preTree.get(i)) { //right를 찾는다.
		right = i;
		break;
	}
}

구분한 left, right를 바탕으로 또 다시 1번 과정을 반복한다.

getPostOrderTree(start+1, right-1); //왼쪽 서브트리 
getPostOrderTree(right, end); //오른쪽 서브트리

루트를 방문한다.

💡 소스코드

package week23.BOJ_5639_S1_이진검색트리;

import java.io.BufferedReader;
import java.io.FileInputStream;
import java.io.InputStreamReader;
import java.util.ArrayList;

/**
 * 
 * 
 * ✨ Algorithm ✨
 * 
 * @Problem : BOJ 5639 이진검색트리
 * 이진 검색 트리를 전위 순회한 결과가 주어졌을 때, 이 트리를 후위 순회한 결과를 구하는 프로그램을 작성하시오.
 * 
 * @Author : Daun JO
 * @Date : 2021. 8. 8. 
 * 
 *
 */
public class Main_BOJ_5639_S1_이진검색트리 {
	

	static ArrayList<Integer> preTree;
	static ArrayList<Integer> postTree;
	static int N;
	public static void main(String[] args) throws Exception {
		
		//System.setIn(new FileInputStream("5639input.txt"));
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		preTree = new ArrayList<>();

		//트리를 전위 순회한 결과가 주어진다.
		 while(true) {
			 String input = br.readLine();
			 if(input == null ) {
				 break;
			 }
			 preTree.add(Integer.parseInt(input));
		}

		//전위순회 : root->left->right
		//후위순회 : left->right->root
		
		//left는 root보다 작고, right는 root보다 크다
		
		N = preTree.size();
		getPostOrderTree(0, N-1);
		
	}
	private static void getPostOrderTree(int start, int end) {

		if(start>end) return; //기저조건

		int root = preTree.get(start);

		int right = start+1;
		for(int i = start+1 ; i <= end ; i++) {
			if(root < preTree.get(i)) { //right를 찾는다.
				right = i;
				break;
			}
		}
		
		getPostOrderTree(start+1, right-1); //왼쪽 서브트리 
		getPostOrderTree(right, end); //오른쪽 서브트리
		
		System.out.println(root); //루트 출력
	}
	
}