1. DSP Basic

홍종현·2022년 7월 5일

Audio

목록 보기

1/3

D&A Conference를 위해 음성 인식에 대해 스터디를 시작했다. 음성 인식에 대해 아는 지식이 별로 없어 기초부터 다지기로 했다.

현재 음성 인식은 인공지능이 기술이 더해져 빠른 기술 발전과 다양한 분야에 활용되고 있다. 소리 signal을 특정 data로 표현하며, 관련된 task를 해결할 수 있다.

1. Sound

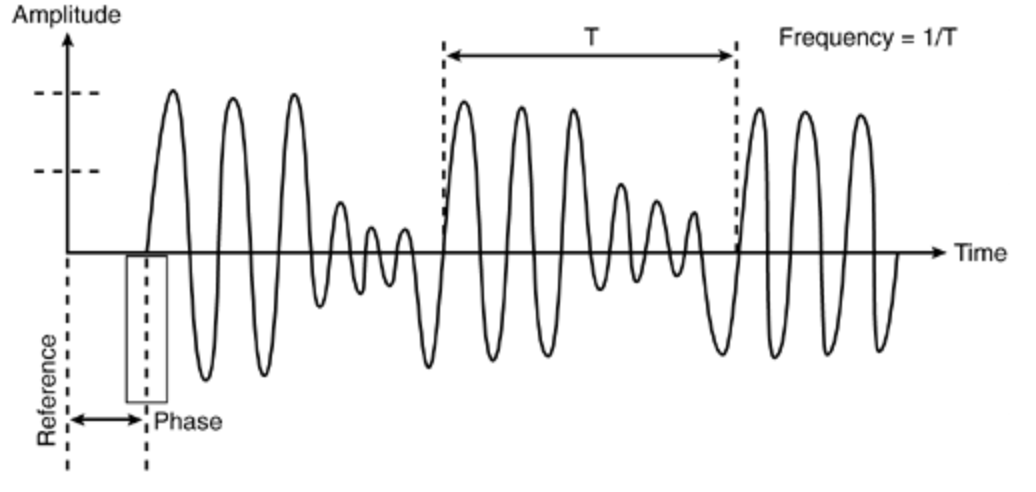
소리는 일반적으로 진동으로 인한 공기의 압축으로 생성된다. 압축이 어느정도냐에 따라 표현되는 것이 바로 파동, Wave이다. Wave는 진동하며 공간/매질을 전파해 나가는 현상을 의미한다. 이때 질량의 이동은 존재하지 않지만, 에너지의 운반은 존재한다. Wave에서 얻을 수 있는 물리량은 다음 3가지이다.

Amplitude: 진폭, wave의 진폭이 클수록 소리는 더 크게 남.
Frequency: 주파수, wave의 주파수는 소리의 높낮이를 결정.(고음은 진동수가 높고, 저음은 낮다.)
Phase: 위상, 소리의 맵시(바이올린의 도, 사람의 도, 피아노의 도는 다르다.)

2. Sampling

Sampling이란 아날로그 정보를 쪼개서 discrete한 digital 정보로 표현해야하는데, 특정 기준, t시간을 가지고 아날로그 정보를 쪼개서 대표값을 취하는것을 의미한다. Sampling 간격에 따라 amplitude가 달리지고 1초의 연속적인 신호를 몇개의 숫자들의 sequence로 표현하는것을 sampling rate $f_s$ 또는 Hz를 의미한다. 예를 들어, sample rate가 56.1KHz인 경우, 1초에 sample의 수가 약 56100개가 들어있는 것을 의미한다.

Sampling rate가 클수록 원본 data와 비슷한데, 그만큼 필요한 data의 양이 많아진다. 반대로, sampling rate가 작으면 Aliasing이라는 recording 품질을 저하 시키는 현상이 일어난다. Aliasing이란 digital signal 처리 과정에서 발생하는 noise로 연속적인 신호와 달라지는 일그러짐을 가리키는 현상이다.

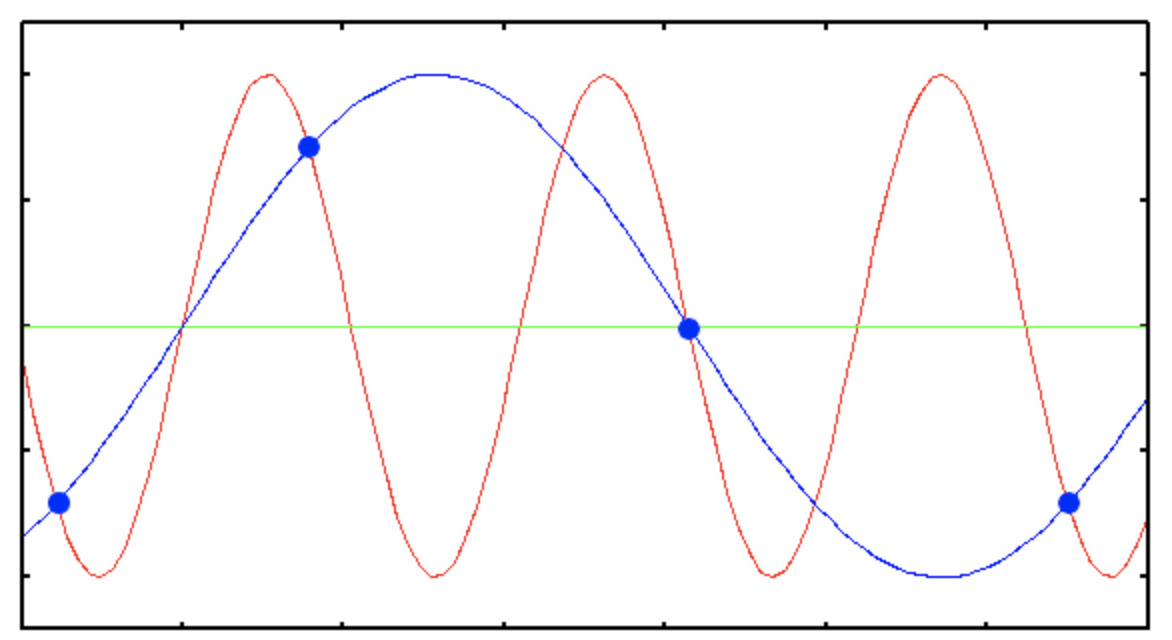
기존 붉은 선이 원래 신호인데 sampling rate가 낮으면 주파수가 낮은 파란색의 선 형태로 표현될 수 있다.

2.1 Sampling theorem

Nyquist 이론을 통해 sampling rate가 기존 신호에 존재하는 frequency의 2배 보다 크면 기존 digital signal을 표현할 수 있다고 한다.

f_s > 2f_m

f_s : sampling rate
f_m : maximum frequency

3. Resampling

Resampling은 sampling된 digital signal의 sampling rate를 조정하여 다시 sampling하는것으로 일반적으로 보간을 할 때는 low-pass filter를 사용한다.

4. Quantization & Normalization

4.1 Quantization

Quantization은 digital signal을 시간의 기준이 아니라 실제 amplitude의 real valued를 기준으로 signal 값을 조절하는것을 말한다. Amplitude를 이산적인 구간으로 나누고 signal data의 amplitude를 반올림하고 bit로 나타낸다. 비트 수가 커질수록 기존 digital signal의 정보 손실을 줄일 수 있지만, memory를 많이 잡아먹는다는 단점을 가지고 있다.

B bit의 Quantization : $-2^{B-1} ~ 2^{B-1}-1$

4.2 Normalization

Bit 값들을 normalization -1.0 ~ 1.0 size로 amplitude를 설정하고 보통 최댓값을 나눠주는 방법으로 scaling해준다.

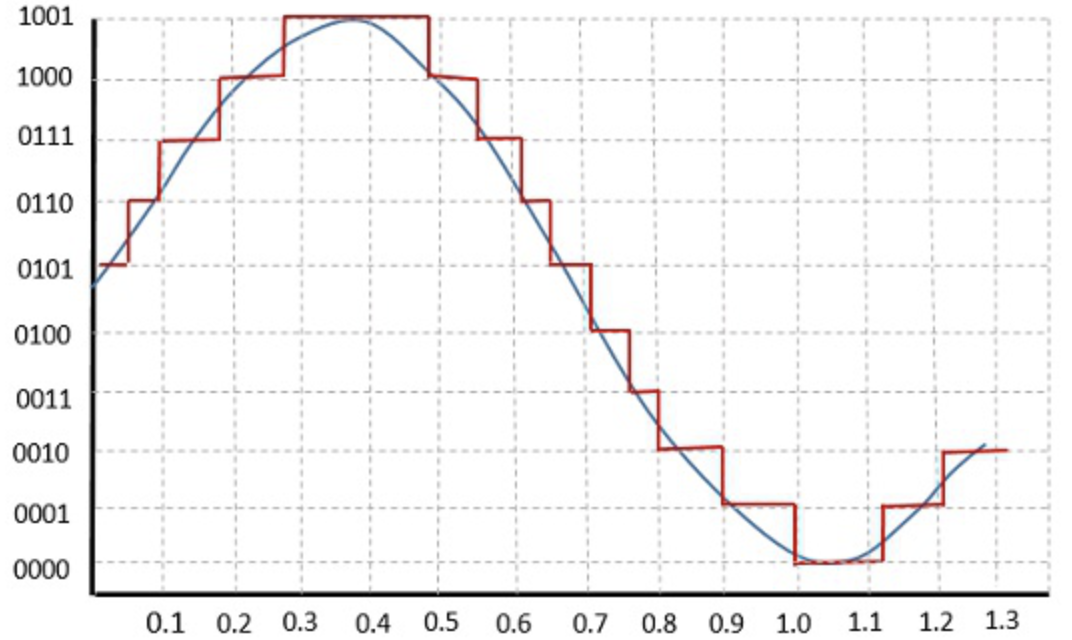
Quantization을 통해 light한 signal을 만들 수 있지만 음질은 다소 떨어질 수 있다.

4. mu-law encoding

사람의 귀는 소리는 작은소리의 차이는 잘 캐치할 수 있지만, 소리가 클수록 그 차이는 잘잡아내지 못한다. 1000Hz 이상에서는 주파수와 피치를 인식할 때, log형태를 띄고 100배정도 차이가 나야 2배정도 차이를 느낄 수 있다. 이러한 특성을 이용하여 wave값을 표현할 때, 작은 값에는 높은 분별력(high resolution)을 높은 값에는 낮은 분별력(low resolution)을 갖도록 한다.

5. Sound Representation

위의 방법들로 sampling된 discrete한 data를 표현하는 방법으로는 두가지가 존재한다.

Time-domain Representation : 시간의 흐름에 따라, 공기의 파동의 크기로 보는 방법
Time-Frequency Representation : 시간에 따라서 frequency의 변화로 보는 방법

5.1 Time domain - Waveform

Waveform의 경우에는 audio의 자연적인 표현으로 시간이 x축으로, amplitude가 y축으로 표현된다.

5.1.1 Sinusoid(정현파)

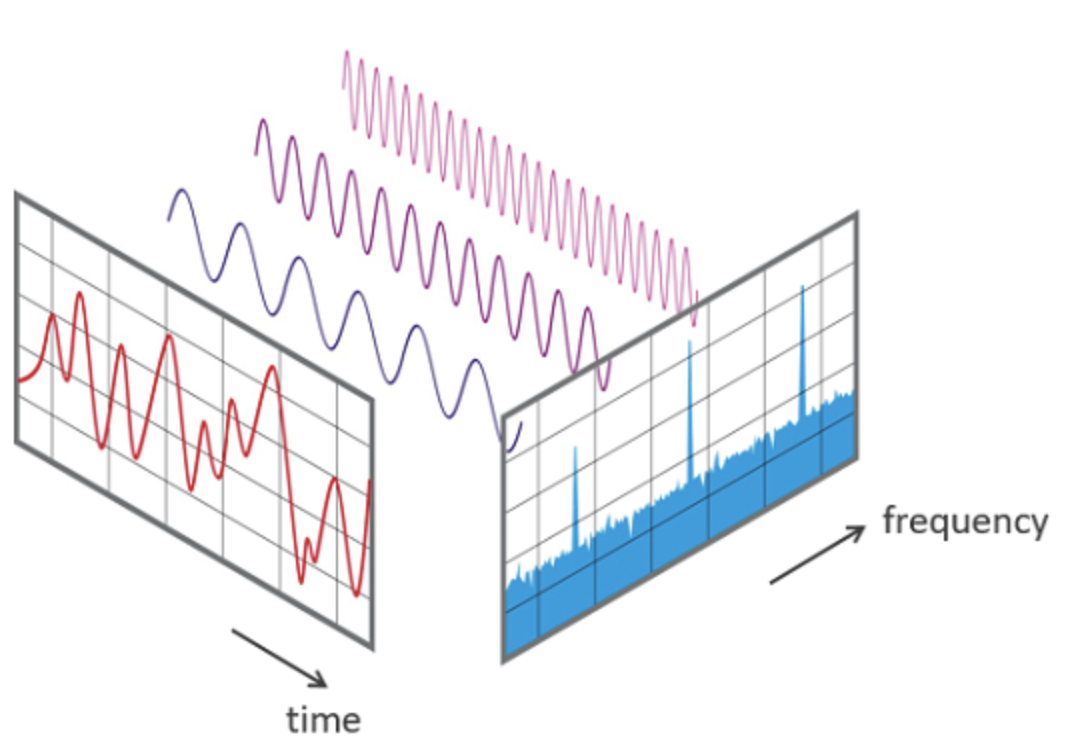
모든 digital signal은 frequency, magnitude, phase가 다른 sinusolida signal의 조합으로 나타낼 수 있다. 정현파는 주기신호를 의미하며 다음과 같이 나타낼 수 있다.

V = V_msin(2\pi ft + \theta)

$V_m$ : 크기
$sin$ : 파형
$2\pi ft$ : 주파수
$\theta$ : 위상

5.1.2 Fourier Transform

푸리에 변환은 임이의 digital signal을 다양한 주파수를 갖는 주기 함수(복수 지수함수)들의 조합으로 분해하여 표현하는것을 의미한다. 그리고 각 주기함수의 진폭을 구하는 과정을 퓨리에 변환이라고 한다.

일반적으로 푸리에 변환의 식은 다음과 같다.

F(u) = \int^{\infin}_{-\infin}f(x)e^{-j2\pi ux}dx

여기서 $j$ 는 $\sqrt{-1}$ 로 허수, $f(x)$ 는 입력 signal, $e^{-j2\pi ux}$ 는 주파수가 $u$ 인 주기함수 성분, $F(u)$ 는 해당 주기함수 성분의 계수를 나타낸다. 이 식을 직관적으로 해석하면 입력 신호 $f(x)$ 가 $e^{-j2\pi ux}$ 의 합으로 분해된다고 볼 수 있다. (적분은 합의 의미를 가지므로.) 그리고 $F(u)$ 는 해당 주기함수의 amplitude라고 해석할 수 있다.

이때, $e^{-j2\pi ux}$ 를 이해하려면 오일러 공식이 필요하다.

e^{j\theta} = cos\theta + jsin\theta

오일러 공식은 복소지수함수를 삼각함수로 변환하게 한다. 오일러 공식을 이용하면 $e^{-j2\pi ux}$ 는 실수부가 $cos(2\pi ux)$ 이고 허수부가 $sin(2\pi ux)$ 인것을 알 수 있다.

e^{-j2\pi ux} = cos(2\pi ux) + jsin(2\pi ux)

위의 식으로 푸리에 변환은 입력 신호와 상관없이 모두 cos, sin 주기 함수의 합으로 나타낼 수 있다.

5.1.2 Discrete Fourier Transform

Sampling된 data는 시간의 간격과 소리의 amplitude가 모두discrete한 data이다. 그러므로 위의 푸리에 변환 식을 discrete하게 바꿔줘야한다. 연속적인 신호 N개를 sampling한 이산적인 signal에서는 다음과 같이 푸리에 급수로 표현한다.

X_k = X(k\frac{2\pi}{N}) = \sum_{n=0}^{N-1}x[n] * e(-jk\frac{2\pi}{N}n)

$2\pi$ 로 반복되는 주기 함수에서 $k*\frac{2\pi}{N}$ 로 함수값을 이산적으로 만들어준다. 주기 함수를 자르는 간격은 $\frac{2\pi}{N}$ 으로 sampling과는 전혀 다르다. 이때 잘라진 함수 값을 $X(k\frac{2\pi}{N})$ 으로 나타낼 수 있다. 주기 함수를 일정한 간격으로 잘라서 나온 값이므로 이산적이라고 볼 수 있다.

5.1.3 Fast Fourier Transformation(FFT)

FFT는 빠른 푸리에 변환으로 DFT 구현을 위한 최적화된 알고리즘이다. DFT는 계산시간이 너무 오래 걸리기 때문에, sampling 된 신호의 전부를 변환시키는것이 아닌 필요한 신호만을 골라 최소화하여 푸리에 변환을 진행할 수 있다.

5.1.4 Short-Time Fourier Transform(STFT)

먼저 spectrogram과 spectrum의 차이를 알아보자. Spectrogram과 spectrum의 차이는 시간 축의 유무이다. Spectrum은 시간 축이 존재하지 않아 특정 시간의 snapshot을 찍어 소리를 나타낸것이고 spectrogram은 시간에 따른 소리의 변화를 나타낸것이다.

DFT는 시간에 흐름에 따라 신호의 주파가 변했을 때, 특정 시간대에 주파수가 변하는지 모른다. 그래서 시간의 길이를 나눠서 푸리에 변환을 해주는 STFT를 이용하면 시간에 따라 frequency값이 달리지는 것을 확인할 수 있다. STFT의 식은 다음과 같다.

X(l,k) = \sum_{n=0}^{N-1}w(n) x(n+lH)exp^{\frac{-2\pi kn}{N}}

$N$ : FFT size로, window가 얼마나 많은 주파수로 나뉘어 지는지

$Duration$ : sampling rate로 window를 나눈 값

$w(n)$ : window function

$n$ : window size, window function에 들어가는 sample의 양

$H$ : Hop size, window가 겹치는 사이즈로 보통 끊기지 않기 위해 1/4를 겹치게 함 (음성처리신호에서 frame 생성시 overlap을 하는 이유)

이렇게 계산된 STFT의 결과는 window size에 따른 frequency별 amplitude를 반환한다.

5.1.5 Window Function

Windowing이란 각각의 frame에서 함수를 적용해 경계를 smoothing하는 기법이다. Window function의 기능은 다음과 같다.

Main-lobe의 width를 제어
Side-lobe의 level trade-off를 제어
깁스 현상 방지(discrete한 wave가 푸리에 변환되었을 때, 나타나는 불일치 현상)

6. Spectogram

Spectogram은 소리나 파동을 시각화하여 파악하기 위한 도구로 waveform(파형)과 spectrum의 특징이 조합되어있다.

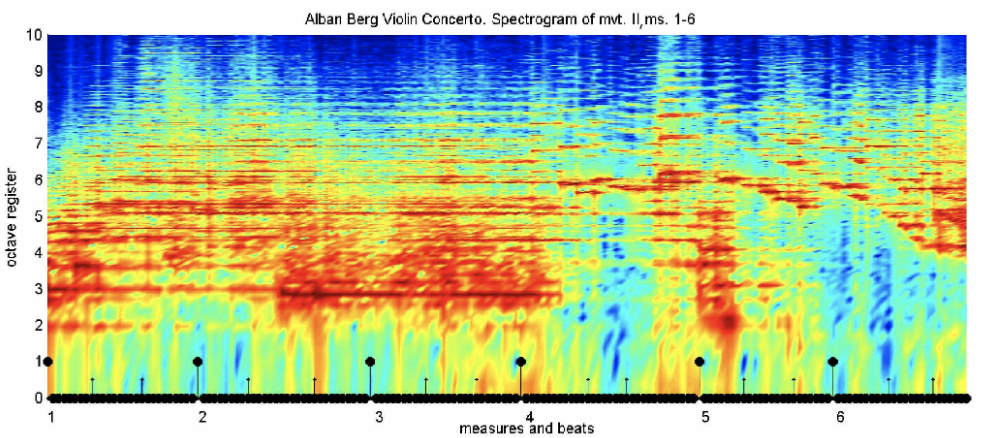
위 그림처럼, 시간 축과 주파수 축의 변화에 따라 진폭의 차이를 인쇄 농도나 색상의 차이로 표현한다.

일반적으로 process는 입력 신호가 window function을 통과해서 window size만큼 sampling 된 data를 discrete fourier transform을 거치게 된다. DFT를 거친 신호들은 frequency와 amplitude의 영역을 가지는 spectrum이 된다. 이후 이를 90도로 회전시켜 time domain으로 stacking할 수 있다.

또한, spectogram은 인간이 인접한 주파수를 잘 구분하지 못하기 때문에frequency scale에 대해서 scaling이 이루어진다. 인간의 인지기관은 categorical한 구분을 하기 때문에 주파수들의 binary 그룹을 생성하고 이들을 합하는 방식으로 진행된다. 인간은 보통 저주파에서 더 풍부한 정보를 얻을 수 있기 때문에, 주파수가 올라갈수록 filter의 폭이 높아지면서 고주파는 거의 고려를 하지 않는다.

6.1 Mel Scale

Mel spectrum은 주파수 단위를 다음 식에 따라 mel단위로 바꾼것을 의미합니다.

m = 2595log_{10}(1+\frac{f}{700})

일반적으로 mel-scaled bin을 FFT size보다 적게 만들고 mel-scaled의 사이즈를 줄이게되면, 정보가 압축되며 압축된 만큼 적은 noise가 생긴다. Data의 class별로 spectogram을 추출하여 평균 값을 보면, 어떤 frequency 영역대를 잡으면 좋을지 분별력이 생기게 되고, 그에 따라 size를 정할 수 있다.

6.2 Bark Scale

인간의 귀가 인식할 수 있는 주파수의 영역을 20Hz에서 200000Hz로 가정한다. 그러나 주파수에 대한 사람의 인식은 비선형적이기 때문에, 귀와 뇌의 가청대역을 24개의 대역으로 나눈것을 Bark라고 한다. Bark scale은 500Hz 이하에서는 100Hz의 대역폭을 가지며, 500Hz 이상에서는 각 대역의 중심 주파수의 20%에 해당하는 대역폭을 가지게 된다.

6.3 Log compression

Log compression은 다음과 같은 식으로 scaling을 진행한다.

10 * log10(\frac{S}{ref})

Spectogram을 데시벨 unit으로 전환해준다.

6.4 Discrete Cosine Transform(DCT)

DCT는 n개의 data를 n개의 cosine 함수의 합으로 표현하여 data의 양을 줄이는 방식을 의미한다. 저주파수에 에너지가 집중되고 고주파에서는 에너지가 감소하게 된다.

6.5 Mel-Frequency Cepstral Coefficients (MFCC)

Mel spectrum 혹은 log-mel spectrum은 태생적으로 feature 내 변수 간 상관관계가 존재한다. 그 이유는 주변 몇개의 Hz 기준 주파수 영역대 에너지를 한데 모아 보기 때문이다. 변수 간의 종속성을 해결하기 위해 log-mel spectrum에 inverse 푸리에 변환을 통해 변수 간 상관관계를 해소한 feature이다.

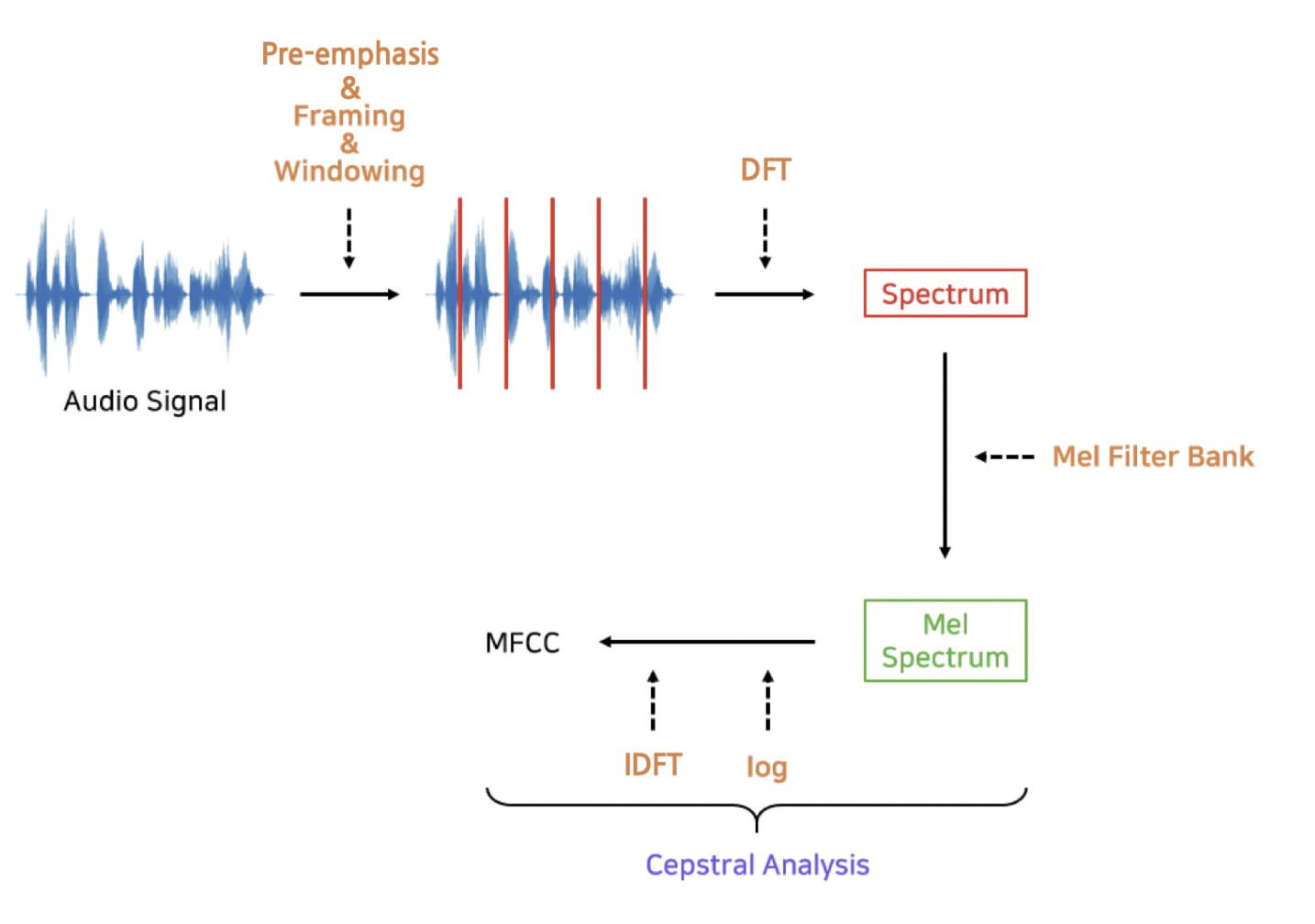
MFCC는 위 그림과 같이 waveform -> STFT -> Mel Filerbank -> log-mel spectrum를 거쳐 만들어진다. 이렇게 feature화 해주는 알고리즘이라고 볼 수 있는데 이것을 다시 말하면 음성 data를 벡터화 해주는 알고리즘이라고 볼 수 있다. 그러나 mel spectrum 혹은 log-mel spectrum 대비 MFCC는 구축과정에서 버리는 정보가 많다. 그러므로 최근 딥러닝 기반 model에서는 MFCC보다 mel spectrum 혹은 log-mel spectrum이 많이 쓰이는 추세이다.

홍종현

다음 포스트