Basic of Deep Learning Speech Recognition

홍종현·2022년 7월 19일

Audio

목록 보기

2/3

1. Audio Auto Tagging, Speech Recognition

1.1 Audio Auto Tagging

Audio Auto Tagging은 음성 신호가 들어왔을 때, 이벤트의 종류를 찾는 문제이다. 여러 소리를 동시에 인식하는것은 어려운 일이며 소리의 특성이 많이 다르거나 유사하면 인식하기 어렵다. 그러므로 특정 소리에 대해서 해당 오디오가 포함하는 여러 이벤트들을 tagging할 수 있는 Multi-label classification이 가능한 Audio auto tagging system이 필요하다. Waveform에서 얻어낸 spectral feature를 딥러닝 모델을 통해 feature를 얻고 이 feature를 이용하여 classifier를 학습하는 방식이다.

보통 Audio auto tagging을 평가할 때는 Average Precision, Rank-Average Precision metric이 많이 사용됩니다. 딥러닝 모델을 활용하여 mulit-label classification을 진행하면 각 label에 대한 점수 softmax 함수를 거쳐 합이 1인 vector로 나타나서 사용되는 metrics이다.

Audio auto tagging의 진행과정은 먼저 waveform 형태의 오디오를 RNN이나 CNN을 통해 feature extraction을 진행하고 classifier를 통해 학습한다.

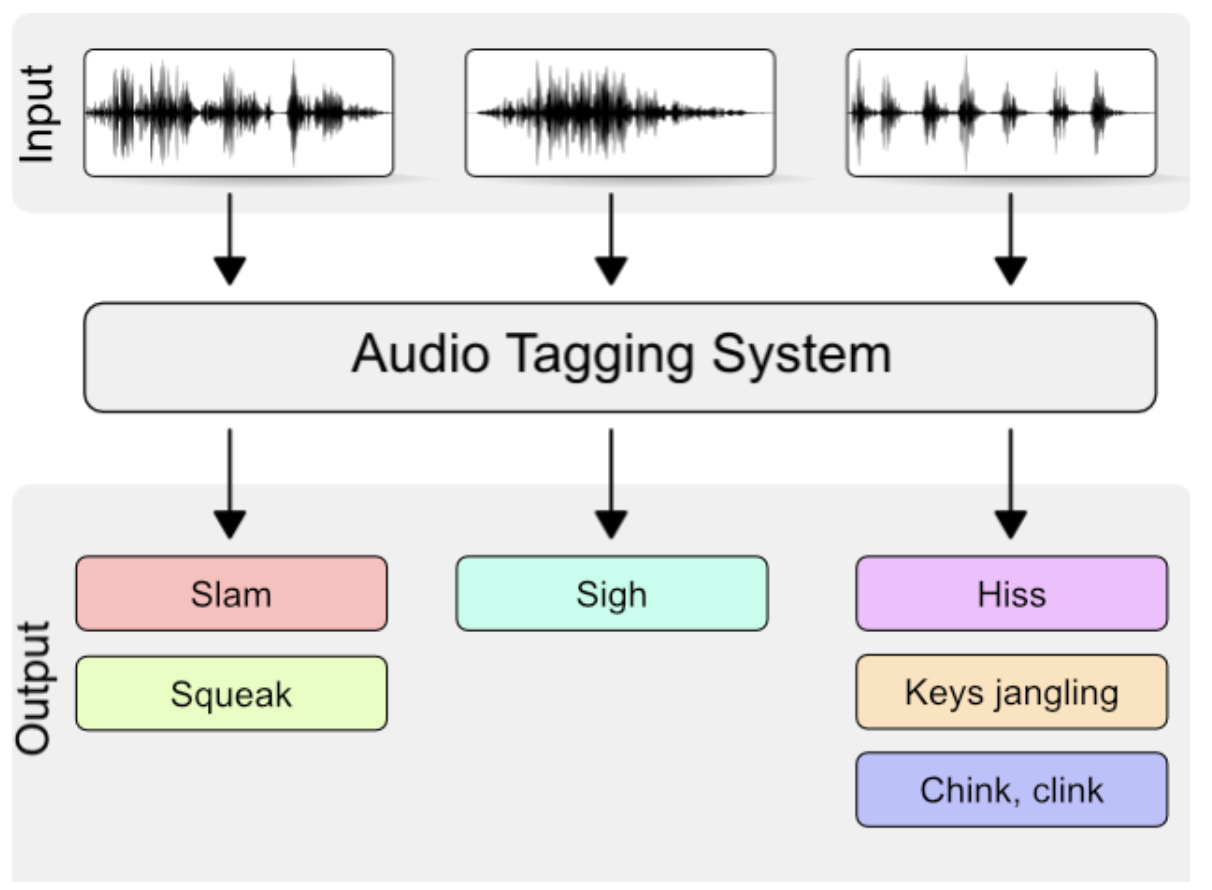
1.2 Speech Recognition (STT)

음성 인식이란 사람의 음성을 텍스트로 변환해주는 task를 의미한다. STT의 알고리즘은 음성 인식 및 입력 > 자연어처리 > 인식결과의 과정을 거치게 된다. STT의 음향 모델의 시작은HMM(Hidden Markov Model)이며 확률 통계 방식이다. 그리고 최근에는 Seq2Seq 방식의 RNN 기반으로 속도와 성능면에서 좋은 결과를 가져왔으며 또한 CTC(Connectionist Temporal Classification)라는 model로 입력 데이터와 레이블 사이의 alignment 정보 없이 학습이 가능하게 되었다.

2. CTC Loss (Connectionist Temporal Classification)

Speech Recognition task에서 우리는 dataset으로 audio clip과 transcript를 받게 된다. 하지만 그냥 이렇게 모델에 집어넣기에는 단어의 음소와 auido의 alignment를 알 수가 없다. 또한 사람들의 단어와 말하는 속도, 등 다양한 요소가 존재하기 때문에 단일한 rule로 정의하기는 쉽지 않다.

Input과 output 사이의 정확한 alignment가 labeling되어 있는 dataset은 필요없고 input이 들어왔을 때 output이 발생할 확률이 필요하다. CTC는 둘 사이의 가능한 모든 alignment의 가능성을 합하는 방식이다.

CTC 기법은 sequence를 분류하기 위해 모델 마지막 단에 loss를 통해 gradient를 업데이트하는 layer로 구분된다. CTC layer의 input으로는 output을 출력하게 되는 확률 vector로 RNN, transformer와 같은 sequence 출력을 가지는 모델에 CTC 기법을 적용할 수 있다.

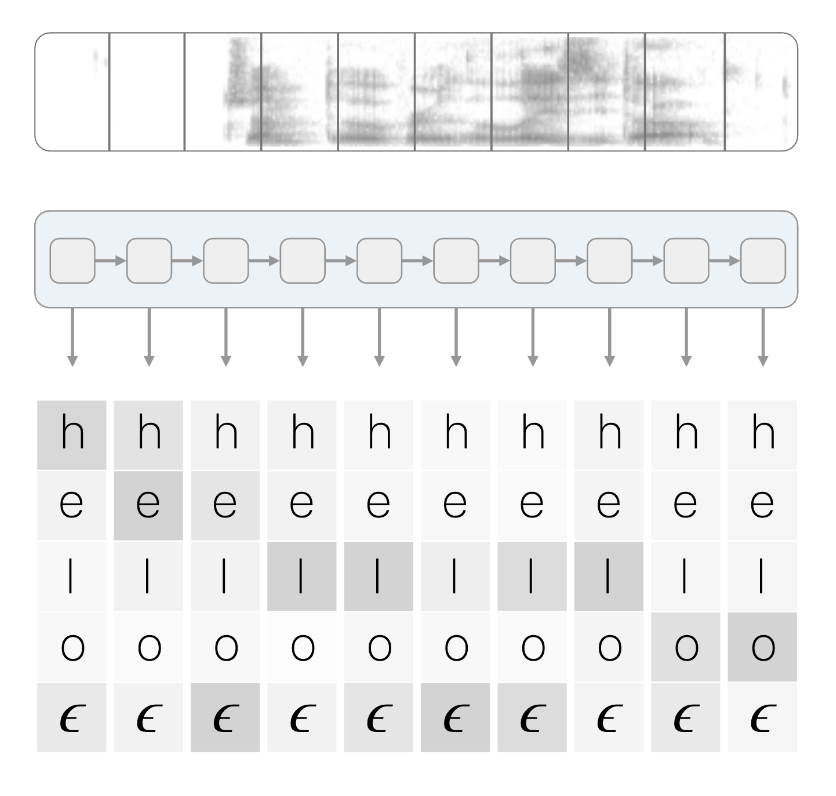
위의 그림에서 확인할 수 있듯이 CTC layer의 input에는 $\epsilon$ 이 추가되어있는것을 확인할 수 있다. 이것은 blank로 CTC에 들어가는 전체 음소수에 1을 더하여 총 dimension이 이루어진다.
CTC layer에서는 위의 그림과 같이 확률 vector의 sequence를 입력 받아 손실을 계산하고 그에 따른 gradient를 계산하는 방식으로, 여느 딥러닝 모델과 같이 역전파를 통해 이를 갱신한다.

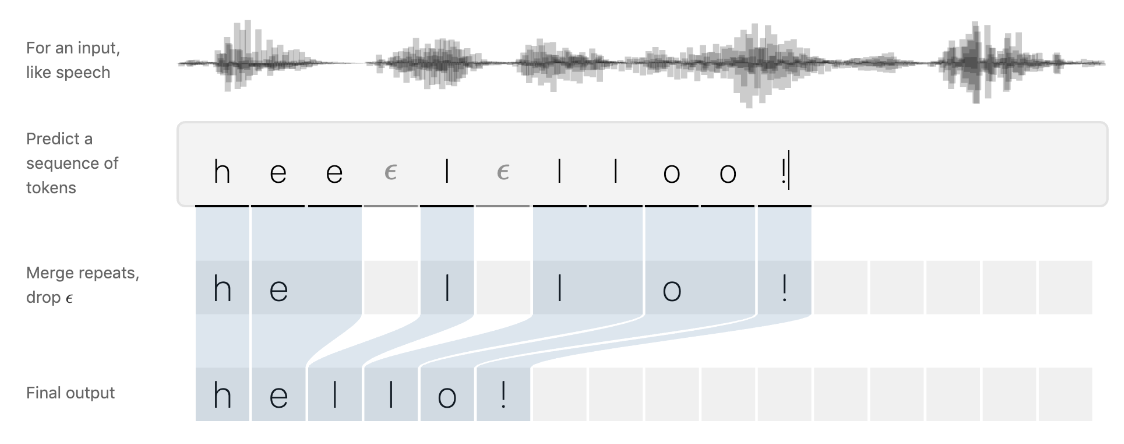
먼저 입력 프레임별 예측 결과를 decoding하여 반복되는 음소와 blank를 제거하는 후처리 과정을 거쳐 최종 output을 산출한다.

2.1 All Possible Paths

CTC기법에서는 label과 label 사이의 transition을 다음 3가지의 경우로만 한정한다.

selp-loop : 자기 자신을 반복
left-to-right : non-blank label을 순방향으로 하나씩 전이, 역방향은 허용하지 않음, 두개 이상 건너뛰는 것 역시 허용하지 않음
blank 관련 : blank에서 non-blank / non-blank에서 blank로 전이

Sequence가 h,e,l,l,o일 때, 위의 세가지 조건을 통해서 모든 경로를 고려하면 다음과 같다.

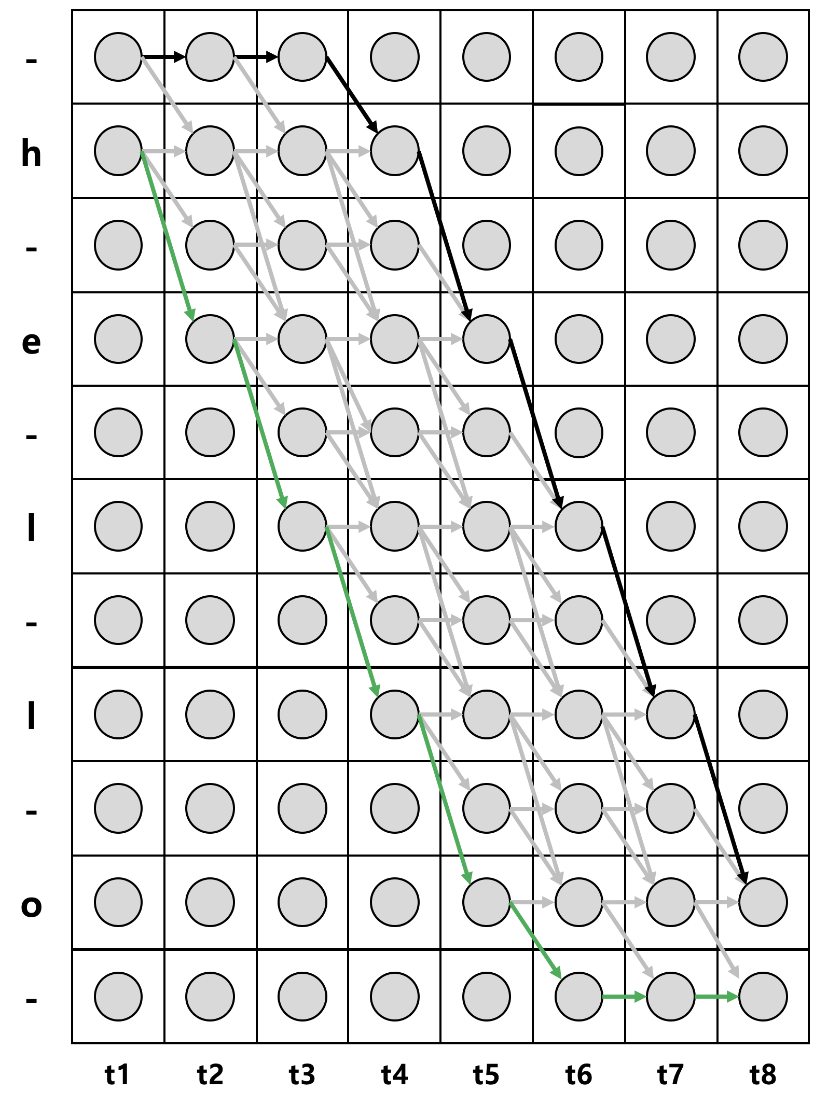
각 label의 시작과 끝에 blank를 추가하면 sequence의 길이는 2xsequence +1이 된다.

언어의 조음 규칙상 절대로 발음될 수 없는 일부 경로를 제거해서 그리면 다음과 같다.

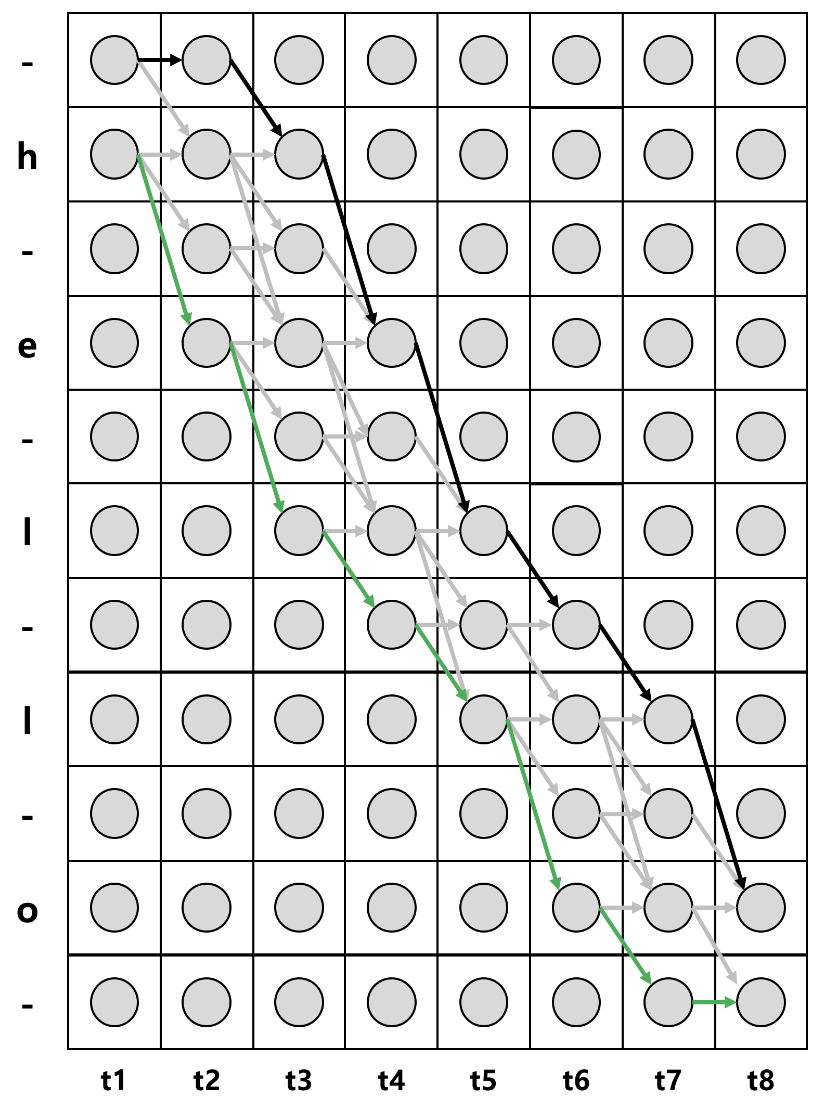
위 그림에서 x축은 각 time-step을 나타내고 y축은 음소(state)를 나타낸다. 각 세로 열은 각 시점에서의 확률 벡터로 원 하나는 개별 확률값을 의미한다. 예시로 2번째 행과 3번째 열에 존재하는 동그라미는 t가 3일 때, 상태가 h일 확률을 의미한다.

CTC 기법에서는 각 모든 상태가 조건부 독립이라고 가정한다. 즉 입력 음성 feature(input)에서만 label에 대한 확률 값(output)만 변하고 각 시점의 이후와 이전에는 어떠한 영향도 없다고 가정한다. 그래서 음성 input이 주어졌을 때, label이 나타날 확률의 곱으로 수식을 나타낼 수 있다.

p(\pi|x) = \Pi_{t=1}^Ty_{\pi_t}^t

$\pi$ : 경로
$x$ : 음성 input
$y_{\pi_t}^t$ : 경로(상태) $\pi$ 일 때, 확률 값

이것은 해당 레이블을 나타낸 확률 값으로 조건부 확률이다.

Input 음성 feature가 주어졌을 때, 전체 sequence가 나타날 확률은 모든 경로의 확률 $p(\pi|x)$ 합이다.

p(l|x) = \sum_{\pi \in B^{-1}(l)} p(\pi|x)

$l$ : 전체 sequence

여기서 $B$ 는 blank와 중복된 label을 제거하는 함수로 예를 들어, $B(hhhhel-llooo-) = B(hello)$ 라고 생각하면 된다. $B^{-1}(l)$ 은 blank와 중복된 레이블을 삭제한 $l$ 이 될 수 있는 모든 경로가 포함되어 있는 집합이다.

2.2 Foward Computation

앞에 두식에서 $p(l|x)$ 를 구하려면 모든 경로와 그에 대한 시점, 상태에 대한 확률을 계산해야한다. 즉, Sequence의 길이가 길어지거나 음소 개수가 많아지면 계산량이 급증하게 된다. CTC는 이를 방지하기 위해서 Hidden Markov Model과 같이 Forward와 Backward 알고리즘을 사용한다.

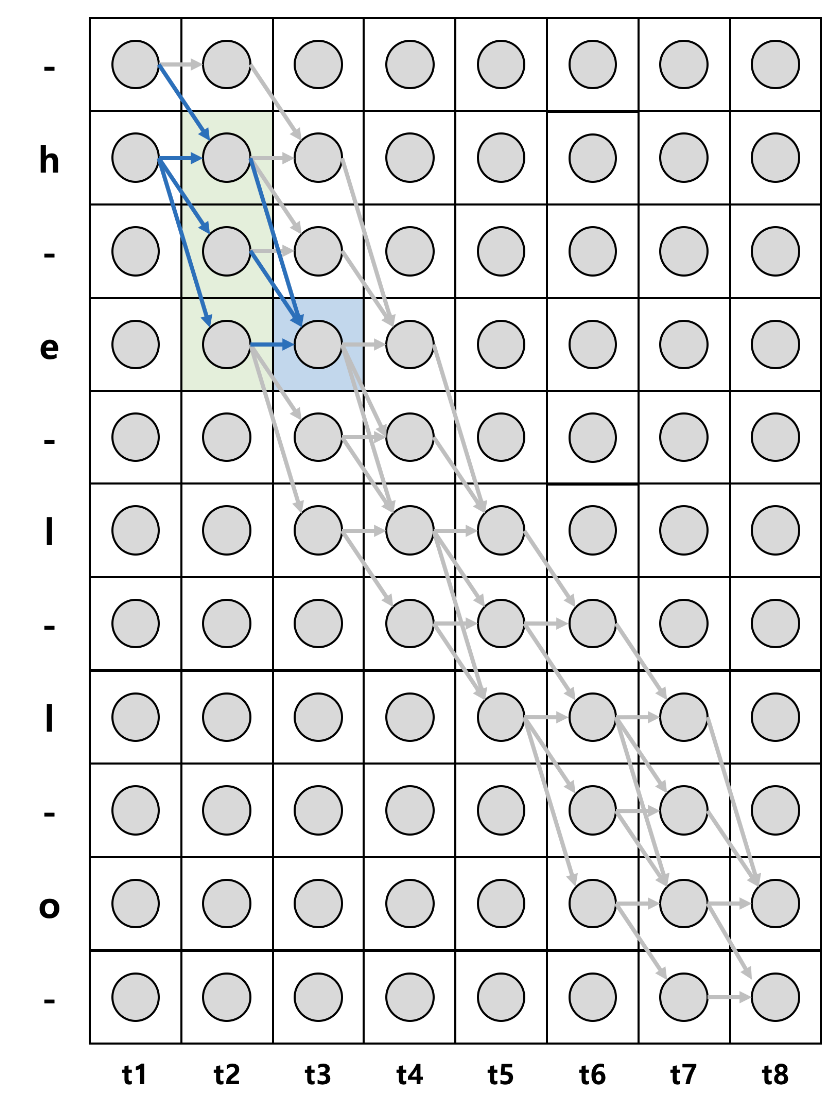
파란색 상자의 확률을 구해보자.
이를 $a_3(4)$ 라고 한다면 t=1시점에서 state는 1인 '- 또는 t=1 시점에서 state는 2인 'h'에서 시작하여 시간의 순서에 따라 경로가 이어진다. 파란색 상자는 결국 t=3시점에서 s=4 'e'가 나타날 확률을 구하는 것이다. t=3일 때, e가 나오려면 총 4가지 경우가 존재한다. (-he, hhe, h-e, hee)

여기서 만약 -he가 나타날 확률을 구하려면 조건부 독립을 가정했으므로 각 시점에서 해당 상태가 나타날 확률을 모두 곱해주면 된다. 나머지 hhe, h-e, hee도 같은 방식으로 구하게된다.

a_3(4) = p(-he|x) + p(hhe|x) + p(h-e|x) + p(hee|x)

y_{-}^1 * y_h^2 * y_e^3 + y_h^1 * y_h^2 * y_e^3 + y_h^1 * y^2_- * y_e^3 + y_h^1 * y_e^2 * y_e^3

전방확률을 계산한 식이고, 1 : $t$ 시점에서 label sequence가 1:s로 나타날 확률을 의미한다. 이러한 수식은 결국 대상까지의 경로인 $\pi$ 를 구하는것이다. t시점까지의 $\pi$ 에서 blank와 중복을 제거한 label의 결과는 label의 sequence와 일치해야한다. 위에서 언급한 예로 hhe, h-e, hhe, -he에서 중복된 레이블과 blank를 제거하면 모두 he로 동일하다.

결국 CTC는 입력 음성 sequence 가각에 대한 sequence label를 alignment해주는 역할을 한다고 볼 수 있다.

그리고 forward computation을 모두 계산할 경우, 계산량이 너무 복잡해지는데 이를 다이나믹 프로그래밍을 통해 개선할 수 있다. 이는 겹치는 부분을 저장해둬서 다시 사용하는 알고리즘으로 식을 통해서 확인하면 쉽다.

a_3(4) = p(-he|x) + p(hhe|x) + p(h-e|x) + p(hee|x)

= y_{-}^1 * y_h^2 * y_e^3 + y_h^1 * y_h^2 * y_e^3 + y_h^1 * y^2_- * y_e^3 + y_h^1 * y_e^2 * y_e^3

= {(y_-^1*y_h^2+y_h^1*y_h^2) + (y_h^1*y_-^2) + (y_h^1 * y_e^2)}y_e^3

= {a_2(2) + a_2(3) + a_2(4)}y_e^3

구하려는 시점 전까지, 이미 계산해놓은 $a_2(2), a_2(3), a_2(4)$ 을 재사용하면서 계산량을 줄일 수 있다.
이를 Forward Algorithm이라고 하는데 두가지 경우를 고려해야한다. 계산하려고 하는 시점에서의 label값이 blank이거나, 현재 상태와 그 직직전 상태가 일치할 경우, 그리고 그외의 경우를 구분해야한다.

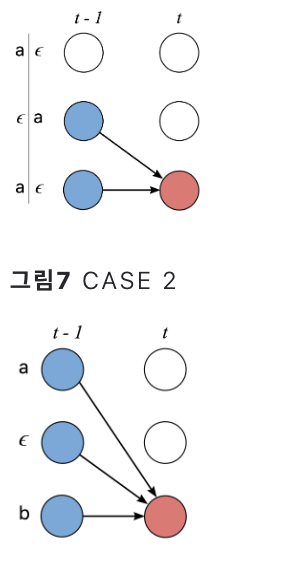
모든 고려사항을 종합하여 전방확률 계산을 나타낸 그림은 아래와 같다.

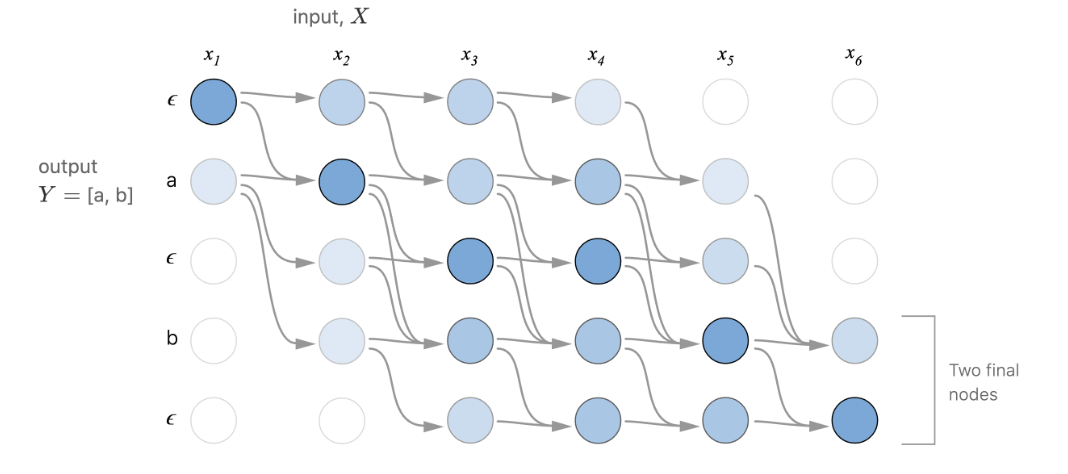
경로의 시작은 blank 혹은 첫번째 요소가 되고 두가지의 경우를 모두 고려하여 중간 경로를 설정한다. 이를 수식으로 표현하면 아래와 같다.

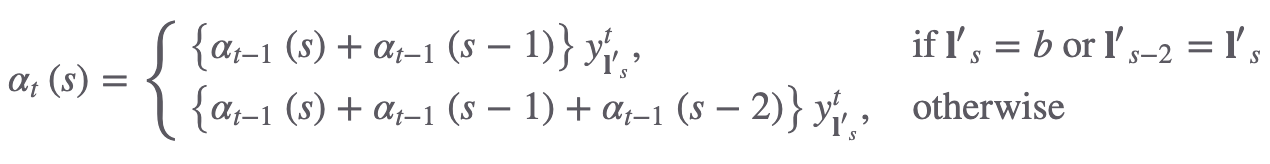
2.3 Backward Computation

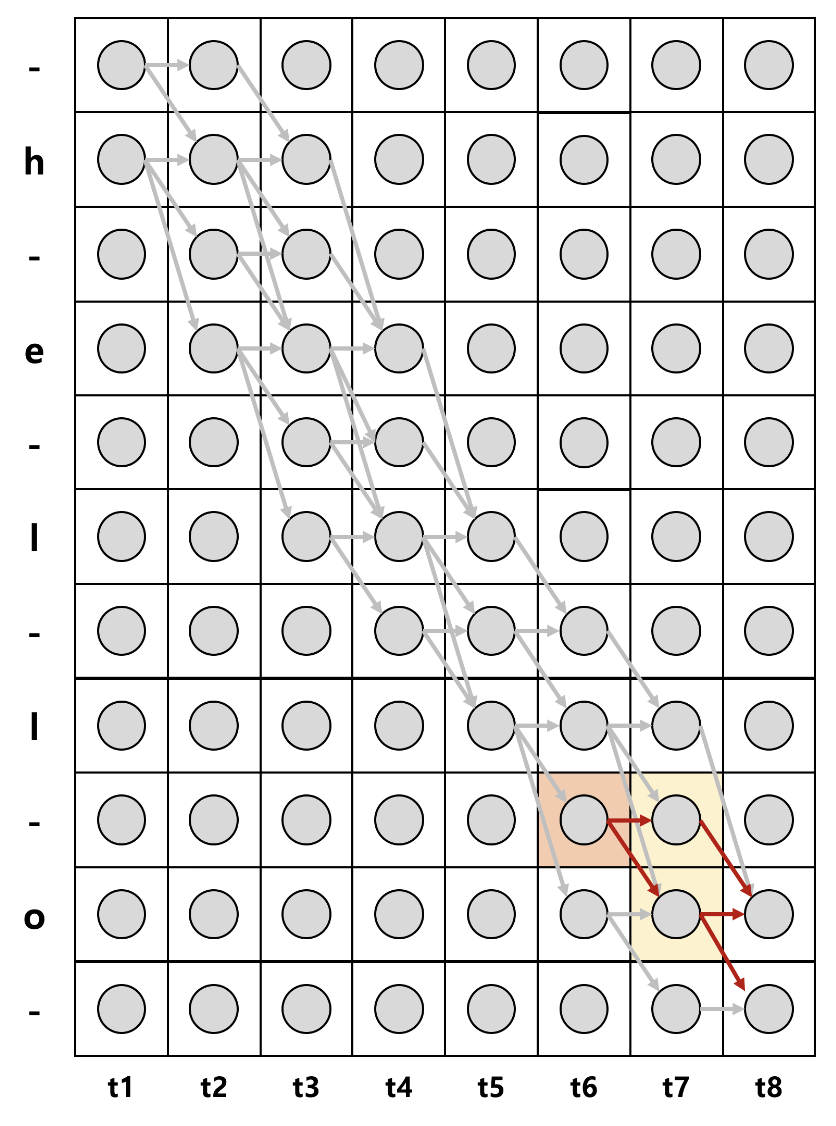
만약 오렌지색 칸, $B_6(9)$ 의 후방확률을 계산하면 다음과 같다. t = 8의 시점에서 s = 11의 상태 혹은 t = 8 시점에서 s = 10의 state의 상태에서 시작하여 시간의 역순으로 역전파를 진행한다. t = 6의 시점에서 s = 9의 상태 '-'가 나타날 확률을 의미한다. 우측 가장 하단 지점에서 t = 6 시점까지의 '-'가 나타나려면 두가지 경로가 존재하고 모든 경로를 고려하면 '--o', '-oo', '-o-'이다.

이를 수식으로 나타내면 아래와 같다.

B_6(9) = p(--o|x) + p(-oo|x) + p(-o-|x)

= y_-^6 * y_-^7 + y_-^6 * y_o^7 * y_o^8 + y_-^6 * y_o^7 * y_-^8

입력으로 들어온 음성 sequence의 길이가 $T$ 이고, target label의 sequence가 $l$ 이라고 한다면, t시점의 후방확률은 $t:T$ 시점에 걸쳐 label의 $s:l$ 일 확률을 나타낸다. 후방확률에도 두가지 조건이 존재한다.

t:T 시점까지의 $\pi$ 에서 blank와 중복 레이블을 제거한 결과가 s:|l|까지의 target label sequence와 일치해야함.
$\pi$ 는 개별 요소 state로 각각 N개의 범주를 가지며 시퀀스의 전체 length는 T이다.

Forward 계산과 같이 다이나믹 프로그래밍을 통해 계산량을 줄일 수 있다. 그저 방향만 달라졌다고 생각하면 되는거 같다.

2.4 Complete Path Calculation

정방향, 역방향 경로에 대한 확률을 순차적으로 계산하여 구했다면, 이번에는 특정 시점, 특정 상태를 지나는 경로에 대한 등장 확률을 구해보자. 이는 앞서 구한 전방 확률과 후방 확률을 통해 간단하게 계산할 수 있다.

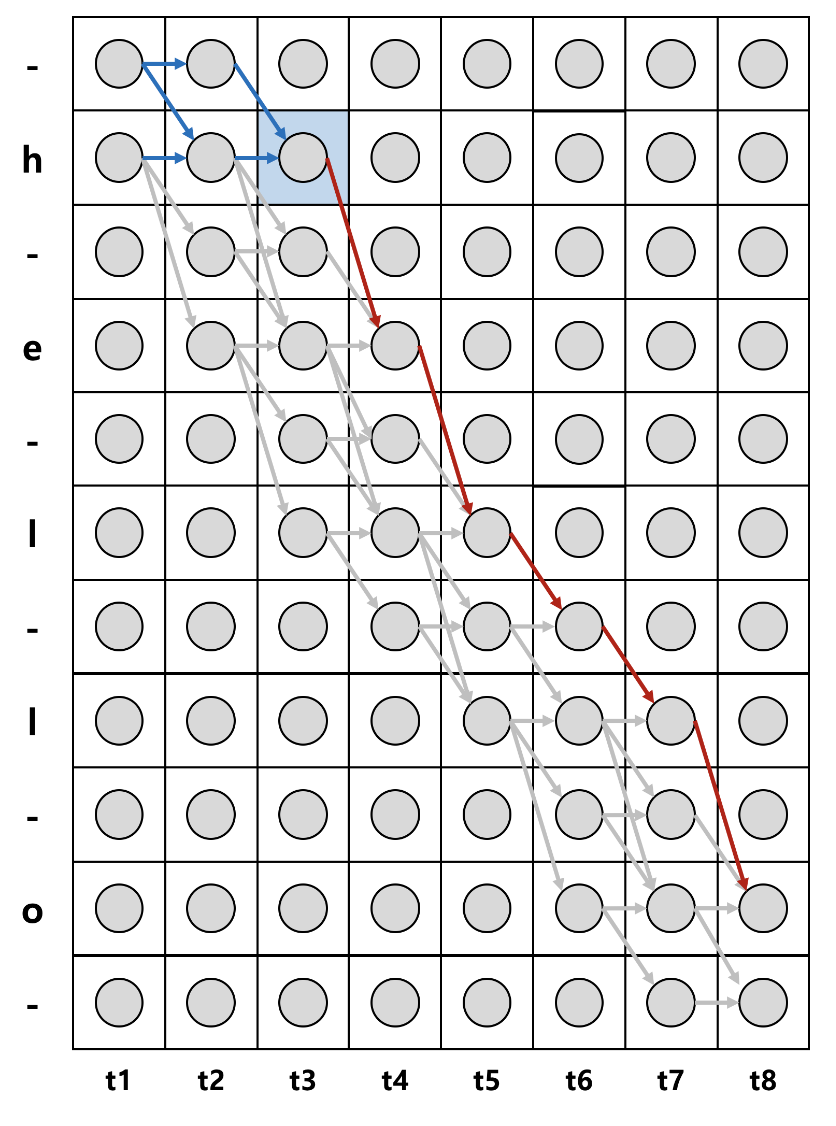
위 그림에서 파란색 칸은 t=3시점에서 state가 'h', s=2인 모든 경로에 대한 확률을 구해보자. 해당 경로는 '--hel-lo', '-hhel-lo', 'hhhel-lo' 3가지가 존재한다.

3가지 경로에 대한 확률은 모든 시점과 상태에 대해 전부 계산하면 구할 수 있지만, 전방 확률과 후방 확률을 활용하여 쉽게 구할 수 있다. 먼저 전방 확률과 후방 확률을 먼저 구해보자

a_3(2) = p(--h|x) + p(-hh|x) + p(hhh|x)

= y_-^1 * y_-^2 * y_h^3 + y_-^1 * y_h^2 * y_h^3 + y_h^1 * y_h^2 * y_h^3

B_3(2) = p(hel-lo|x)

= y_h^3 * y_e^4 * y_l^5 * y_-^6 * y_l^7* y_o^8

전방 확률과 후방 확률의 곱은 --hel-lo, -hhel-lo, hhhel-lo 3가지 경로에 대한 확률을 더한 값에 $y_h^3$ 을 곱해진 형태임을 확인할 수 있다.

a_3(2) * B_3(2) = {p(--hel-lo|x) + p(-hhel-lo|x) + p(hhhel-lo|x)} y_h^3

2.5 Likelihood Computation

결국 우리가 찾고싶은것은 input sequence가 들어갔을 때, label sequence가 나타날 우도를 최대화하는 parameter를 찾는것이다. 우리가 가진 데이터의 입력과 출력의 길이는 다르기 때문에 cross-entropy를 사용할 수 없다.

우리는 이 우도를 위해서 gradient를 구해야하고 학습 parameter에 역전파를 하는것이 CTC 기법을 적용한 model의 학습방법이다. 보통 log-likelihood로 수행하게된다. $ln(x)$ 를 $x$ 로 미분하면 $\frac{1}{x}$ 이고 우도에 로그를 취하고 이를 합성 함수라고 하면 chain rules가 성립한다. t번째 시점 k번째 state에 대한 log-likelihood의 gradient는 아래와 같이 계산된다.