13. 일반최소제곱법과 QR 분할

오늘 강의에선 QR분해에 대해서 배웠다. QR분해를 왜 하는것일까?

예를 들어, $Ax = b$라는 식의 $x$를 구하기 위해서는 A의 역행렬을 각각 곱해주면 된다. 그러나 역행렬을 구하는것은 시간이 오래걸리고 수치의 안정성이 떨어진다고 하여 행렬을 직교화하는 QR분해를 사용한다.

Generalized Least Square

일반최소제곱법(GLS)는 보통 선형 회귀에서 모르는 parameter에 대해 추정하는데 사용된다고 한다. 가중치를 마치 확률처럼 생각한다.

Orthogonal Basis

Orthogonal vector들을 통해 basis vector를 구성하여 vector space로 span할 수 있다. 기본적으로 어떠한 행렬 $Q$가 있을 때, 다음과 같은 식이 성립라면 Othonormal matrix이다.

Q matrix examples

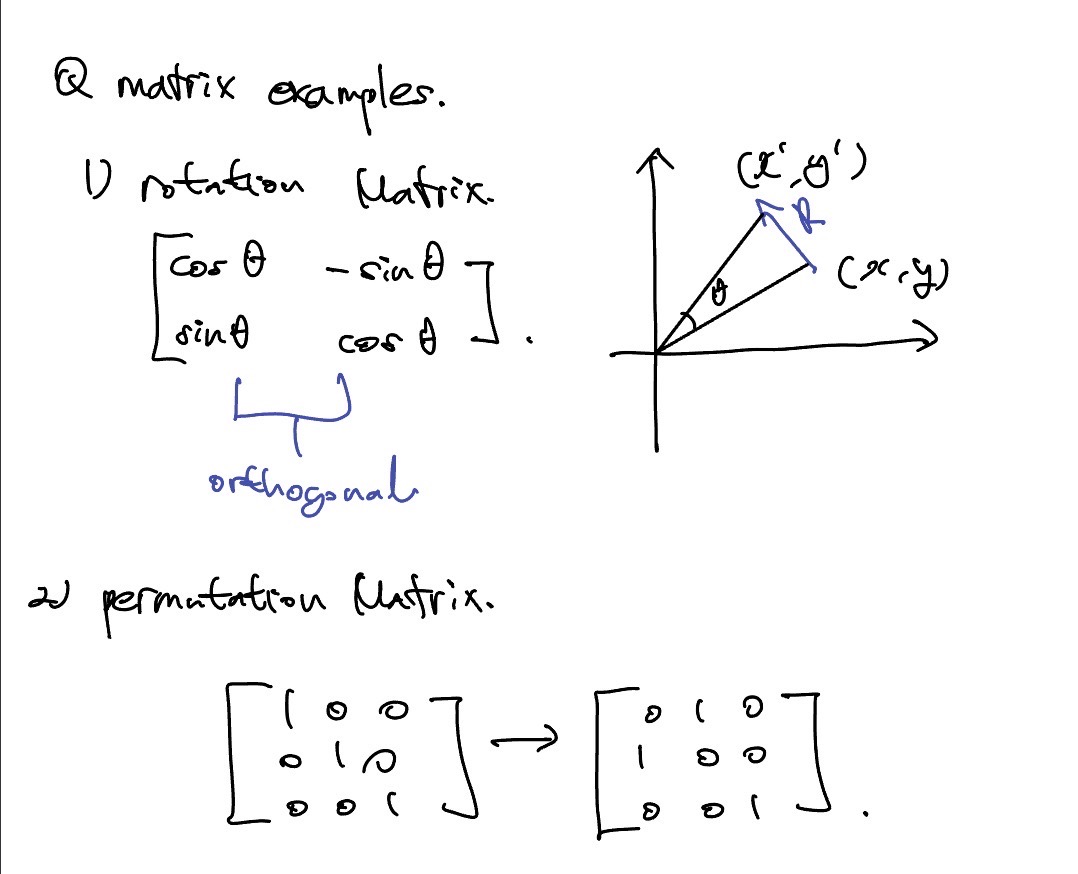
Rotation Matrix

$x = cos\theta$, $y = sin\theta$일 때, $(x,y)$가 특정 방향으로 $\theta$만큼 회전한 좌표점이 $(x^1,y^1)$이다.

Permutation Matrix

Identity matrix에서 순서를 바꾼 형태이다.

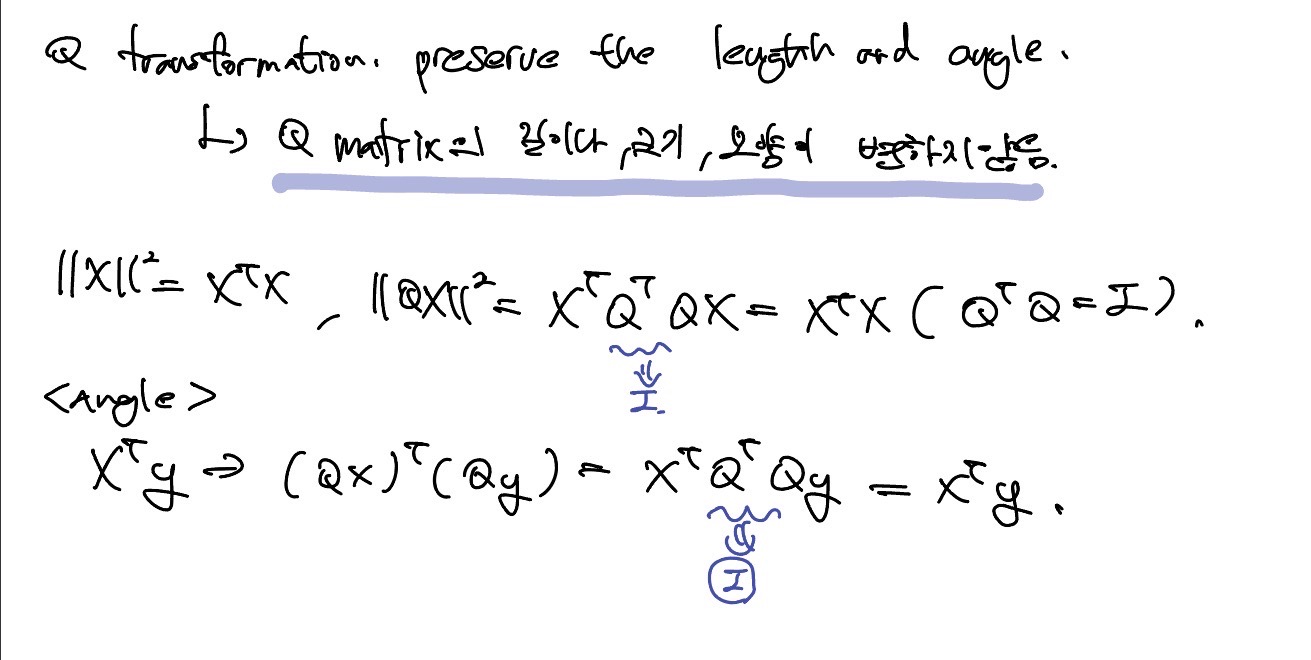
Q matrix는 길이나 크기 모양이 변하지 않는다. 각도는 내적을 통해서 증명이 가능하다.

n차원 space에서 선형 독립이면서 orthogonal한 vector들이 주어졌을 때, 다음과 같이 span할 수 있다.

$c_i$는 projection된 값으로 X라는 크기에 $q_i$라는 vector가 얼만큼 projection되어있는지 나타내는 값이다.

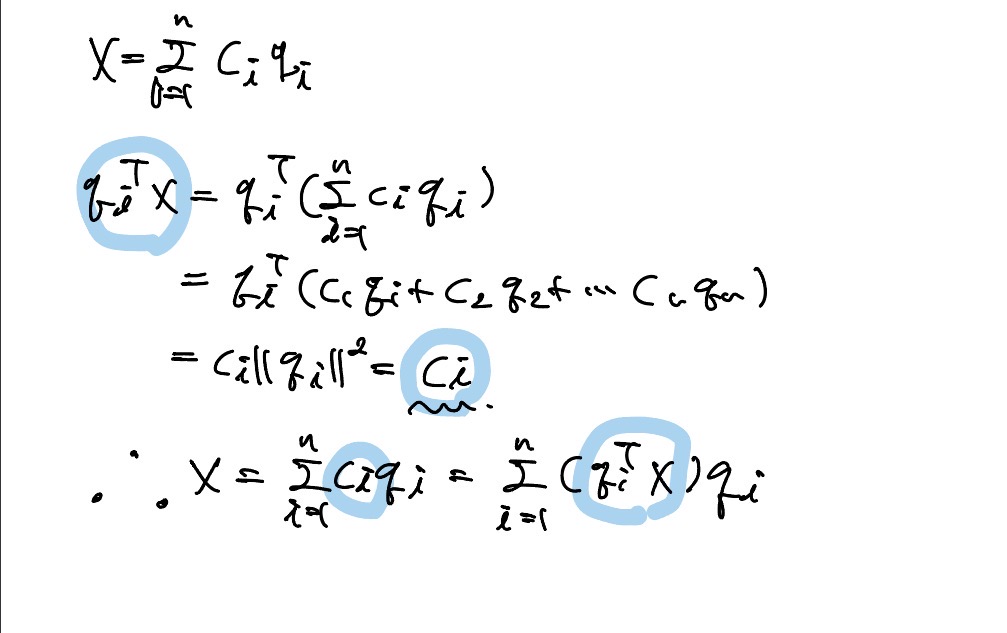
서로 수직이 되는 orthogonal vector들을 통해 basis로 구성하면 선형 결합한 계수는 해당 vector가 각 basis vector에 projection된 크기이다.

Rectangular system

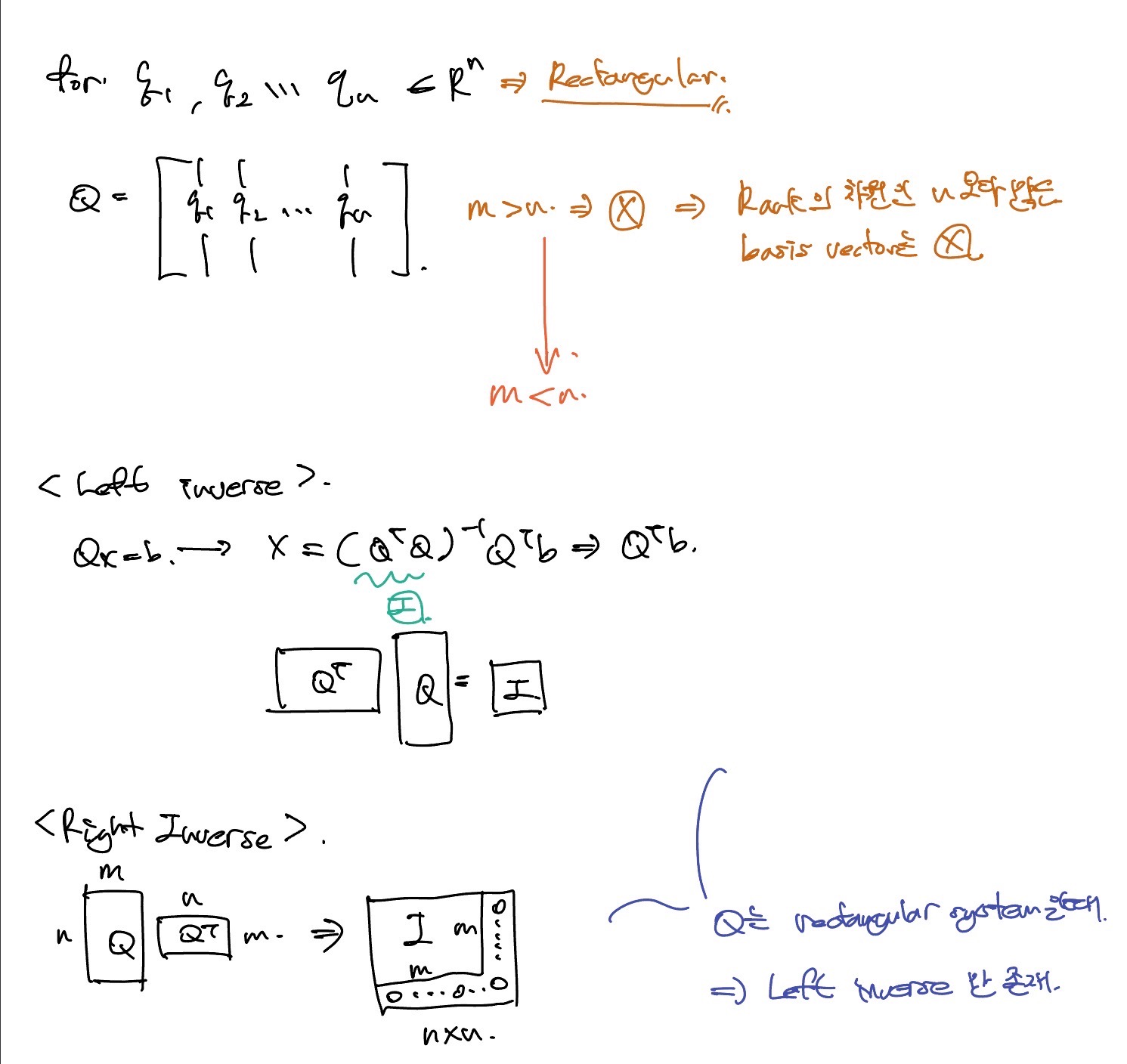
m < n일 경우, left inverse로 square system과 같이 I가 된다.

그러나 m > n일 경우, right inverse로 mxm은 I가되지만 나머지 부분은 0으로 값이 채워지게 된다.

Gram-Schmidt orthogonalization

orthogonal하지 않는 벡터들을 orthogonal하게 바꾸는 방법이 그램-슈미트 직교화이다.

주어진 vector ${a_1, a_2, a_3,...a_n}$에 대해 이 vector들을 생성할 수 있는 직교 vector $q_1, q_2, ... q_n$을 얻는 과정이다. 이러한 과정으로 얻어진 ${a_1, a_2, a_3,...a_n}$은 서로 수직이고 vector space Q = {$q_1, q_2, ... q_n$}에 대한 직교 basis가 된다.

example

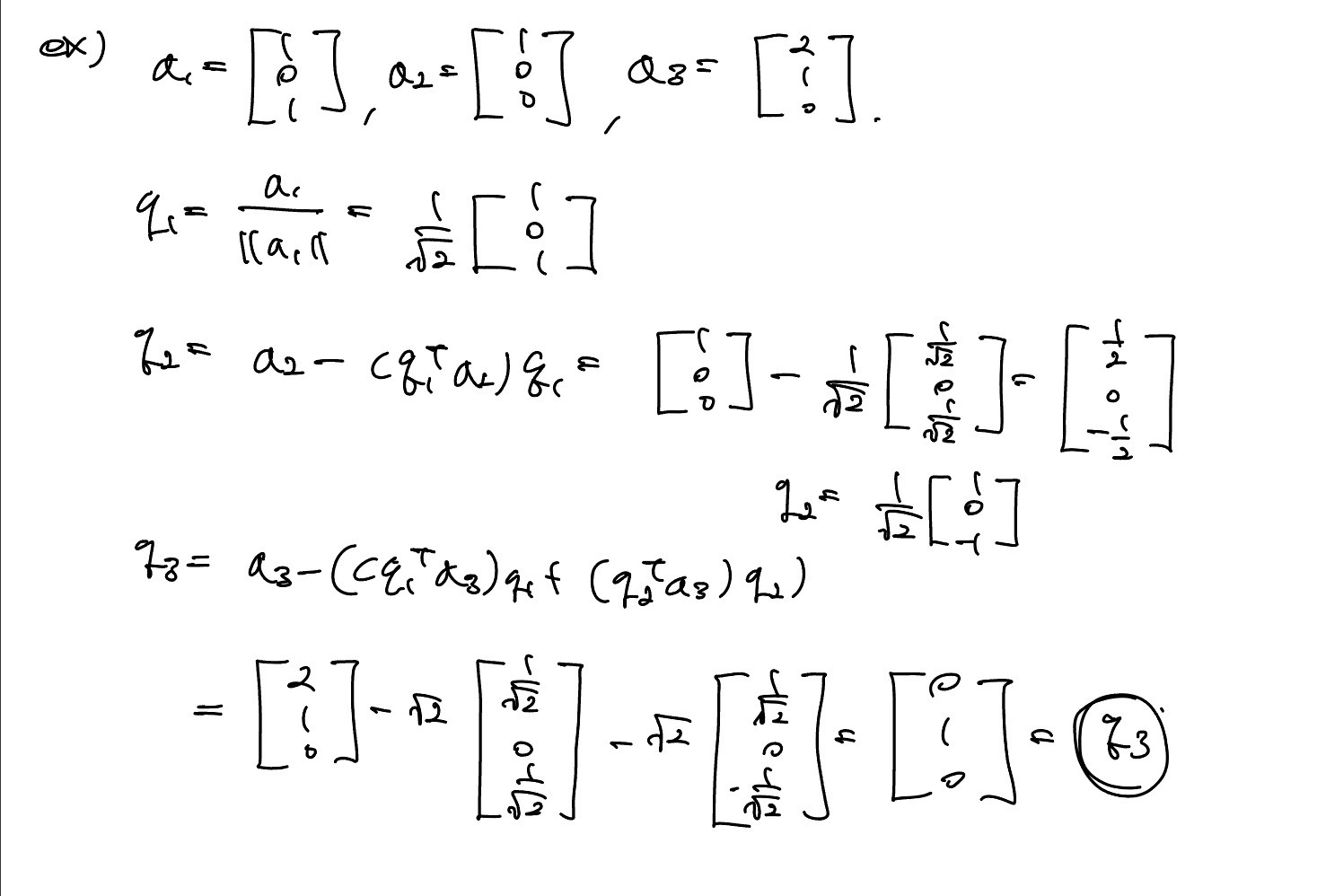
A=QR Factorization

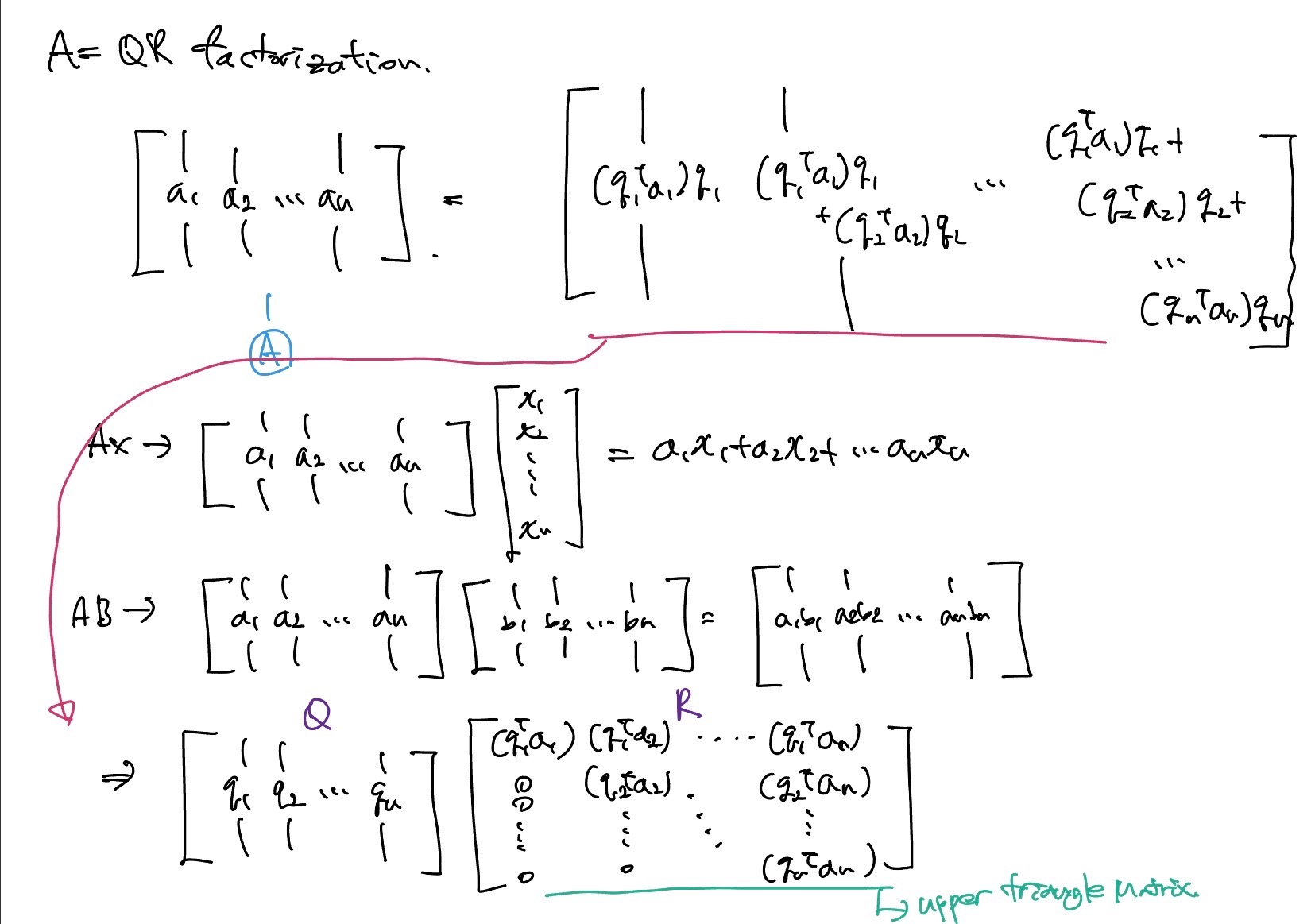
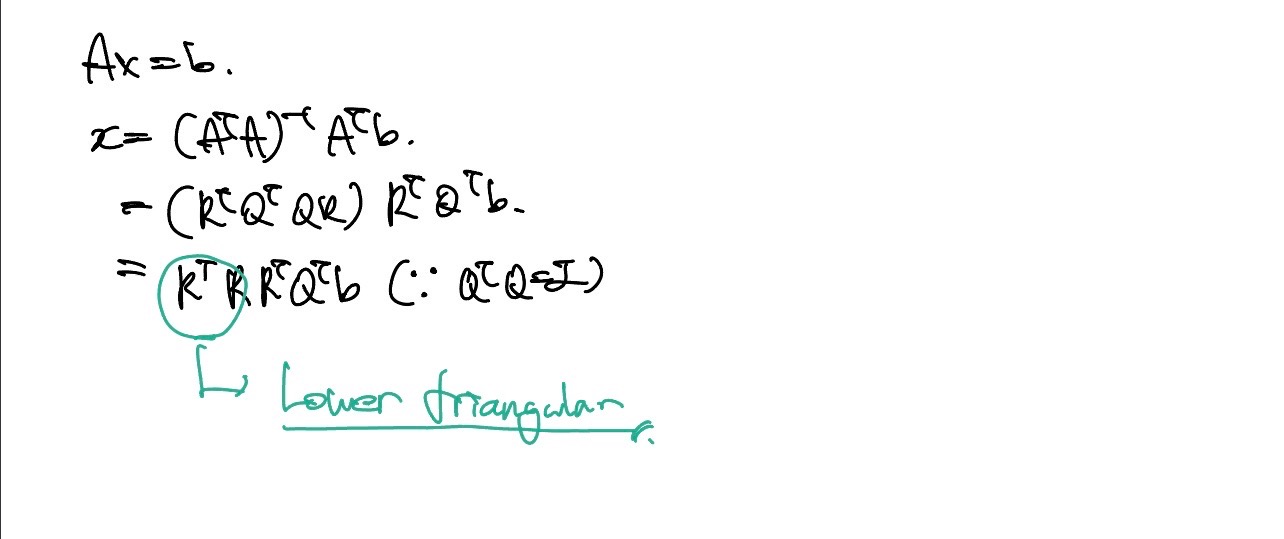
$R=Q^TA$에서 $Q^T$의 i번째 행과 A의 j번째 열이 곱해져서 $R_ij$가 된다. 기존 Least square에서 solution은 $A^TAx = A^Tb$였다. 이 방법으로는 역행렬을 사용해야하는데, 역행렬은 많은 계산량을 요구한다.

위의 식을 이용하면 X는

로 근사값을 통해 적은 계산량으로 구할 수 있다.