12. 1차연립방정식 풀이와 직교벡터 구하기

Review

Square system

Ax=b라는 연립방정식의 solution을 구하는 과정은 3가지를 배웠다.

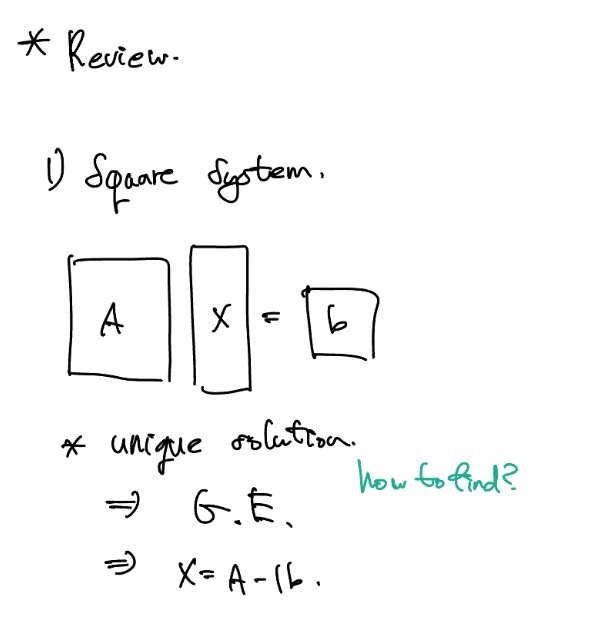
먼저 Square system으로 주어진 방정식을 가우스 소거법을 통해 하나의 unique한 solution을 구했고 만약 solution이 존재하지 않으면 vector space를 통해 solution을 정의했다.

Under constrained system

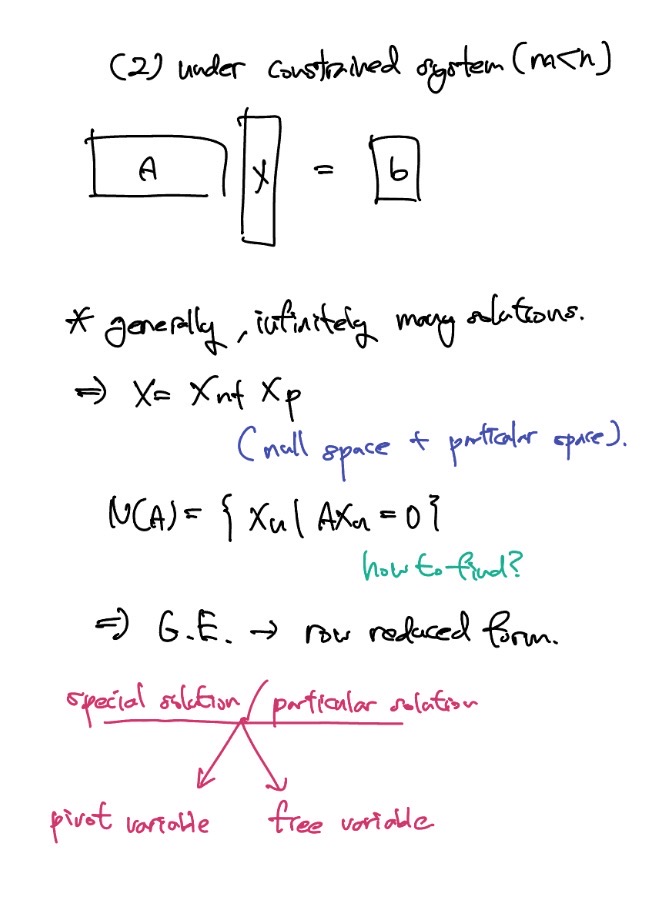
다음은 방정식의 미지수가 방정식(equation)보다 많을 때는 보통 무수히 많은 solution이 존재한다. 이 많은 해는 vector space(null space, particular space)를 통해 정의할 수 있다. 이 역시 가우스 소거법을 통해 row-reduced form로 행렬을 표현하여 special solution과 particular solution 형태로 해를 구해서 pivot variable과 free variable을 나눈다.

Over constrained system

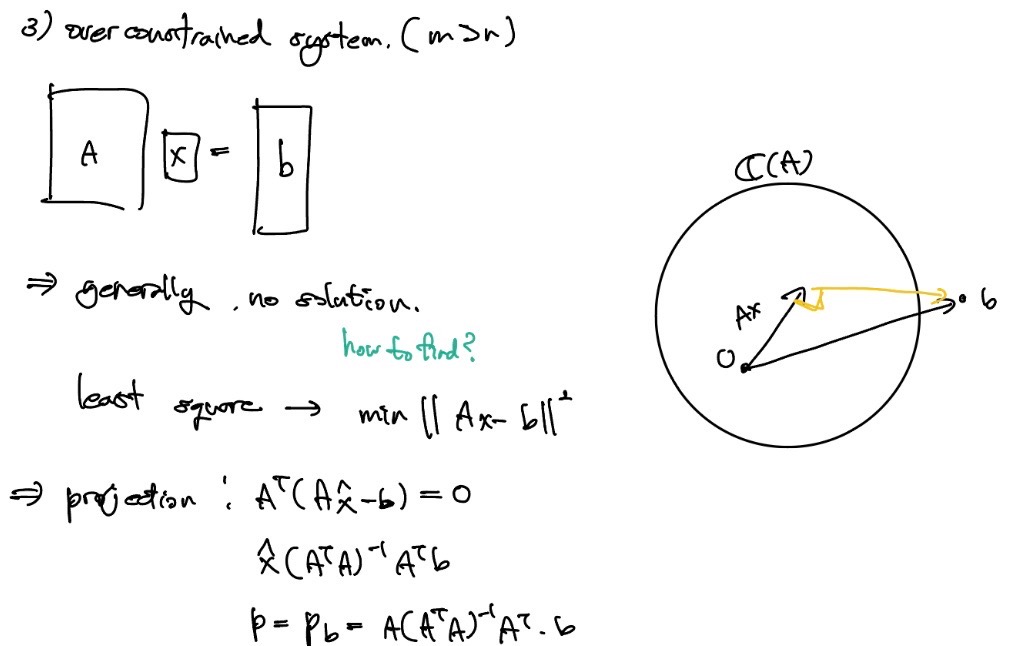
다음은 방정식이 미지수도 많은 경우로 보통 해가 존재하지 않는다. 이때 해를 구할 수 있는 방법으로 vector space가 있다. 행렬 A의 column space에 원점을 지나는 A(x)가 존재하고 b가 column space 외부에 존재한다면 no solution이다.

이때 b와 column space와의 최소 거리를 가지는 vector이 solution이 될 수 있고 least square이다.

b에서 column space에서 수선의 발을 projection하고 이 점을 $A\hat{x}$일 때 vectorsms $A\hat{x}-b$이고 column vector는 $A^T$와 수직이다.

Orthogonal basis vector

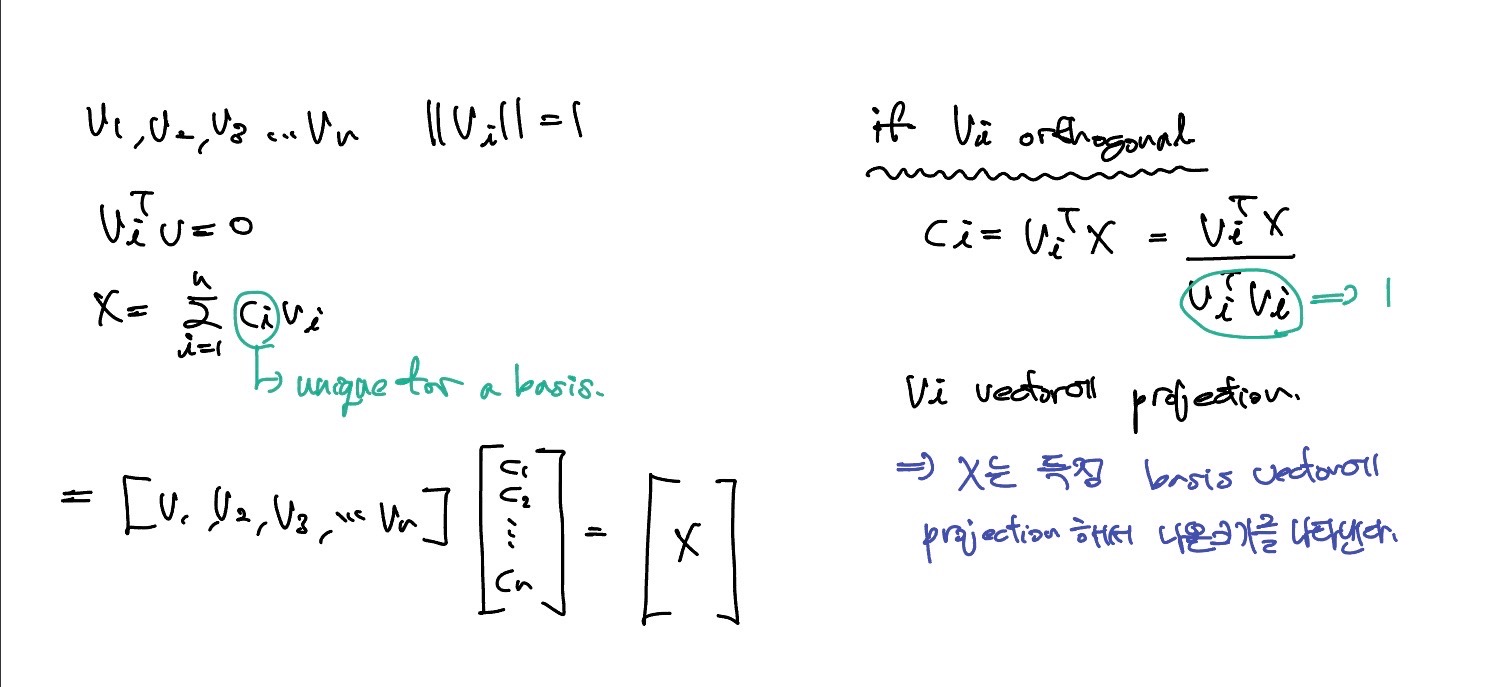
Basis vector를 이용하여 X를 나타내고 수직이라면 projection matrix를 구하기 쉽다.

$v_i$는 linear independent하기 때문에 역행렬이 존재하고 $c_i$는 X에 $v_i$를 곱해 구할 수 있다.

만약 independent한 vector가 주어졌을 때, 직교하는 basis vector를 찾는 방법이 바로 Gram-Schmidt orthogonalization이다.

Gram-Schmidt Orthgonalization

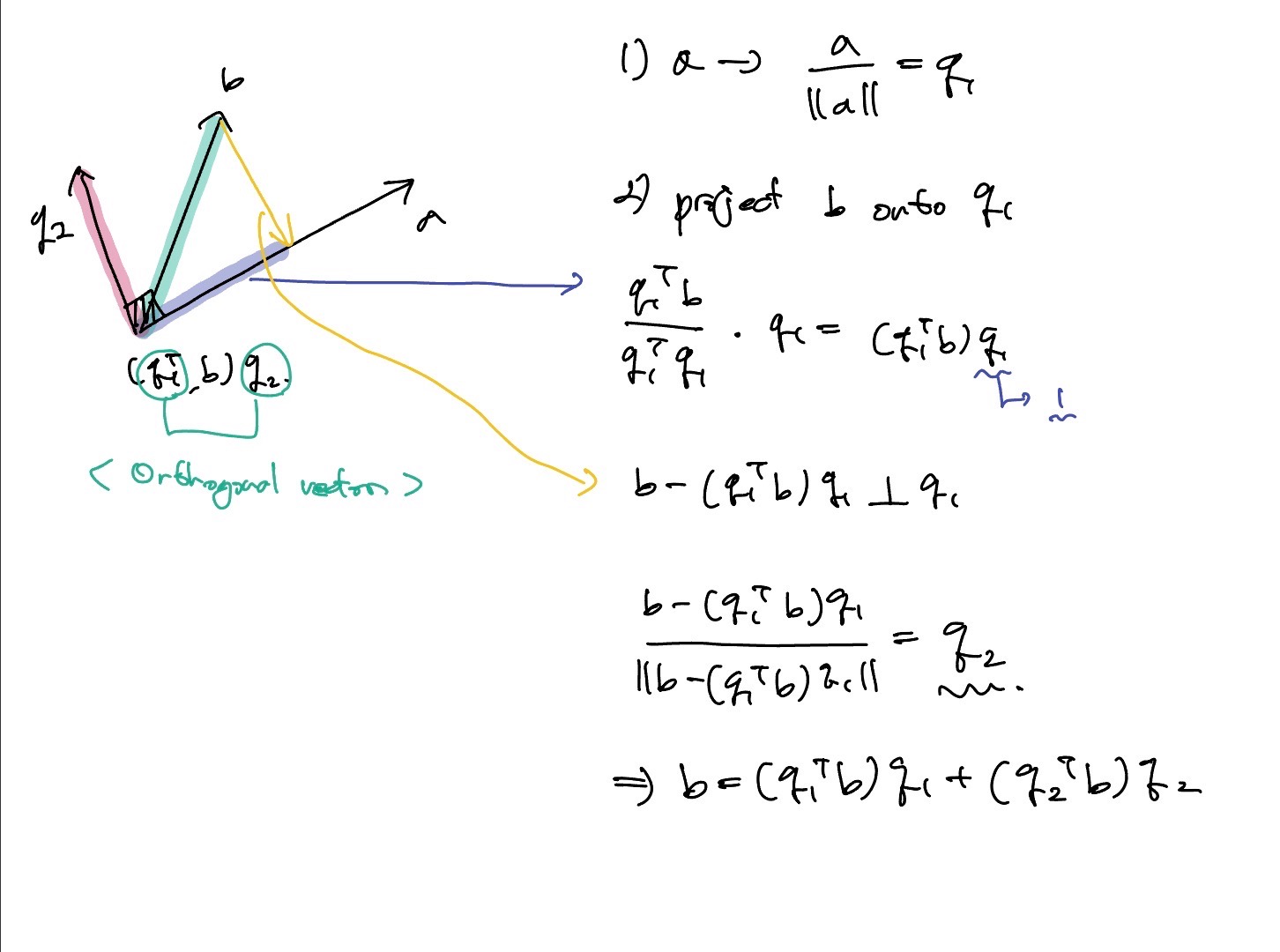
• a vector의 크기가 1이 되도록 normalization
• b vector를 $q_1$에 projection
• 파란색으로 칠한 부분의 크기를 구한다
• $q_2$는 $q_1$과 수직
• $q_2$의 크기를 1로 noramlization
• b vectors는 $q_1$ 방향으로 projection한 vector와 $q_2$ 방향으로 projection한 vector의 합

위의 과정을 정리하면 아래와 같다.

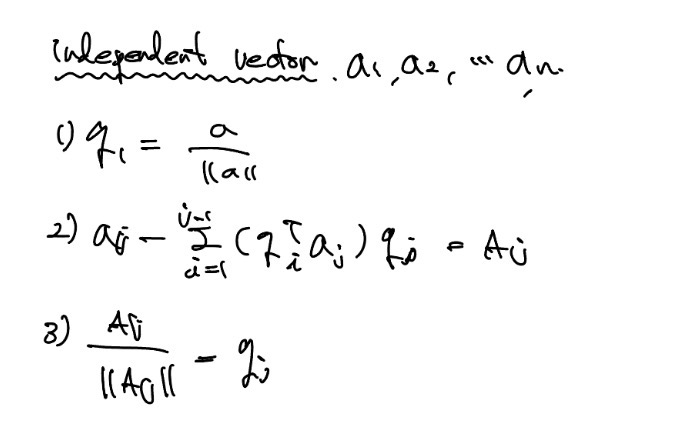
이러한 과정을 직교하는 independent한 vector의 차원 개수만큼 반복한다.

만약 $A_j$의 크기가 0에 가까워지는것은 projection해도 똑같을 때를 의미한다.(이미 space에 있는 점일 때)

최종식은 다음과 같다.

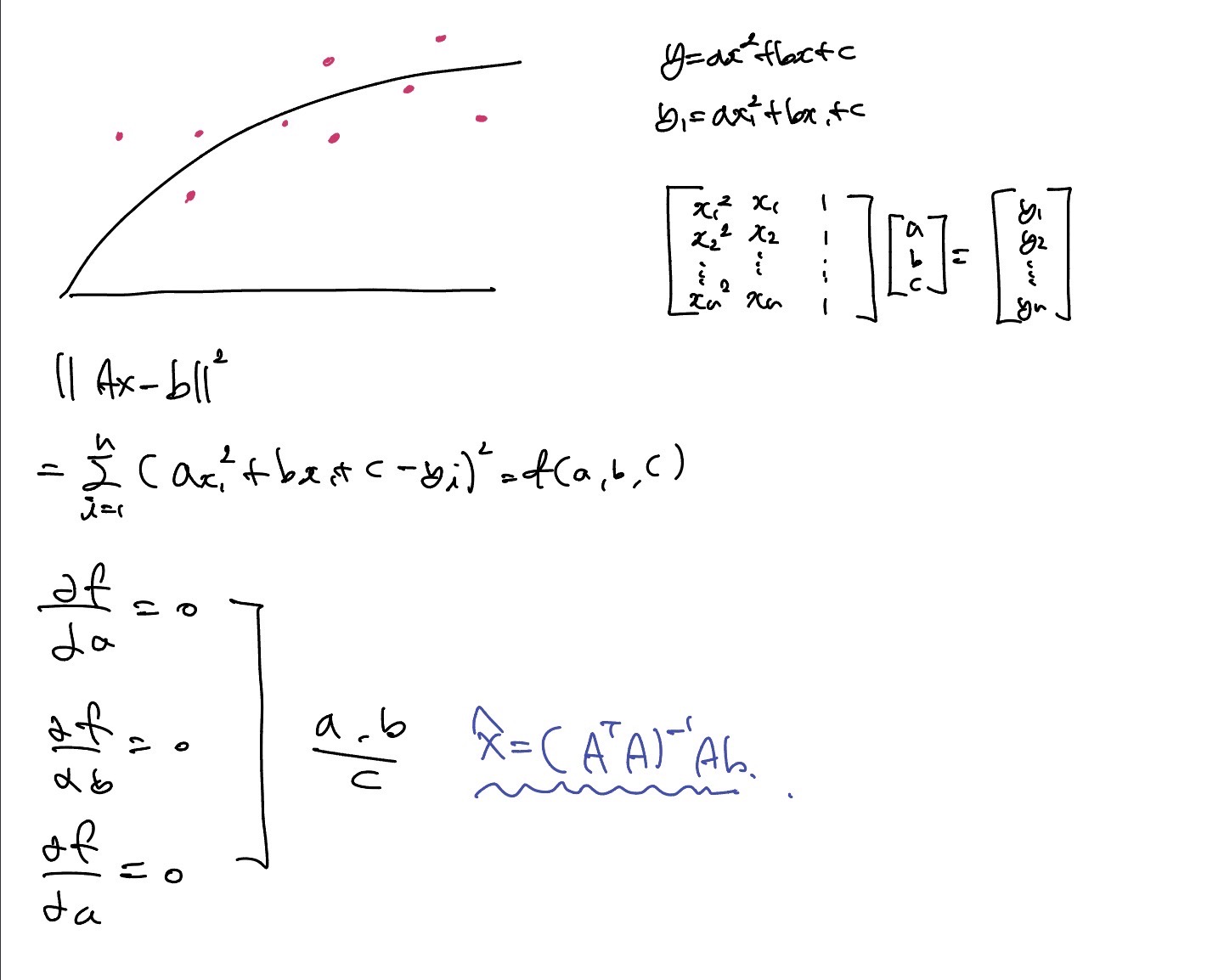
Line fitting

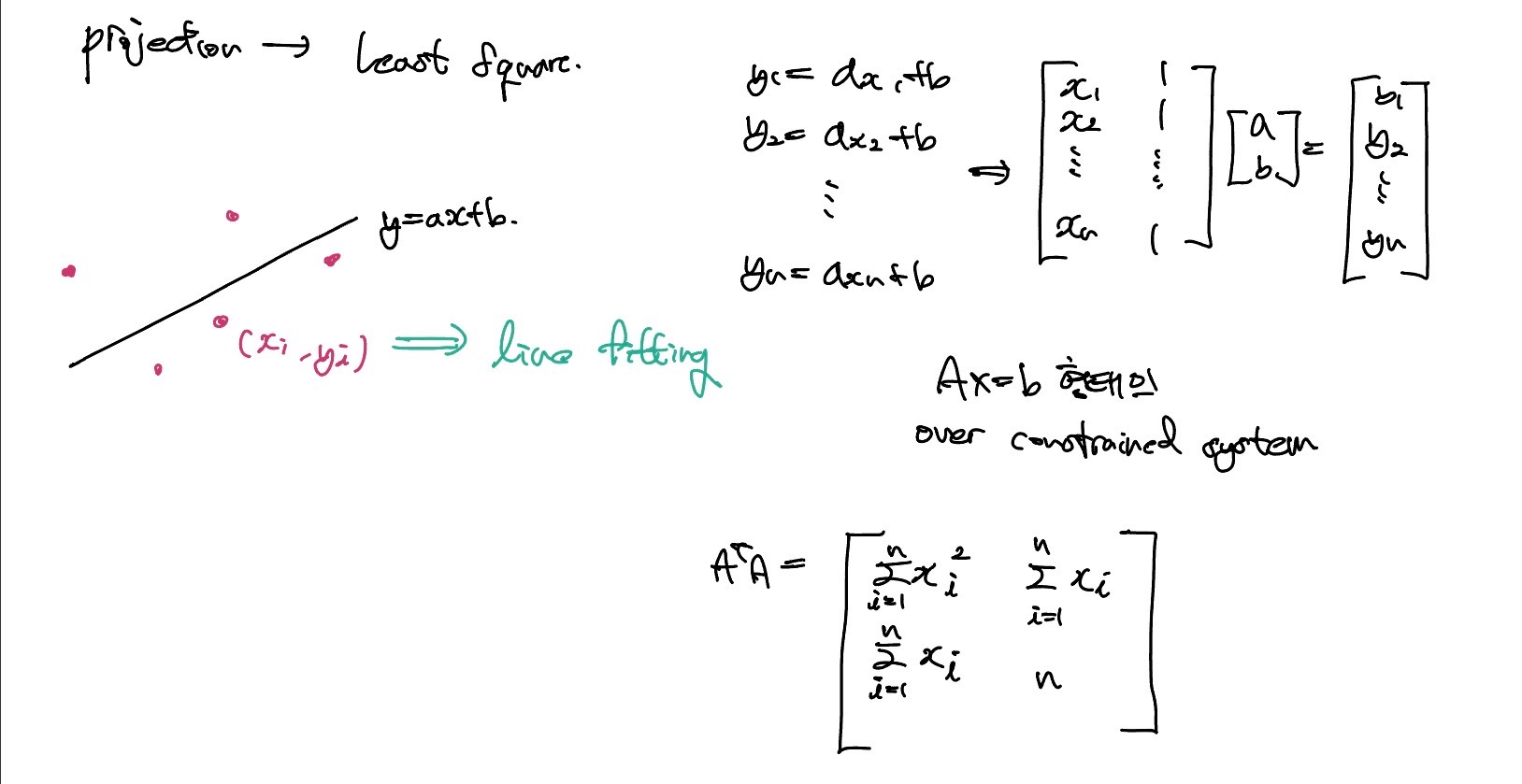
주어진 모든 점을 가장 적은 error로 fitting할 수 있는 선이 필요하다. Line fitting이 일어나면 over constrained system의 형태를 보이고 projection을 통해 미지수를 구할 수 있다.

X라는 vector를 구하기 위해 먼저 $A^TA$ 행렬을 구하고 A와 b의 값을 구하면 가장 가까운 직선을 구할 수 있다.

편미분을 통해 구할 수도 있다.

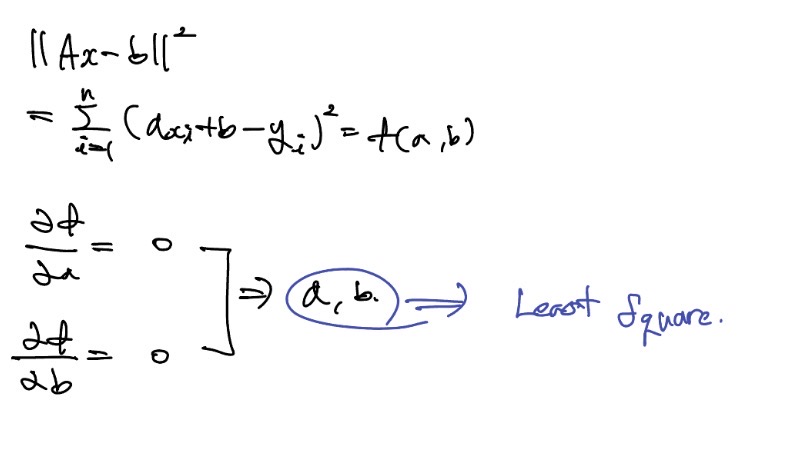
직선이 아닌 곡선에 대해서 fitting할 때는 다음과 같다. (Least square, 미분)