4. Inverse and Transpose

홍종현·2022년 5월 8일
0

Linear Algebra

목록 보기
4/14

역행렬과 전치행렬은 모두 정사각행렬(nxn)을 가정한다.

역행렬의 정의

AA−1=A−1A=I,(AB)−1=B−1A−1AA^{-1} = A^{-1}A = I, (AB)^{-1} = B^{-1}A{-1}

-> 하지만 모든 matrix에 역행렬이 존재하는것은 아님.

가우스 소거법의 결과로 U행렬에 n개의 pivot이 생길 때, 존재한다.

다음은 역행렬의 특징에 대해서 정리했다.


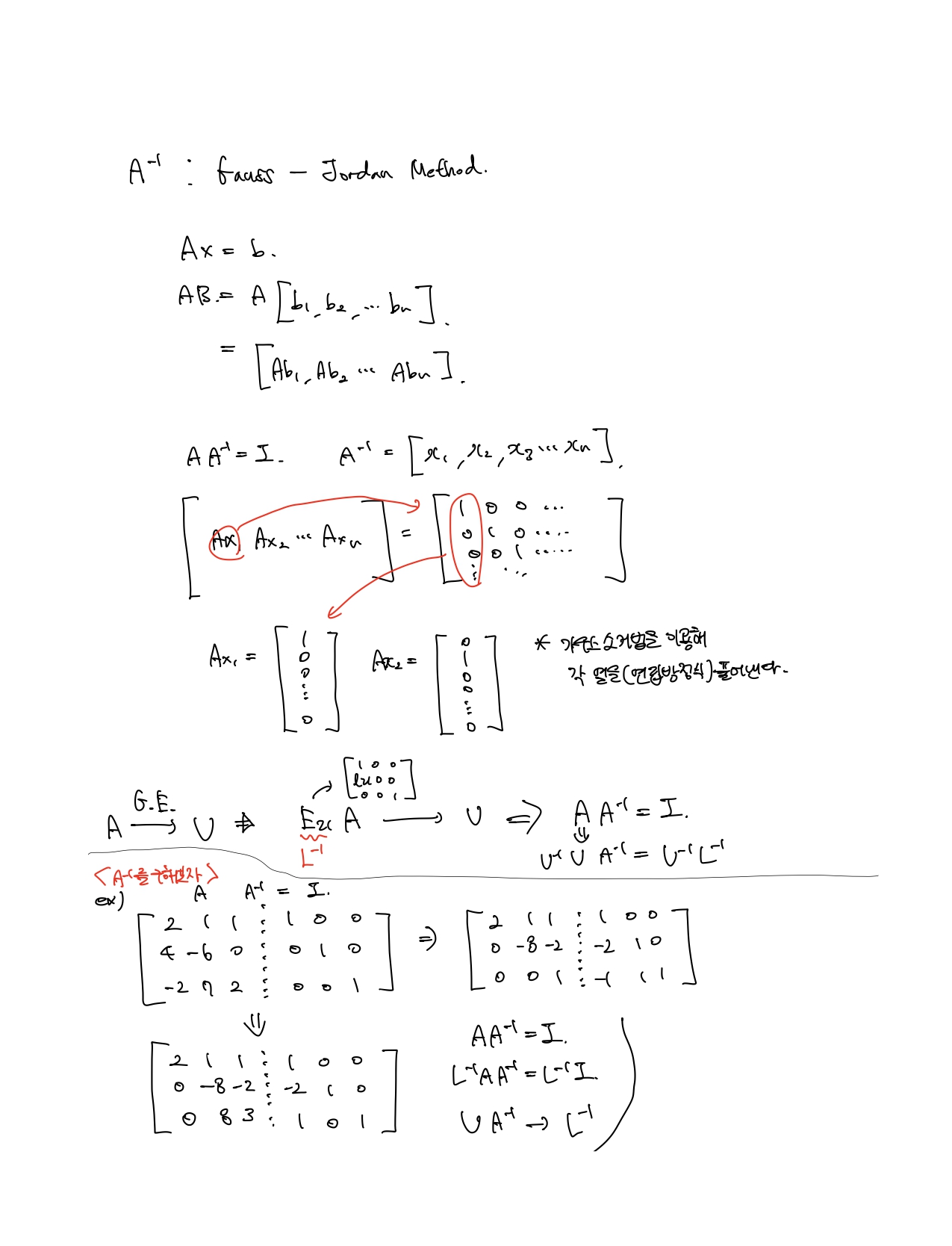
결국 AX = I이기 때문에 가우스 소거법을 응용할 수 있다. 가우스 소거법의 결과로 U 행렬에 n개의 pivot이 생길 때만 역행렬이 존재한다. => Non-singular의 경우에만 역행렬이 존재한다.

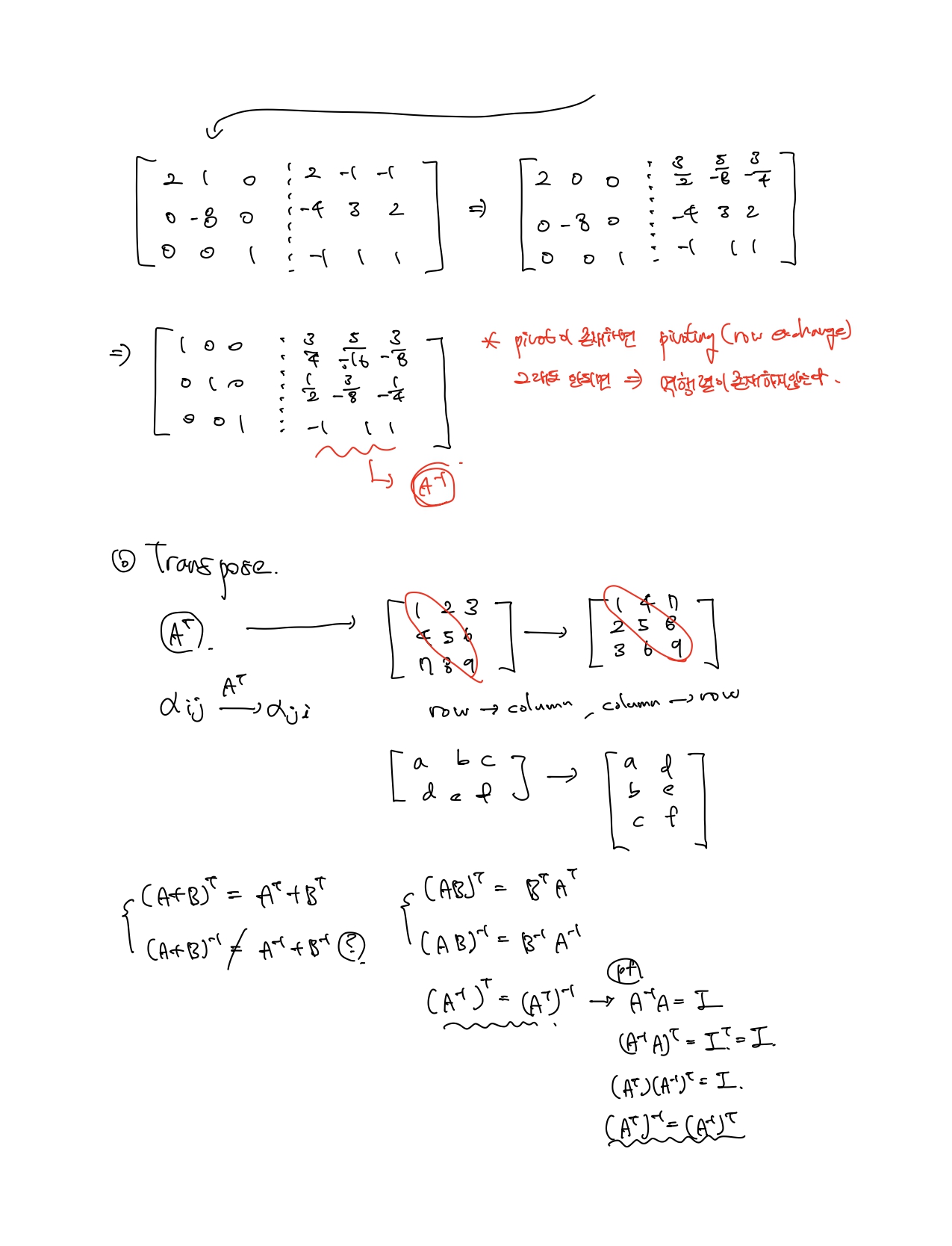
역행렬을 구하는것이 쉽지않다.

A가 대칭행렬이고 역행렬이 존재한다면, A의 역행렬도 대칭행렬이다.

AA−1=l(AA−1)T=lT=l(A−1)TAT=(A−1)TA=IAA^{-1} = l (AA^{-1})T = l^T = l (A^{-1})^TA^T = (A^{-1})^TA = I

A가 대칭행렬이고, A = LDU일때, A=AT=UTDTLT=LDLTA = A^T = U^TD^TL^T = LDL^T이다.
U와 L 둘 중 하나만 알면 쉽게 구할 수 있다.

profile
홍종현
이전 포스트

3. LU decomposition

다음 포스트

0. Linearity Basic

0개의 댓글