3. LU decomposition

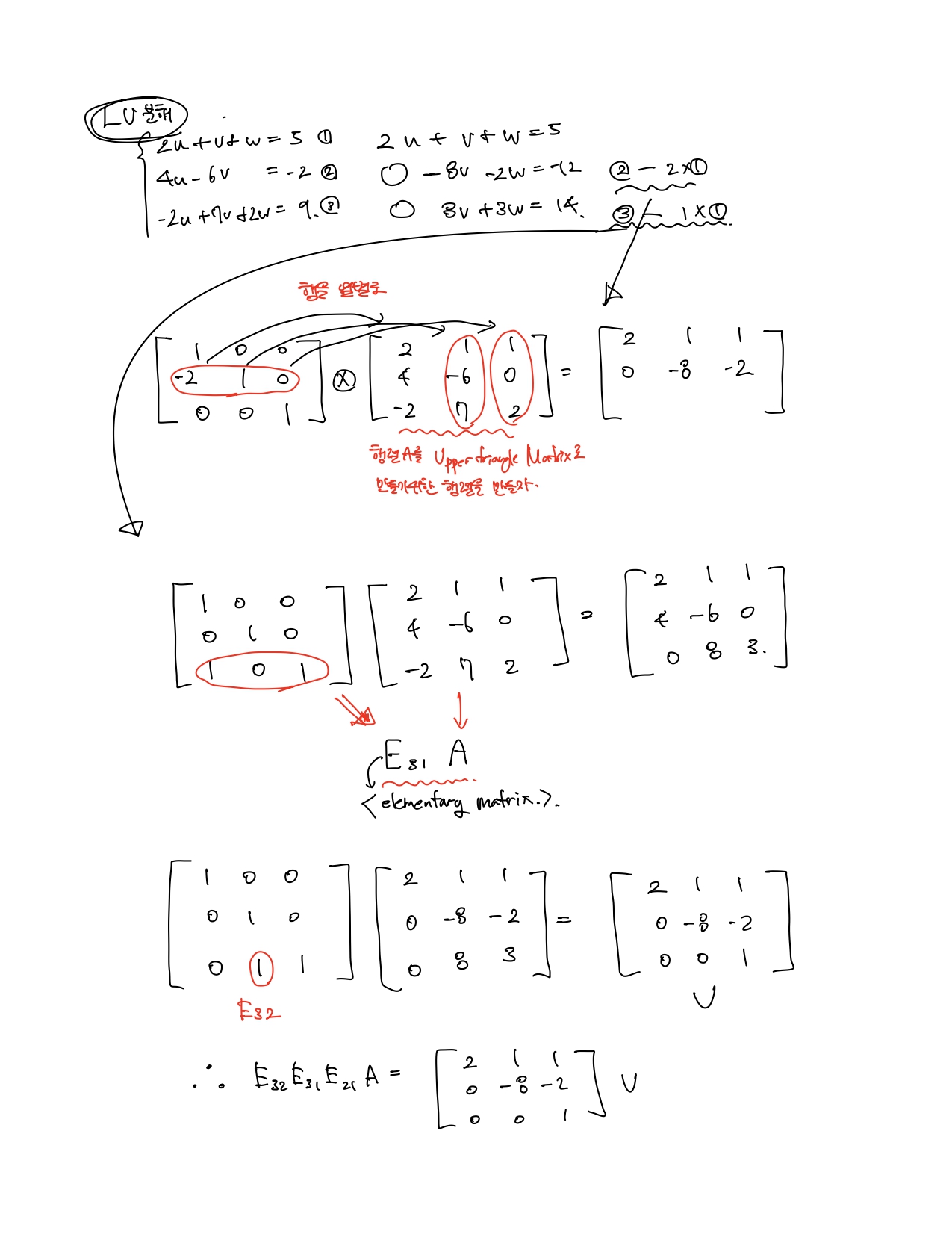
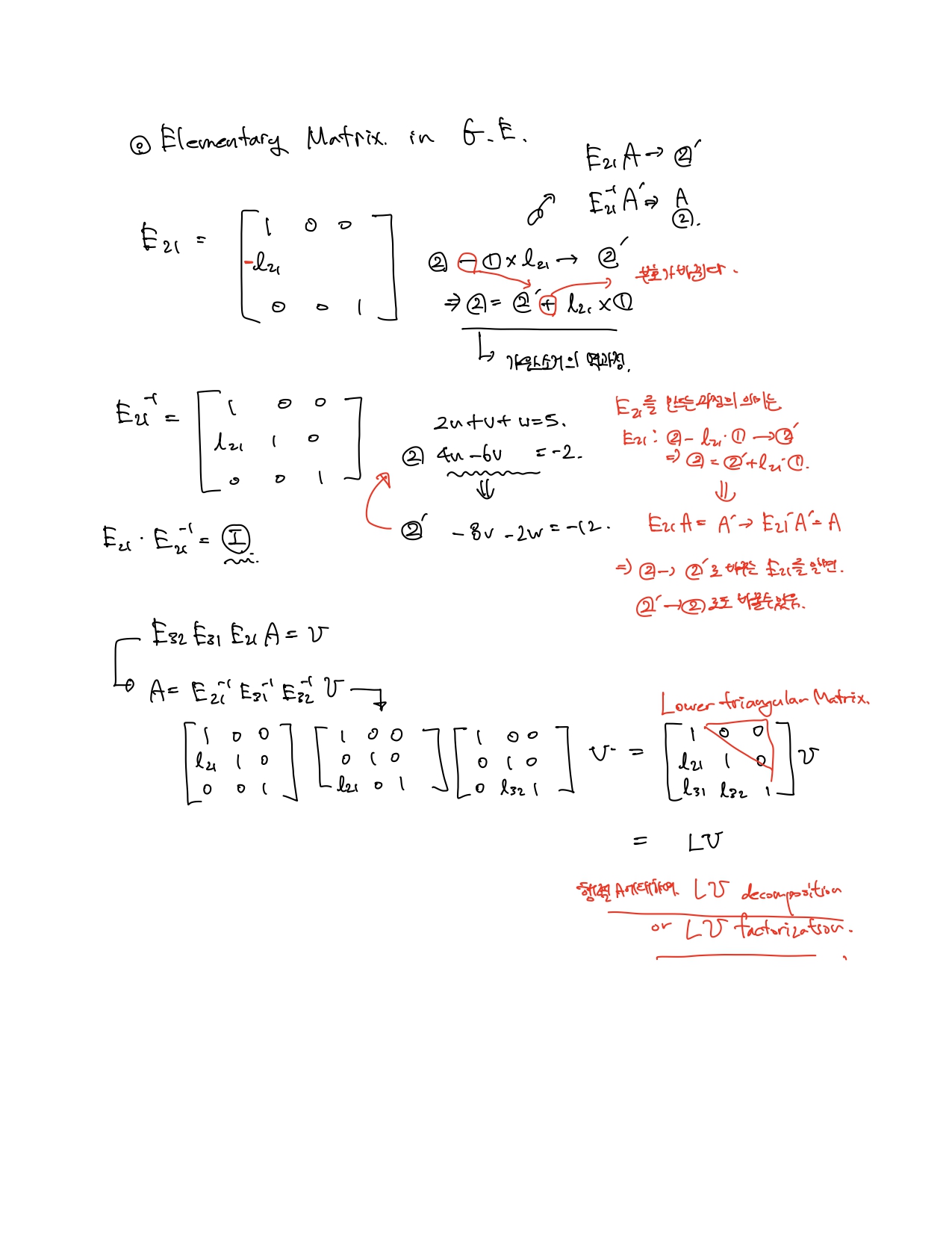
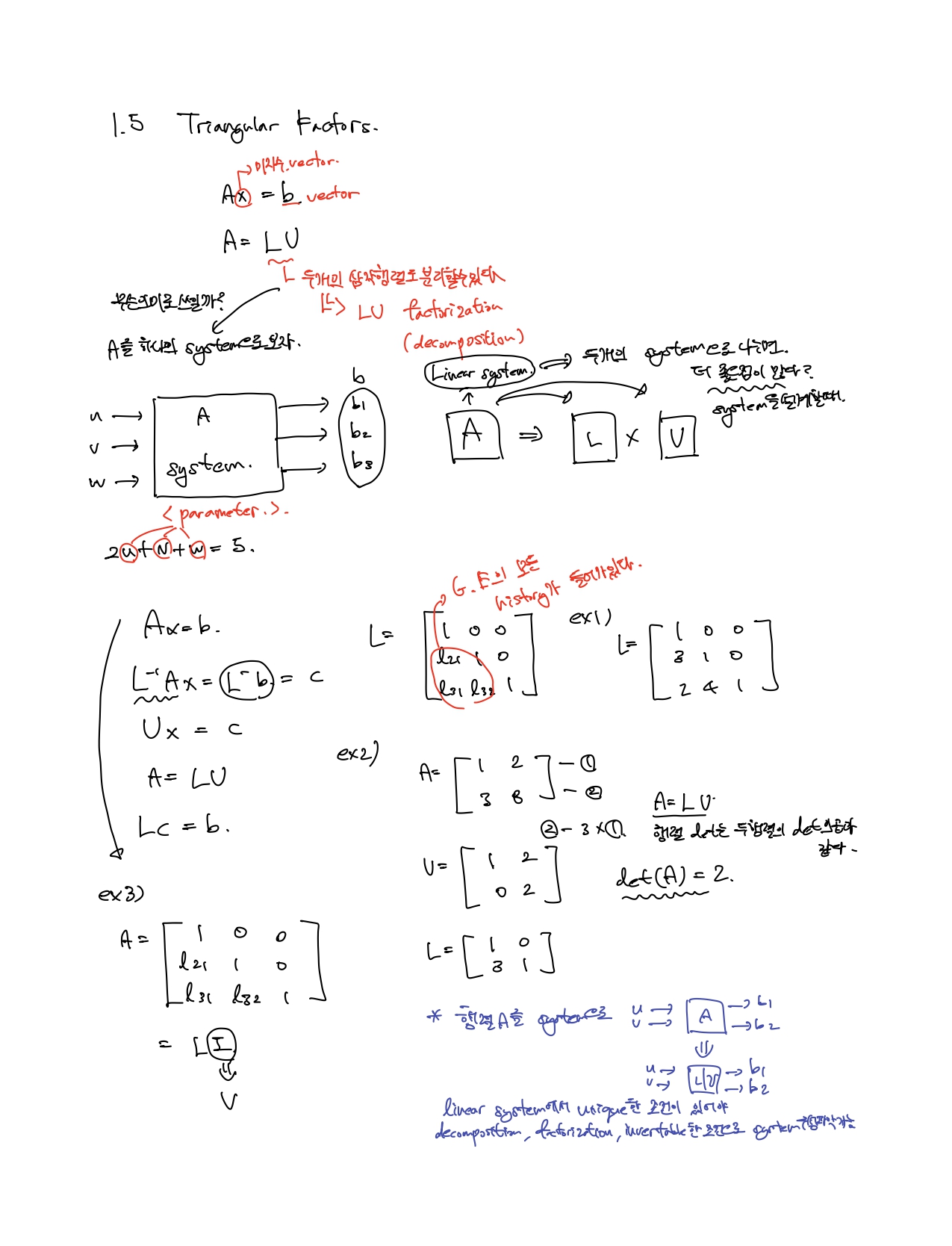
LU분해란 하삼각행렬과 상삼각행렬의 곱으로 표현하는 것이다. 하삼각행렬은 주대각선을 기준으로 위에가 전부 0인 행렬, 상삼각행렬은 주대각선을 기준으로 아래가 전부 0인 행렬이다.

1. Ax=b를 LUx=b로 표현한다.
2. 새로운 vector y를 Ux=y로 정의하고, LUx=b를 Ly=b로 표현한다.
3. 선형계 Ly=b를 기존의 방법으로 풀어 y를 구한다.
4. 구한 vector y를 Ux=y에 대입한 뒤, 이 선형식을 기존의 방법으로 풀어 최종 x를 구한다.

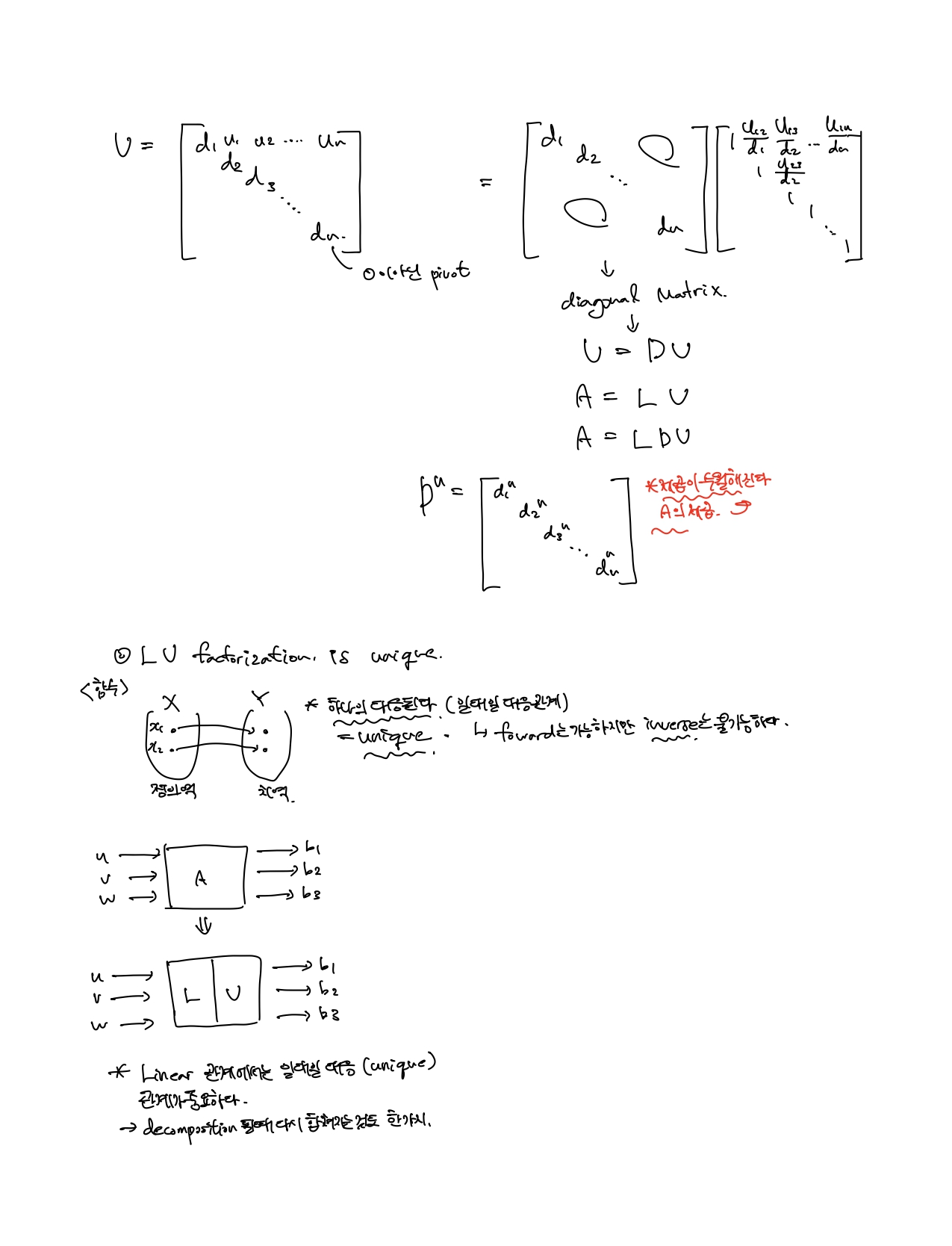
LU factorization은 모두 unique하다.(일대일 대응이다.)

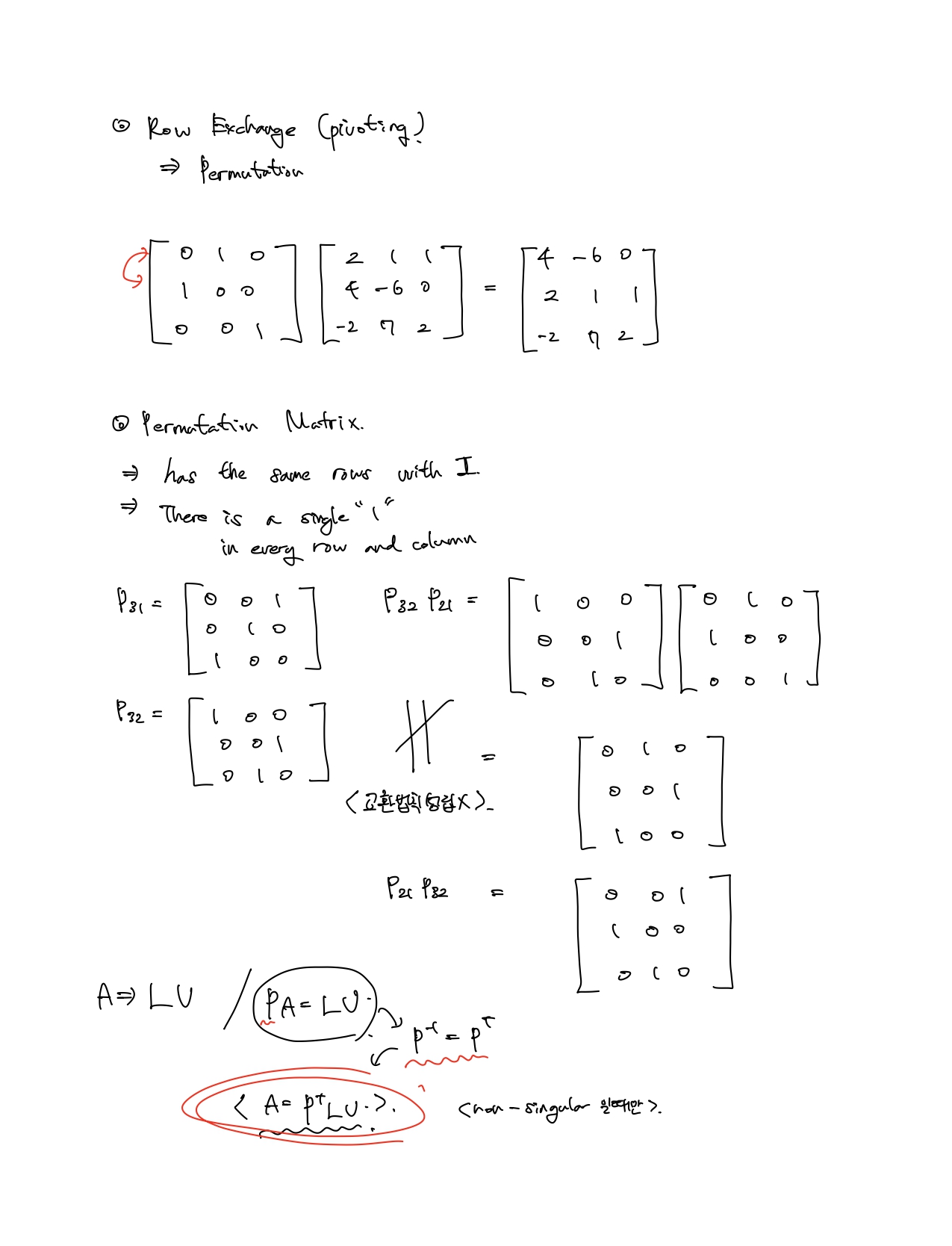
Permuatation Matrix P는 I에서 위치를 변경할 두 행을 뒤바꾼 형태이다.

• In the non-singular cases, there exists a permutation matrix P, and PA = LU.
• In the singular cases, there is no P, and elimination fails.