5. Vector space and Column space of vector

기존에는 #of unknowns = # of equations의 경우를 구했지만, 이제부터는 #of unknowns > # of equations의 경우 해를 구하는 법을 배우게 된다. 즉 직사각행렬에 대한 해를 구하게 된다. 이럴경우 무수히 많은 해와 해가 없음으로 나뉘게 된다.

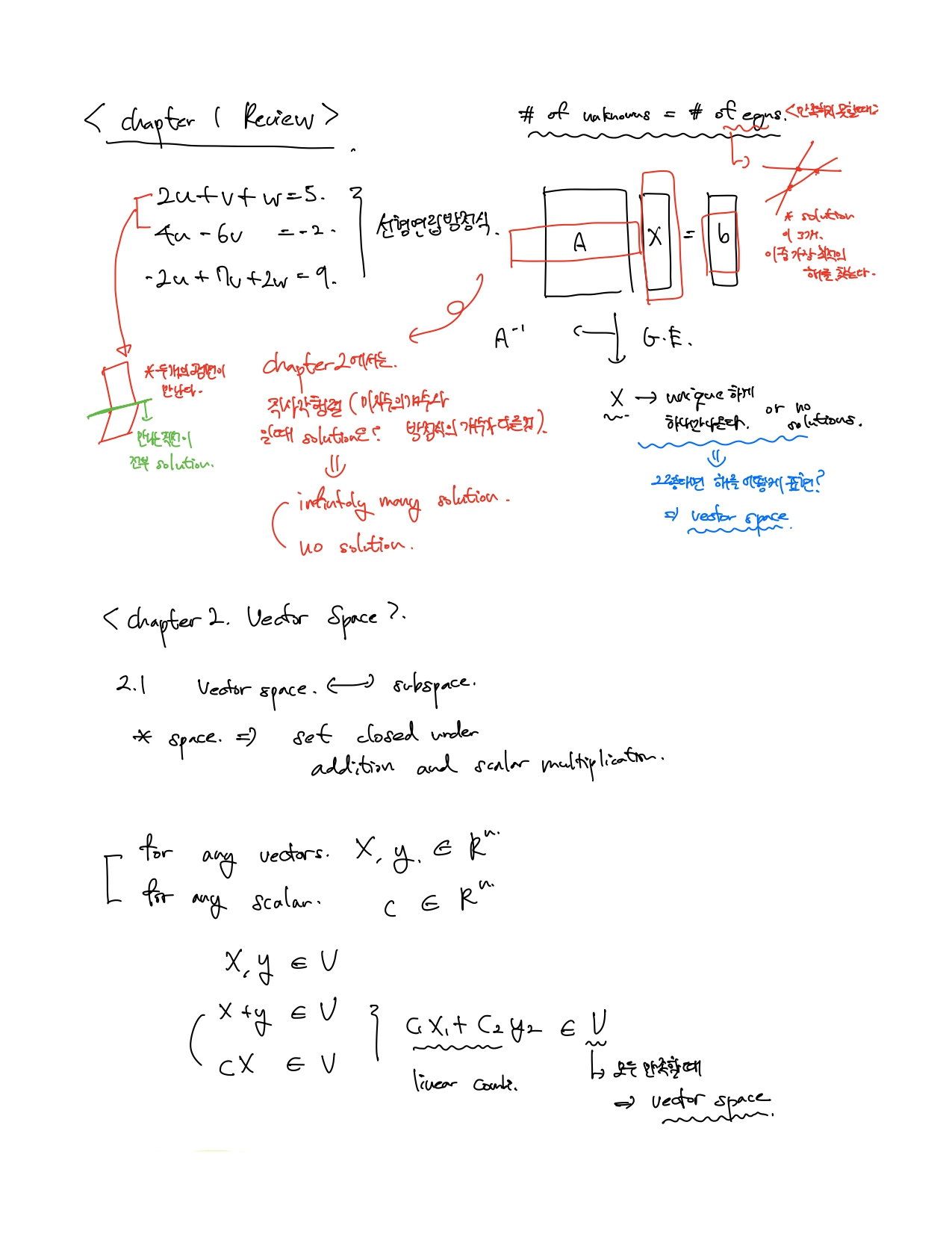
$Ax =b$라는 연립방정식을 풀 때, 정사각행렬을 기반으로 했다면, 이번에는 식의 개수가 미지수의 개수보다 적은 경우를 가정한다.
$mxn$행렬에서 $m\le n$이라면 표현해야 하는 미지수보다 식의 개수가 적기 때문에 non-singular한 상황은 나오지 않을것이다.

테일러 급수에 대한 얘기가 잠깐 나왔다. 테일러 급수(Taylor series)란 아래의 식으로 표현할 수 있다.

테일러 급수는 $x=a$에서 f(x)와 동일한 미분계수를 갖는 어떤 다항함수로 f(x)를 근사시킨다. 다시 말하면, 비선형함수를 1차식 또는 2차식으로 표현할 수 있다.

즉, $f(x) = e^x$를 다음과 같이 표현할 수 있다.

다항식을 vector로 표현할 수 있는데, 저 계수들이 vector의 element가 된다.

x와 y가 뎃셈과 scalar 곱에 대해 닫혀있을 때, 이를 vector space라고 부른다. 또한 벡터 공간의 조건을 만족하는 부분집합(Subset)을 Subspace라고 부른다. 벡터 공간과 부분공간은 반드시 원점을 포함해야한다. 원점을 지나지 않으면, linear combination이 성립하지 않는다. 원점은 가장 작은 부분공간으로 볼 수 있다.

방정식을 푼다는것 자체가 A의 column vector의 조합으로 b를 만들 수 있는 계수 $x_1, x_2, ..., x_n$을 찾는것을 의미한다. 만약 b가 애초에 A의 column vector의 조합으로 만들 수 없다면, b가 C(A)에 포함되지 않는다면 해당 연립방정식은 해가 없는, no solution이다.

$Ax=b$에서 A의 역행렬이 존재한다면, 당연히 해도 존재하고 $x = A{-1}b$이다.

• 해가 존재한다는 것은 $b \in C(A)$
• C(A)는 whole space

b가 C(A)에 포함되기 때문에, vector space의 부합한다.

• $A(x+x') = b + b'$ -> closed under addition
• $A(cx) = c(Ax) = cb$ -> closed under scalar multiplication