Review

Subspace는 vector space의 조건을 만족하면서, vector space의 부분집합이 되는 space를 의미한다. 또한 하나의 vector는 무조건 0-vector여야한다.
Column Space of A(열벡터 공간)은 행렬에 존재하는 모든 column vector의 선형결합들의 모든 집합을 의미한다.
Null Space

Null space는 두가지 성질이 있다.
- closed under addition
모든 덧셈에 대해 닫혀있다.
- closed under scalar multiplication
scalar 곱에 대해 닫혀있다.
Solving Ax = 0 and Ax = b
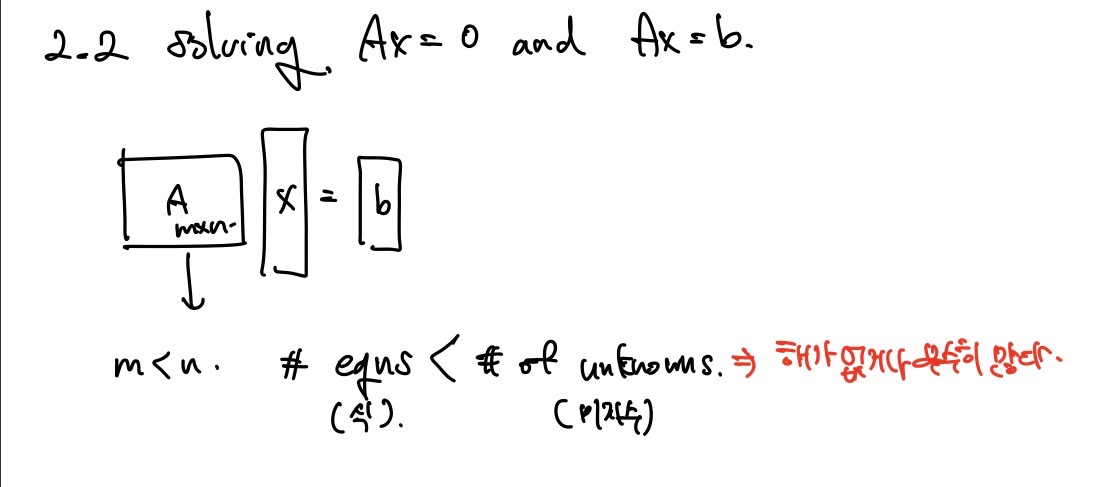
기존에는 정사각행렬을 풀었지만, 행과 열이 다른 직사각행렬의 해는 없거나 무수히 많다.
공간상의 두 평면이 존재한다고 했을 때, 두 평면이 한 직선에서 만나는 경우는 해가 무수히 많은 경우이고 두 평면이 평행한 경우는 해가 없는 경우라고 생각하면 된다.
Echelor from U
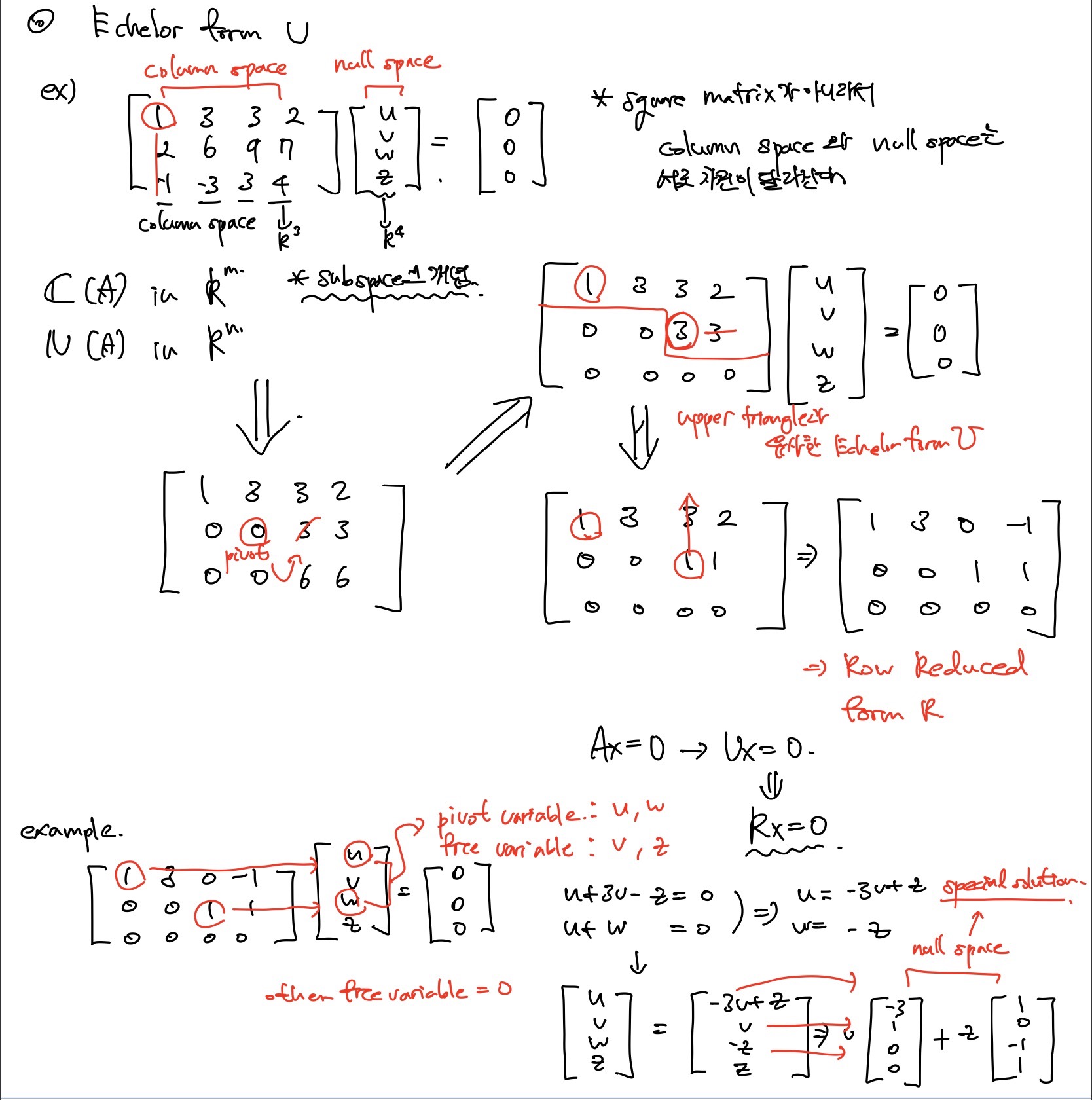
기존 Ax=b를 풀때와는 다르게 b는 zero vector니까 A를 이용해서 풀면 된다. 가우스 소거법을 이용해서 해를 구할 수 있는데 기존에는 가우스 소거법으로 풀면 해가 있가 있고 해가 없었다면, 직사각행렬에서는 해가 무수히 많거나 해가 없다. 이러한 무수히 많은 해의 집합은 vector space를 이룬다. Row-reduced form으로 나타내고 pivot이 존재하는 column의 변수를 pivot variable이라고 하며 나머지는 free variable이라고 한다.

u,v,w,z는 4차원의 null space를 구성하는 X vector를 구하는데 임의의 linear combination으로 구할 수 있고 free variable로 구성되어 있다.
그리고 special solution vector의 차원이랑 미지수의 차원이 맞지 않아 dimension을 정의해야한다.