Introduction
지난 강의에서는 word embedding 기법 중 하나인 Word2Vec에 대해서 공부했다. Word2Vec을 통하여 단어간의 의미 관계를 벡터 공간에 표현할 수 있다. 중심단어(center word)와 주변단어(context word), 두개의 벡터를 내적값을 구하여 softmax를 통해 확률을 계산했다.
Optimization
Word2Vec를 학습할 때 gradient descent를 사용하여 를 backpropagation을 통하여 최소화하는 방향으로 업데이트를 한다.
이 식의 는 step size 혹은 learning rate를 의미하고 gradient의 negative 방향으로 이동하며 파라미터를 업데이트한다.
그러나 위와 같은 gradient descent는 문제점을 가지고 있다. Word2Vec은 해당 업데이트에 사용하는 단어들만 gradient를 가지고 있다. 그러나 Gradient Descent로 학습을 하면 전체 corpus의 단어에 대한 계산을 해야하기 때문에 연산량이 많고 시간이 오래걸린다.
따라서 Stochastic Gradient Descent로 학습을 진행하는데 SGD(Stochastic Gradient Descent)란, loss function을 계산할 때 전체 데이터가 아닌 일부 sampling한 데이터에 대해서만 loss function을 계산하여 update하는 방식이다. Word2Vec은 one-hot encoding의 입출력 형태를 가지고 있어 SGD를 적용하면 윈도우 사이즈에 없는 단어들은 업데이트가 되지않아 sparse한 gradient를 update하여 불필요한 계산이 이루어진다.
Word2Vec model
Skip gram
Skipgram은 중심단어를 이용하여 주변단어를 예측하는 모델이다.
C-BOW(Continuous Bag of Words)
C-BOW는 주변단어를 통해 중심단어를 예측하는 모델이다. C-BOW는 model이 이진분류로 간단해질 수 있고 업데이트를 많이할 수 있어 좋은 임베딩 벡터를 얻을 수 있다.
The skip-gram model with Negative sampling(SGNS)
Word2Vec은 output layer에서 출력된 값에 softmax 함수를 적용하여 확률값으로 변환하는 구조이다.
그러나 softmax를 적용하면 분모에서 모든 단어에 대한 내적 값을 구해야하기 때문에 연산량이 크다는 문제점이 있다. 이러한 문제점을 해결하기위해 실제 중심단어의 실제 주변단어와 주변단어가 아닌 단어를 이진분류하는 binary logistic regressions 학습하는 방법을 이용한다. 이때 주변단어가 아닌 단어들은 임의의 분포를 가정하여 negative sampling을 진행하는데 다음과 같은 식을 통해 가정한다.
U(w)는 코퍼스에서 각 단어의 등장 횟수이다. 등장횟수에 3/4승을 입혀 각 단어간의 횟수 차이를 줄여준다. Z는 단순한 normalization term으로 모든 단어의 U(w) 3/4승의 합으로 각 단어간의 등장 횟수를 나누어 확률 분포를 생성한다. 이 식을 통해 등장하는 빈도수가 높은 단어는 샘플링되는 횟수가 많을것이다. -> (값이 커지기 때문에)
이 모델의 목적함수는 다음과 같다.
먼저 우변의 첫번째 항을 보면 sigmoid 함수가 반환하는 값은 0에서 1 사이이기 때문에 log0에서 log1사이가 된다. 다시말하면, sigmoid 함수를 통해 나온 값이 클수록, 주변단어의 벡터와 중심단어의 벡터의 내적값이 클수록 는 0에 가까워진다.
우변의 두번째 항은 반대로 오답쌍에 대한 연산으로 볼 수 있는데 음수를 곱하기 때문에 내적값과는 반대로 연산이된다. 정리하자면, center word()와 context word()가 같이 나올 확률이 높으면 는 0에 가까워지고 반대로 negative sampling한 단어쌍이 나올 확률이 낮으면 또한 는 0에 가까워진다.
Co-occurrence Matrix
아래 그림은 window size가 1인 co-occurrence matrix이다. 문장 하나를 기준으로 window size안에 단어의 등장 횟수를 세어 표기한다. 이 행렬은 대각을 기준으로 대칭하는 구조를 가지고 있어 좌, 우에 대한 정보는 가지고 있지 않다.
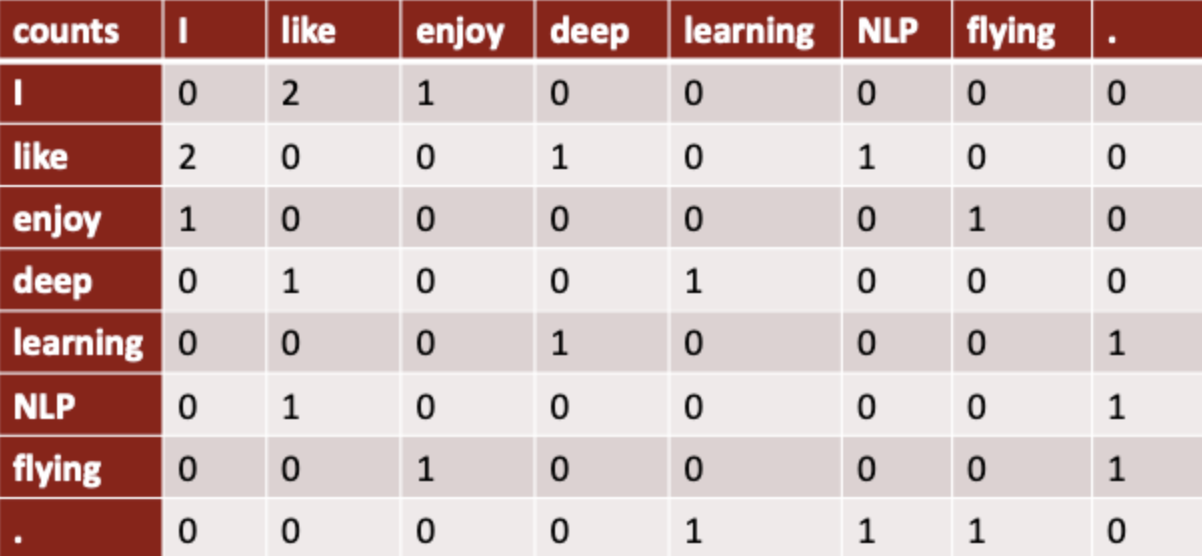
이렇게 나타냈을 때, 비슷한 의미를 가진 단어끼리 비슷한 벡터를 가지게 됨을 알 수 있다. 각 단어마다 주변단어가 비슷한것을 알 수 있기 때문이다.
하지만 동시등장행렬은 sparse하다는 단점이 있다. 벡터를 표현할 때 차원의 수가 너무 많아 sparse하고 벡터의 의미가 제대로 반영되지 않을 수 가 있다.
Word2Vec은 dense하고 의미를 어느정도 잘 반영한 벡터를 만들 수 있지만, window size를 기반으로 하여 전체 코퍼스의 정보를 담지는 못한다. Co-occurrence Matrix는 전체 코퍼스의 정보를 담을 수 있지만 벡터의 의미가 제대로 반영되지 않을 수 있고 너무 sparse하게 표현된다. 그렇다면 dense하게 벡터를 나타내고 전체 코퍼스의 정보를 담을 수 없을까? 그리하여 나온 기법이 Glove이다.
먼저 Co-occurrence Matrix의 벡터를 연산하기 위해서 동시등장 확률의 비율을 활용한다.

예를 들어, ice는 water와 유사성이 높기 때문에 확률이 높게 나오고 gas와는 유사성이 낮기 때문에 확률이 낮게 나온다. ice와 steam의 관계를 알기 위해 ice에 대한 확률과 steam에 대한 확률의 비율을 사용할 수 있다.
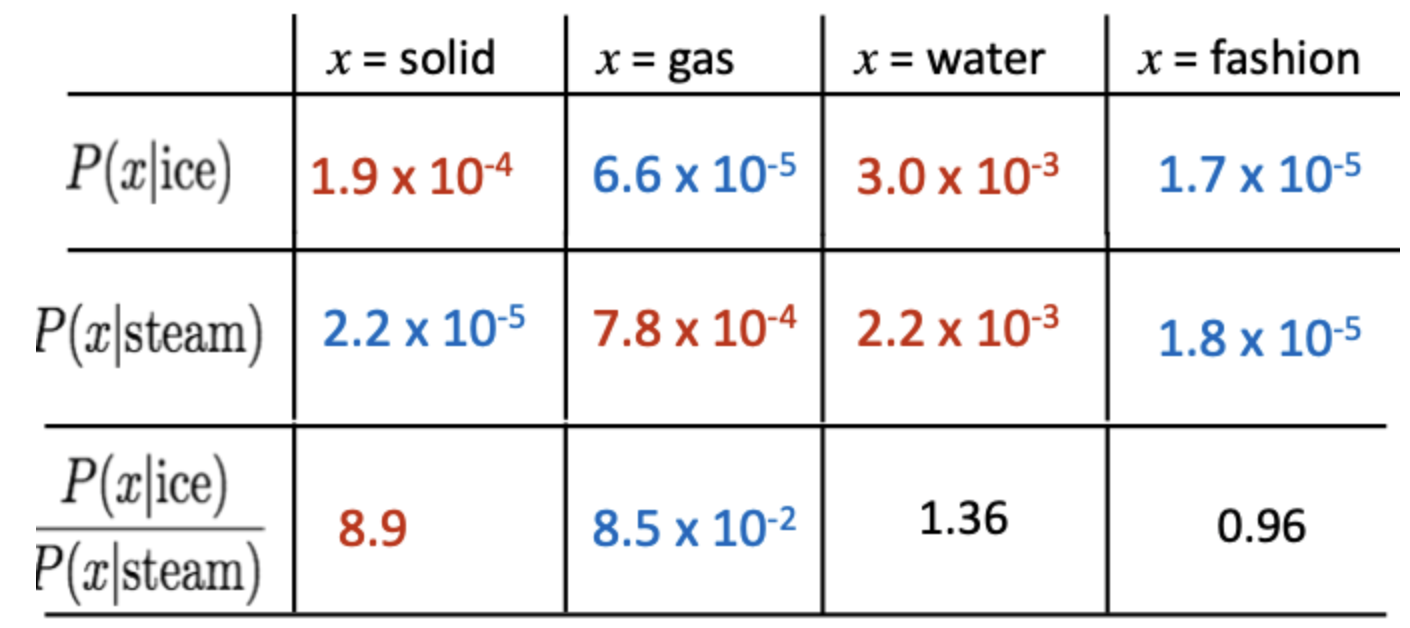
위와 같은 수치로 구성되어 있을때, ice가 등장했을 때 solid가 등장할 확률을 steam이 등장했을 때 solid가 등장할 확률로 나누었을 때 8.9라는 높은 수치가 나온다. 그러나 water와 fashion이라는 같이 등장할 확률이 높거나 같이 등장하지 않을 확률이 낮으면 1에 가까운 수치가 나온다.
벡터의 공간을 선형적으로 나타내기 위해 벡터의 내적을 통해 다음의 식을 정리한다.
이때 는 3가지 조건을 충족해야된다.
- center word는 context word로 등장할 수 있기 때문에 교환법칙이 성립해야함.
- 동시등장행렬 는 대칭행렬
- 준동형을 만족 ex)

하지만 가 0이 되면, 가 무한대로 발산하기 때문에 손실함수 에 weighting function을 함께 사용했다. 또한 빈도수가 낮은 단어와 빈도수가 너무 높은 단어에 대한 규제를 위하여 사용되었다.
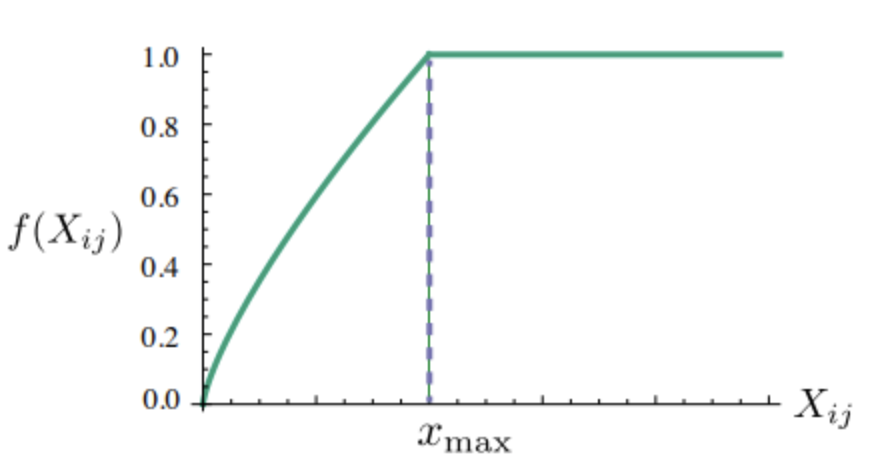
Glove의 목적함수는 다음과 같이 정리할 수 있다.