DA-Transformer: Distance-aware Transformer

0. Abstract

현재 NLP에서 Transformer기반의 language model이 좋은 성능을 보여주고 있다. ex) GPT, BERT,... 그러나 이러한 language model에 사용되는 위치 혹은 거리 embedding은 실제 거리 정보를 반영하지 않기 때문에 token간 거리를 capture하는데 최적이 아닐 수 있다. 따라서 본 논문에서는 token간 실제 거리를 반영하여 query와 key의 attention weight를 계산하여 re-scale 적용한다. 구체적으로, 다른 self-attention heads에서 query-key token 간 상대적인 거리들은 서로 다른 parameter로 계산되고 이러한 parameter들은 각 head가 long information,short information 사이에 선호도를 제어하는, 편협되지 않은 정보를 제공하기위해 제어하는 역할을 한다. Raw weight(self-attention은 상호 간 거리를 학습해야하니까 이 정보가학습되지 않은 weight들은 optimal하지 않다. 따라서 학습가능한 sigmoid function을 설계했고 그를 통해 적절한 range를 가질 수 있게 re-scale coefficient를 mapping했다. 본 연구에서는 raw self-attention weight를 clip하기 위해 ReLU 함수를 통해 음수를 제거하고 sparsity를 유지했고, self-attention 모듈에서 실제 거리를 encode하기 위해 re-scaled coefficient를 곱했다.

1. DA-Transformer

1.1 Head-wise Distance Weigthing

기존 Transformer와 input 형태는 비슷하지만 matrix안에 각 token의 representation token또한 포함되어있다.

$N$: Sequence length

본 연구에서 $i$번 째 token과 $j$번 째 token과의 real relative distance를 $R_{i,j}$, $R_{i,j} = |i-j|$라고 denote했다. 그리고 relative distance matrix $\mathbf{R} \in \mathbb{R}^{N \times N}$으로 정의할 수 있고 이는 모든 pair의 relative distance를 포함하고 있다, 이는 self attention matrix와 똑같은 shape.

각 head에서 학습 가능한 parameter인 $w_i$를 통해 relative distance matrix $\mathbf{R}$를 학습한다.

본 연구의 방법에서는 $\mathbf{R}$의 양수 value가 음수의 value보다 attention weight에 더 강하게 적용된다. 따라서 positive $w_i$는 attention head가 long-distance information을 더 선호하는 것을 의미하고, 반대로 음수의 $w_i$는 short-distance information을 선호하는 것을 의미한다. 각 다른 value의 $w_i$는 서로 다른 attention head가 서로 다른 preference를 가지고 있을 것이다.

3.2 Weighted Distance Mapping

Raw weighted distance는 attention weight에 적응하기에는 적절한 range가 아닐 수도 있기 때문에, 특정 함수를 통해 re-scaled coefficient를 적용해야 한다.

여기에는 5가지의 요구사항이 적용된다.

(1) $f(0)= 1$, zero distance(자기 자신 token과의 거리)
(2) $f(\hat{\mathbf{R}}^{(i)}) = -\infty = 0$, local 정보를 선호하는 head에서는 long range 정보에 대한 surpass가 적용되어야하기 때문.
(3) $f(\hat{\mathbf{R}}^{(i)}) = +\infty$ will be limted, 모델이 long sequence에 대해 정해진 길이에 대해서만 process해야한다.
(4) scale 함수 $f(\dot)$가 tunable 해야한다.
(5) scale 함수 $f(\dot)$가 monotone 해야한다.

위를 만족하기 위해 $\mathbf{R}$와 학습가능한 parameter $v_i$에 대해서 학습가능한 sigmoid 함수를 적용했다.

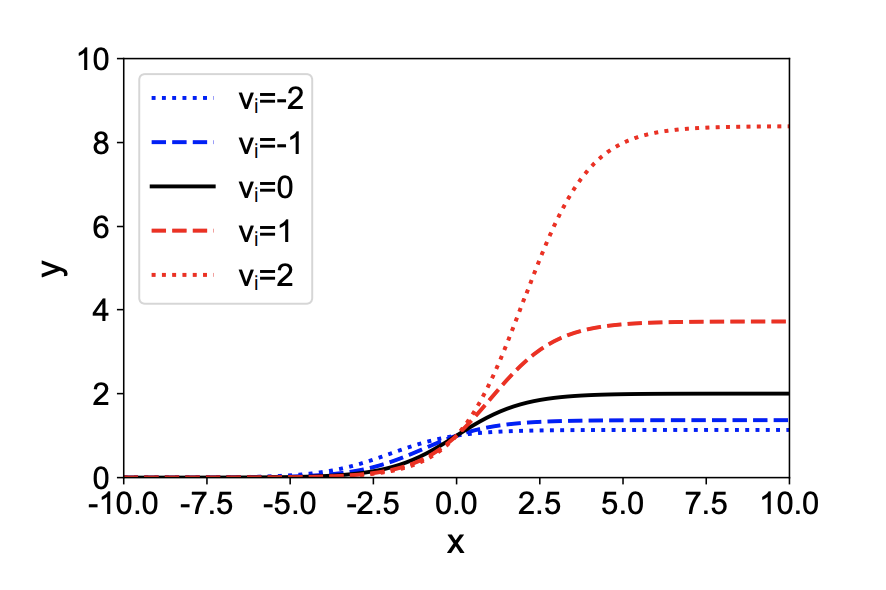
서로 다른 학습가능한 parameter $v_i$의 value를 통해 sigmoid function의 curve를 나타낸 plot이다. $v_i$의 값이 커질수록 curve의 upperbound가 커지는 것을 확인할 수 있다, 이 뜻은 distance의 information이 더 강하다는 것을 알 수 있다. $v_i = 0$일 때는 기존 simgoid 함수와 똑같은 형태를 보여주고 있다. 다음과 같은 함수를 통해 re-scaled coefficient를 얻을 수 있고 이를 몇가지 예시를 통해 plot을 그려봤다.

3.3 Attention Adjustment

이렇게 구한 re-scaled coefficient를 가지고 raw attention weight를 계산한다. 그러나 그대로 multiply하기에는 어려움이 있다. Token간 relation이 적고, re-scaled coefficient가 높을 때, final attention weight가 over amplified될 가능성이 있기 때문이다. 따라서 본 저자는 ReLU함수를 적용하여 non-negative를 유지하도록 했고 sparsity를 유지할 수 있도록 positive value만 sharp하게, 조금 극단적으로 계산했다고 볼 수 있다.