이상화 교수님의 KOCW 강의를 듣고 작성한 리뷰이다.
선형대수에서 다루는 주제는 행렬과 벡터를 바탕으로 하는데 행렬은 선형적 관계를 나타낸다.
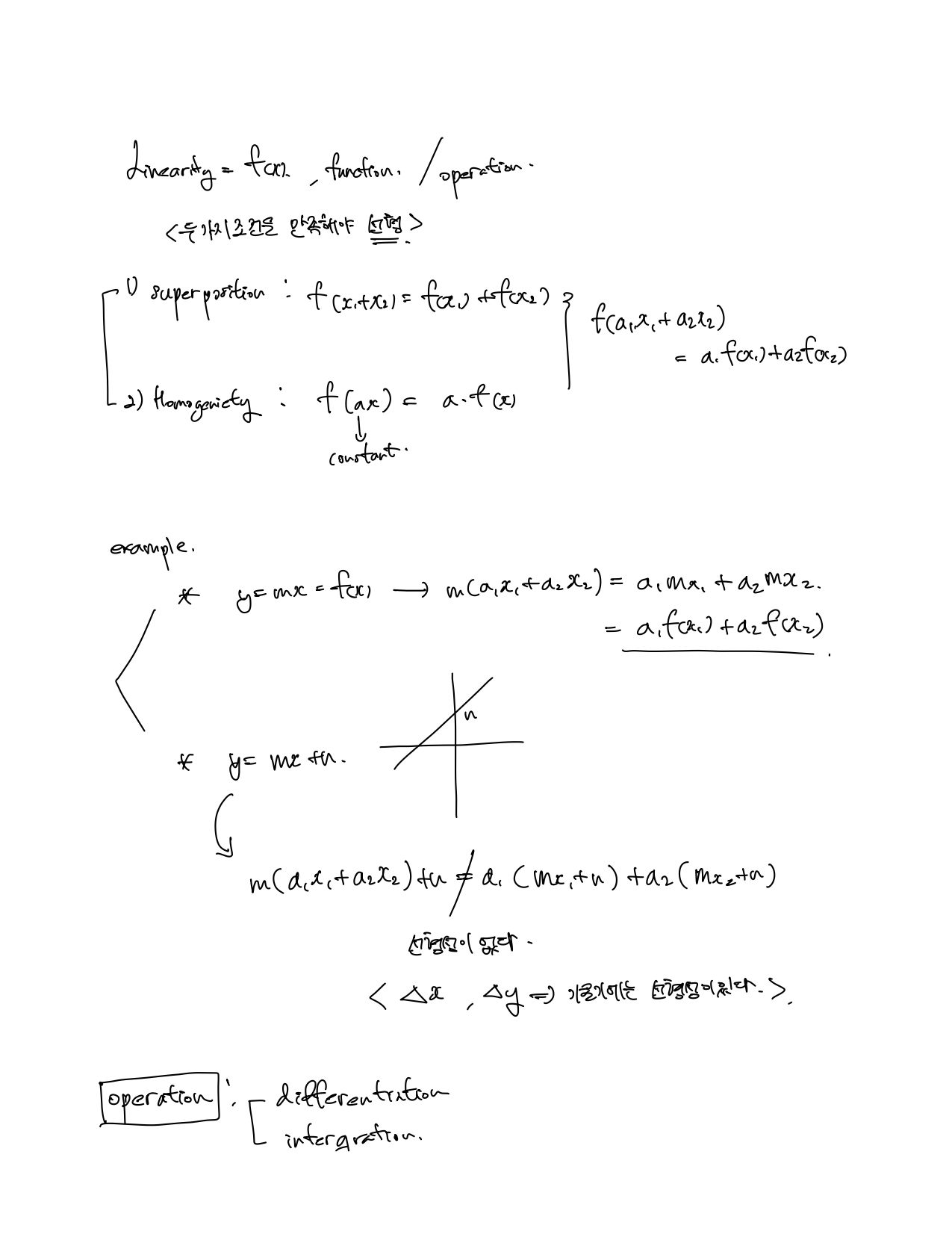
선형성이란 직선을 나타내는 것이 아니라 superposition과 homogeneity를 만족해야한다.
예를 들면, 어떠한 물체를 1의 힘으로 밀었을 때 1mm 이동하고 2의 힘으로 밀었을 때 2mm 이동한다면 2의 힘으로 밀고 1의 힘으로 밀면 2mm 이동하고 그 다음 1mm 이동해서 총 3mm를 이동할것으로 예상할 수 있는데 이것이 바로 superposition을 가지고 있기 때문이다.
다음 예를 들어, 1의 힘으로 1mm 이동시킬 수 있다면, 3의 힘으로는 3mm 이동시킬 수 있는것을 알 수 있는데 이것이 바로 homogeneity이다.
또한 differentiation과 integrationd을 했을때도 마찬가지로 선형성을 만족한다.
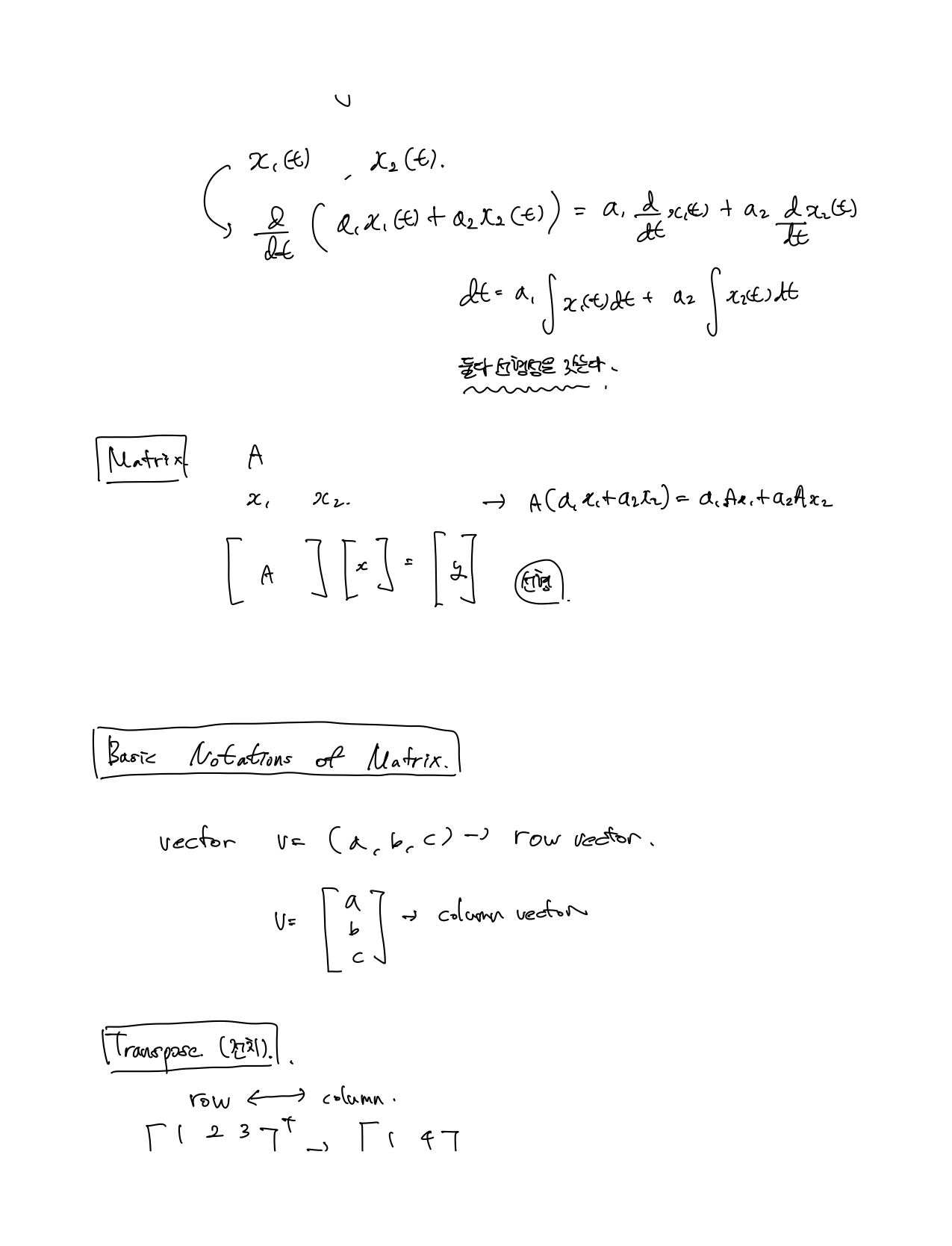
벡터는 보통 column vector를 가정한다.(feature가 column으로 구성되어 있어서 그런가? 잘모르겠다)

Linear Combination은 일차 결합과 같은 말이다. Linear combination은 vector들의 scalar배들이 합으로 새로운 조합의 vector를 얻는 연산을 뜻한다. Scalar-vector의 곱을 기하학적으로 생각해보면 vector의 길이를 늘리거나 줄이는것이고, 두 vector의 덧셈은 두 vector가 이루는 평행사변형의 대각선의 길이와 같다.

행렬은 교환법칙이 성립하지 않고 항등원이라는 개념이 있는것을 알았다.
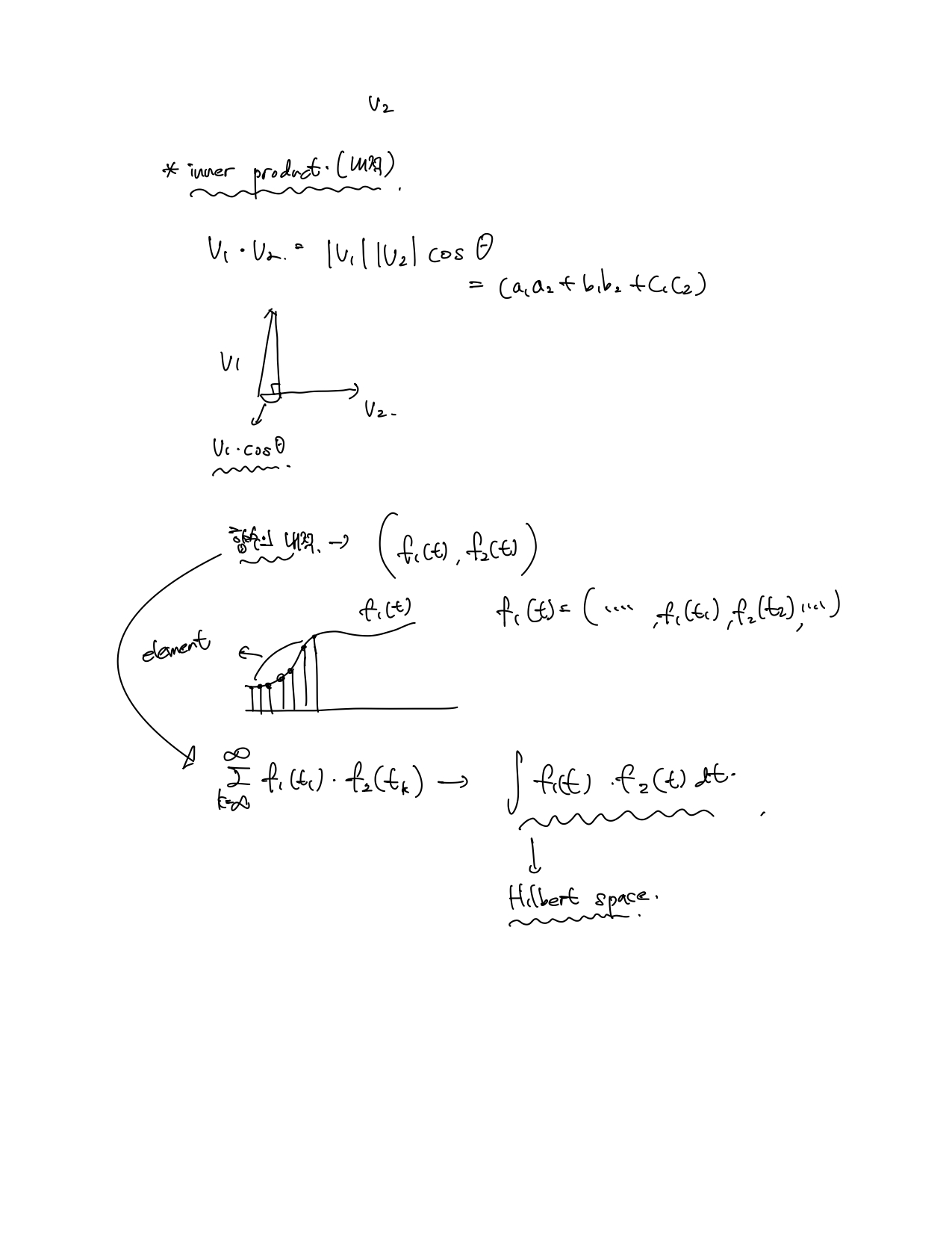
Vector의 내적(inner product)란 두 vector에서 하나의 vector가 다른 vector와 얼마나 유사한지 나타내주는 값이다. Cosine 유사도를 통해 두 vector 간의 cosine 각도를 구할 수 있는 유사도를 말한다.