Positional Encoding

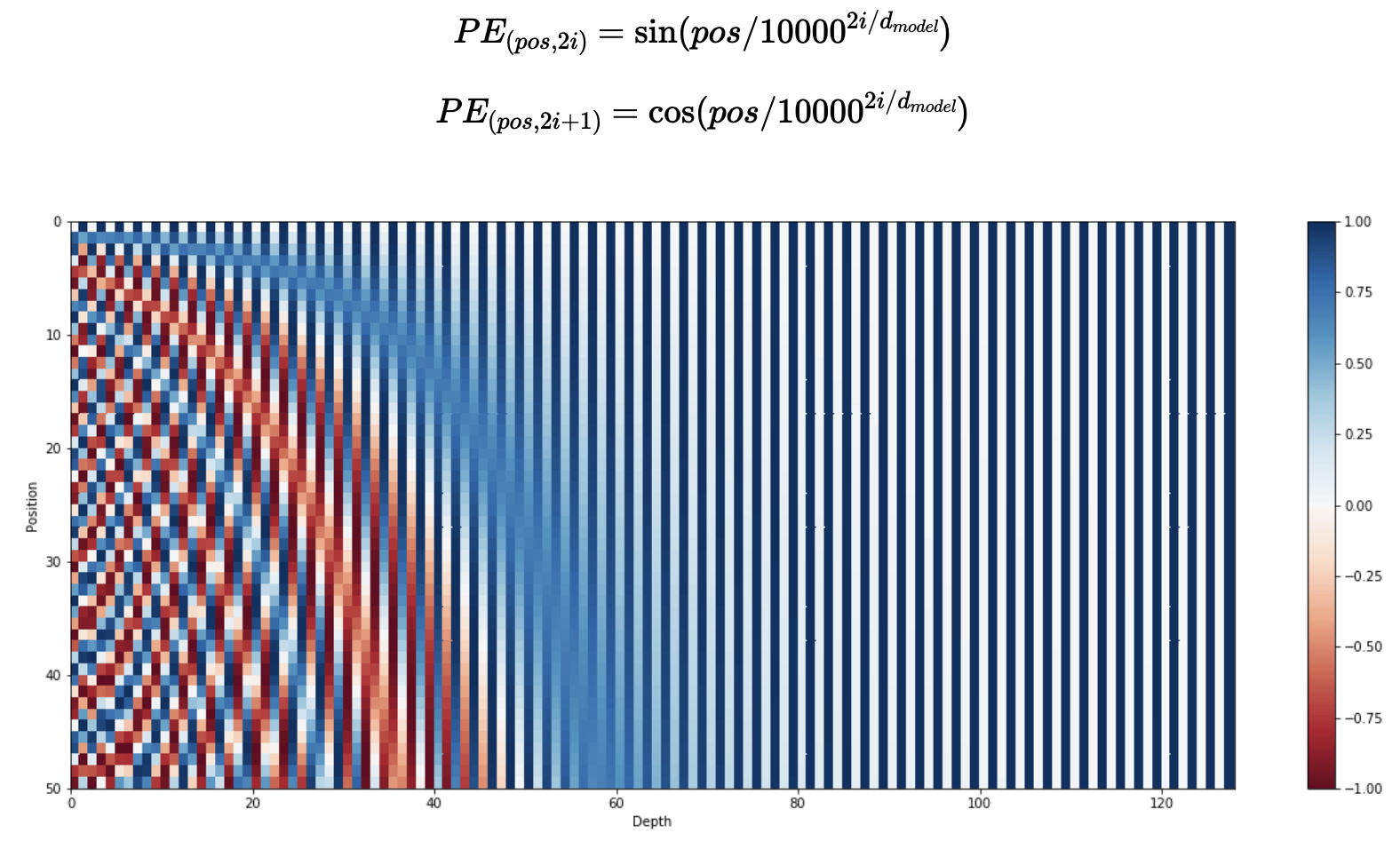
Introduction

Transformer 논문에서도 자세하게 설명되어있지 않고 가볍게 넘겼던 positional encoding에 대해 이해하지 못했던 부분을 더 공부해봤다. 자연어 처리에서 sequence의 위치는 어순을 뜻하며 어순은 언어를 이해하는데 꼭 필요한 정보이다. 그러나 Transformer는 input의 token이 RNN과는 다르게 parallel하게 처리되기 때문에 sequence 위치에 대한 정보가 없어 도입된 개념이다.

Positional Encoding

먼저 positional encoding이란, 입력된 sequence에서 token의 위치에 대한 representation을 의미한다. 예를 들어, sequence $X = [x_1, x_2, x_3, ... x_n]$이 입력되었을 때, positional encoding은 sequence $X$의 원소($x_1, x_2, ...$)의 위치와 위치에 대한 정보를 담고 있는 tensor가 된다. 이때 Transformer에서 input sequence의 embedding과 positional encoding 값이 더해지려면 같은 dimension을 가져야하므로 positional encoding은 [sequence length, embedding dimension]이 되어야한다.

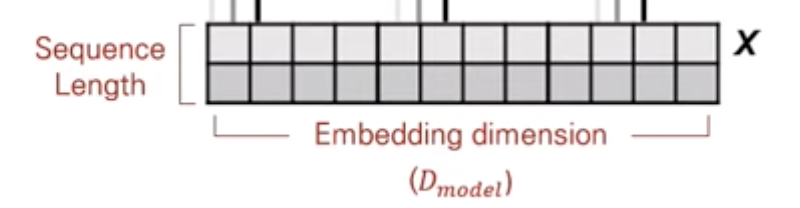
Positional Encoding을 위해서는 3가지 고려사항이 있다.

• 각 위치에 대한 유일한 벡터 값인지
• 다른 sequence length에도 적용할 수 있는지
• 다른 sequence length의 두 index간 거리가 일정한지

Method 1.

Positional Encoding의 가장 쉬운 방법으로는 아래 그림처럼 index별로 위치 값을 배정하는 방법이다.

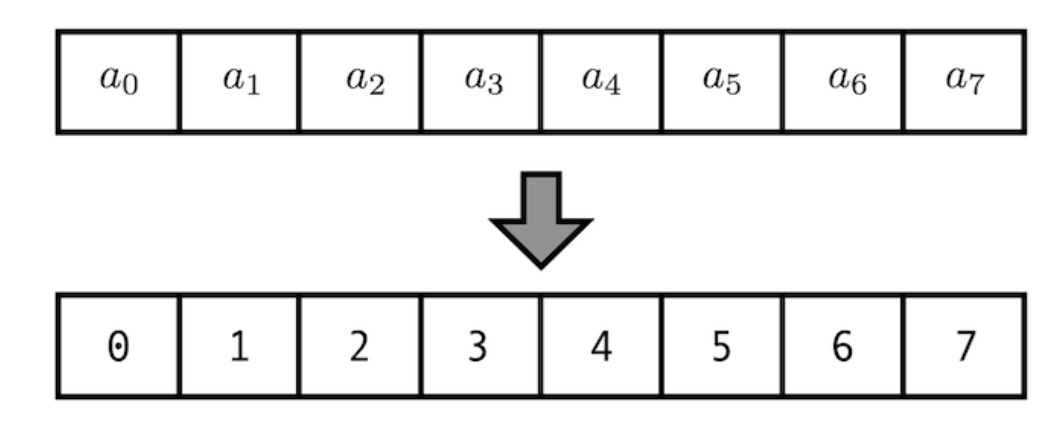
매우 간단하지만 이 method를 사용할경우, sequence의 length가 길어질경우 index값이 커질수록 positional encoding값도 커지게 되므로 gradient exploding이 일어나 정보가 손실된다.

Method 2.

다음 방법으로는 위 method 1의 값에 normalization을 적용한 방법이다.

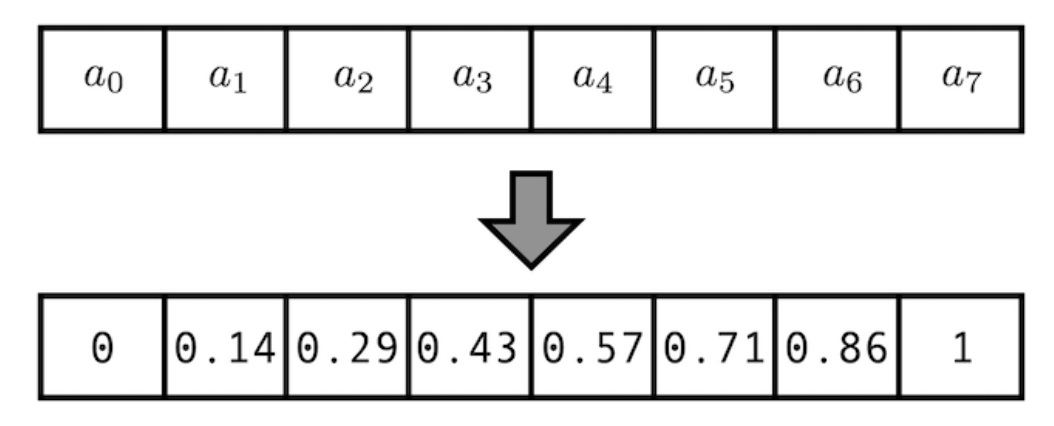
인덱스가 커짐에 따라 positional encoding 값이 커져 문제가 되기 때문에 index 최대값으로 나누어 모든 값을 0~1까지로 나타내는것인데, 이러한 방법은 sequence의 length에 따라 encoding 값이 달라지기 때문에 좋은 방법이 아니다. 예를 들어, sequence length의 길이가 20인 data에서 8번째 positional encoding 값과 10인 data의 4번째 positional encoding값이 동일하기 때문이다.

Method 3.

다음 방법은 method 1를 이진수로 표현한 방법이다.

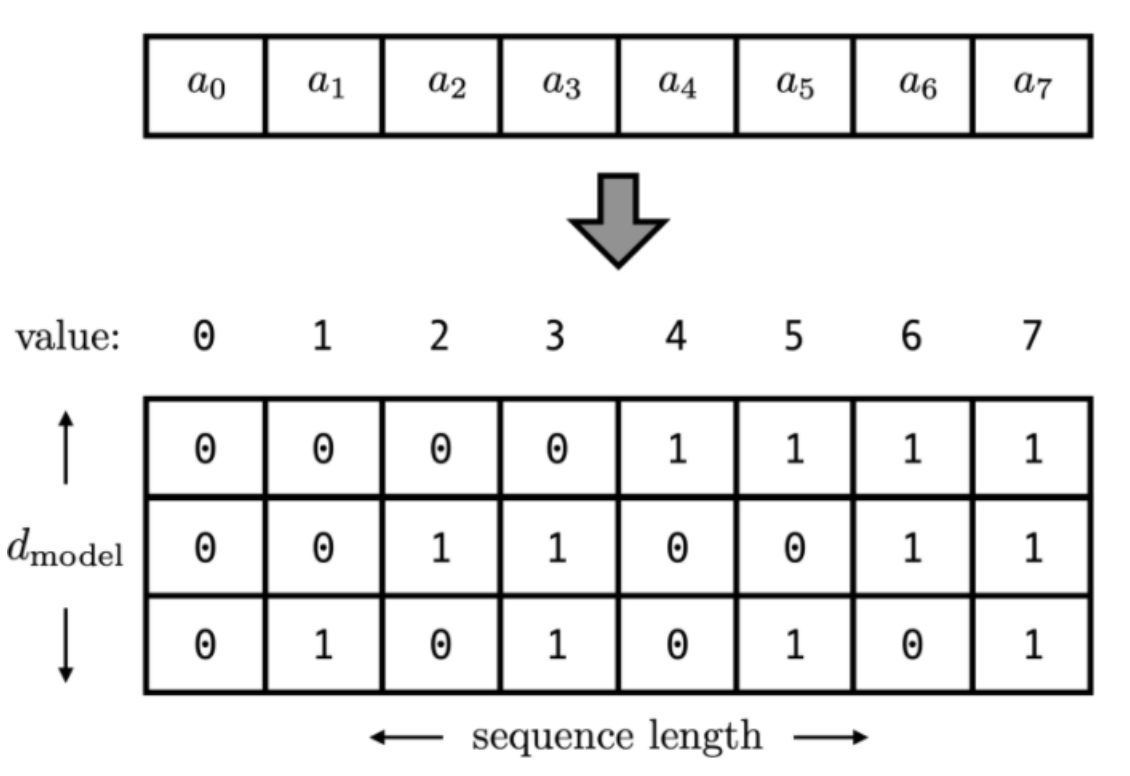
Method 1의 positional encoding 값을 이진수로 나타내고 positional encoding의 차원을 늘려 $d_{model}$값을 vector로 변환한다. 하지만 이러한 방법은 결국 연속적인 vector가 아닌 discrete한 vector값이 된다.

Continuous binary vector

Method 3에서 positional encoding값이 0과 1을 순환하며 변화하는것을 알 수 있다. 그러나 연속적인 vector로 나타내기 위해서는 0과 1을 순환할 수 있는 함수가 필요한데 그것이 바로 sine 함수이다. Sine 함수는 -1부터 1까지로 표현되기 때문에 정규화를 따로 할 필요가 없다.

예를 들어, 볼륨을 조절하는 dial이 있다고 생각할 때, dial은 0~1 사이를 계속해서 반복한다. 512 dimension의 볼륨을 조절하고 1개의 dial이 아닌 8개의 dial로 조절한다고 가정한다면 첫 번째 dial은 한칸, 두 번째 dial은 두칸, 세 번째 dial은 네칸을 움직인다면 모든 볼륨의 크기를 표현할 수 있다.

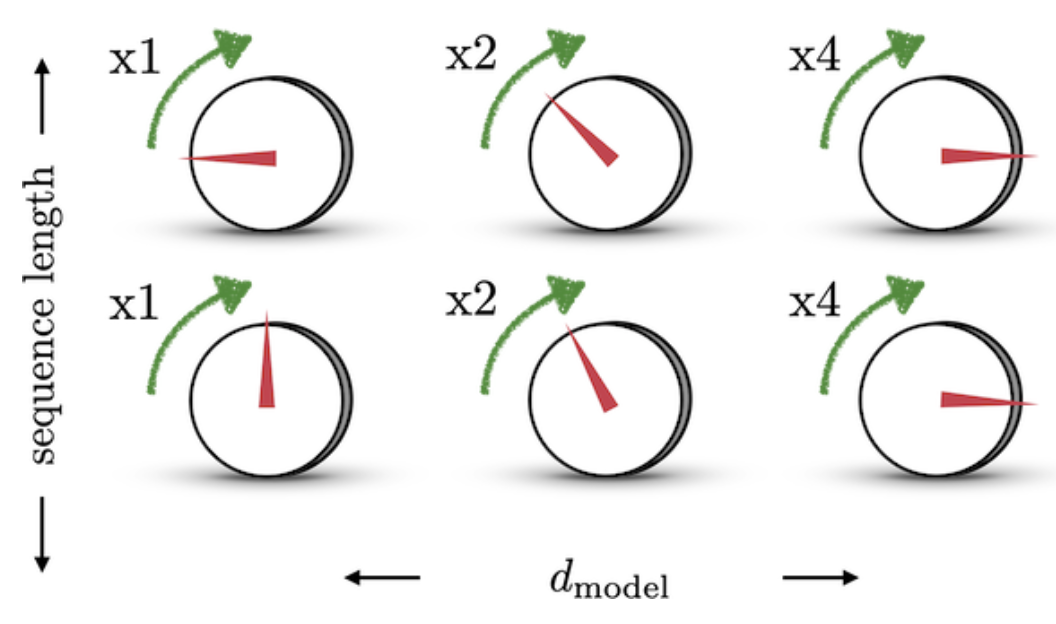
이러한 방법을 수학적으로 표현하면 첫 번째 dial (=$d_{model}$의 첫 번째 차원)은 sequence의 1 step을 진행할때마다 0과 1의 값이 바뀌니까 $\pi/2$가 주기가되고 두 번째 dial은 2 step을 진행할때마다 0과 1의 값이 바뀌어 주기가 $\pi/4$가 된다. 따라서 아래와 같은 식으로 positional encoding tensor를 정리할 수 있다.

$i$는 각 sequence의 index를 나타내고 $j$는 positional encoding의 dimension을 나타낸다.

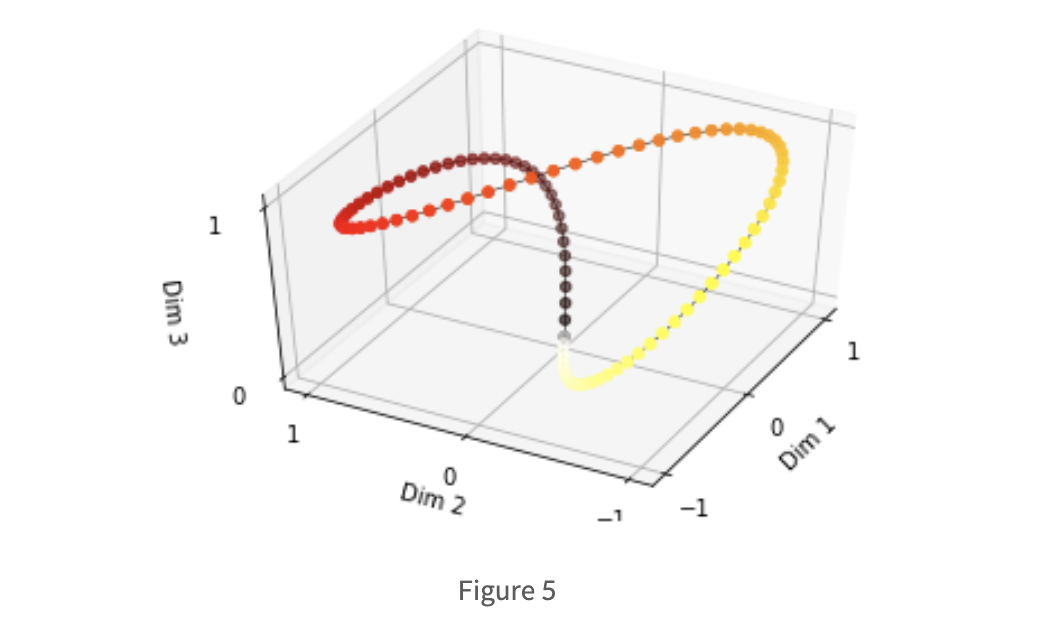
Dimension이 3일 때, 각 dim의 주기를 sin함수로 나타대면 위 그림과 같다. 각 dim의 주기가 $2^n\pi$이기 때문에 3차원 공간에서 닫힌것을 확인할 수 있다. 다른 위치에 존재하는 token의 positional encoding 값이 같아진다는 뜻으로 사용할 수 없다는 문제가 생긴다. 굳이 positional encoding의 vector값이 이진 vector일 필요는 없고, 각 index의 위치 값을 다르게 나타내면 되기 때문에 $j$에 따라서 주파수가 감소하면 된다. 즉 positional encoding값이 순환하지 않고 계속 증가하게 만드는것인데, 이를 표현하면 아래의 식과 같다.

다음 문제점은 $i$의 positional encoding vector가 $j$의 positional encoding vector로 표현되게 line transformation이 가능하게 해주는것이다. 이것은 self-attention layer에서 각 위치 별 다른 모든 위치에 있는 token들과 attention score를 계산한다는 점에서 필요한 요소이다. 예를 들어, 'I'm sorry about your friend'에서 'I'와 'friend'와의 attention score를 계산해야되는데 거리가 멀리 떨어져있다. 이때 positional encoding vector가 다른 index의 positional encoding vector의 선형변환으로 표현될 수 있으면 attention에서 조금 더 쉽게 위치 정보를 얻을 수 있을것이다.

Sine and Cosine

각 위치 별 positional encoding vector로 구성된 $PE$ matrix가 $v^i = [sin(w_0x_i), sin(w_1x_i), ... sin(w_{n-1}x_i)]$로 구성되어있으면 선형변환을 위해서는 아래와 같은 식을 만족해야한다.

위의 식을 만족하는 linear transformation $T(\nabla x)$를 찾을 수 있어야 한다. 이때 $x_i$가 sine 함수의 각도이기 때문에 cosine과 sine 함수의 각도를 rotation하는 회전변환행렬로 해결할 수 있다.

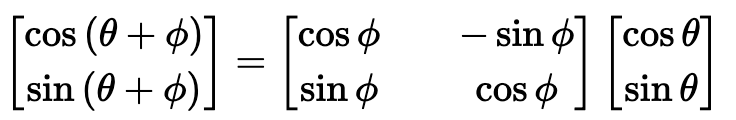
먼저 $v_i$에 대해 sine 함수 값을 cosine 함수 값으로 대체할 벡터를 구하고 $PE$행렬을 sine함수와 cosine 함수를 번갈아가면서 구성한다.

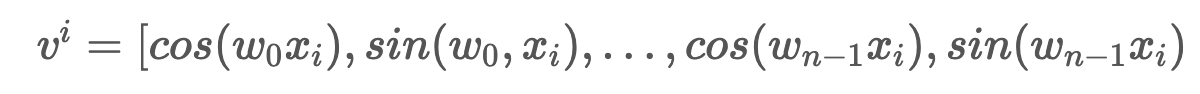
Cosine 함수와 sine 함수를 번갈아면서 사용함으로써 각 index 별 positonal encoding vector 간의 선형변환이 가능해진다.

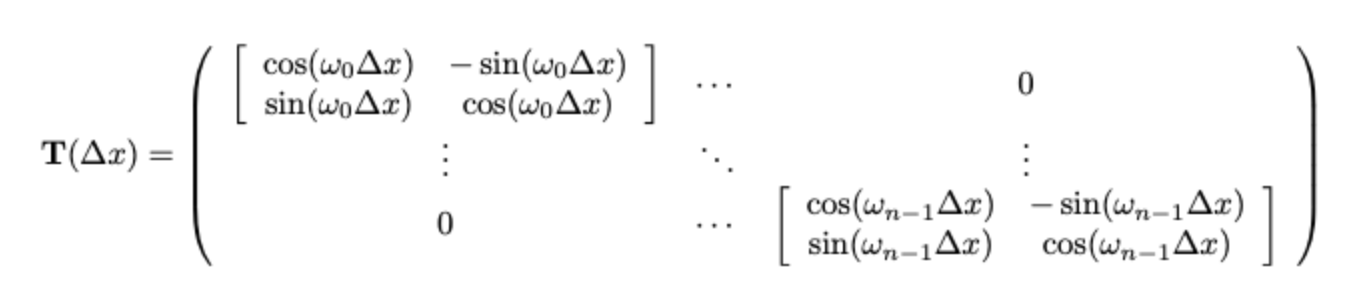
따라서 $PE$행렬의 각 행은 sine과 cosine 함수에서 각 위치별로 연결된 vector이다. 그리고 $PE$행렬의 행은 sine과 cosine 함수가 번갈아가면서 구성되고 열은 embedding dimension이 커지면서 주파수가 감소한다.