[LeetCode] DP 기본 문제들3- Knapsack Problem 활용 문제들; Partition Equal Subset Sum, Coin Change, LCS (JavaScript)

gitgitWi's TIL·2021년 2월 17일

DP JavaScript ProblemSolving knapsack problem leetcode

LeetCode도장깨기

목록 보기

6/6

Youtube 코드 없는 프로그래밍 DP 플레이리스트 따라서,
LeetCode DP 중상급 문제 풀이

해설과 코드를 보면 쉬운데.. 구현이 참..

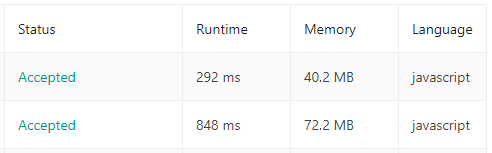
LeetCode 문제들 기준으로 2D Array 보다는 1D Array에서 runtime, memory 모두 성능이 좋다
특히 runtime은 많게는 2~3배까지도 차이가 난다
다만 구현하기에는 2D가 좀더 직관적이어서 편했다

일단 엑셀이나 손으로 2D Array를 그려보고,
그걸 바탕으로 점화식을 세워봐야겠다

Knapsack Problem 기본

LeetCode에는 응용 문제만 있어서,
GeeksForGeeks에 있는 0 - 1 Knapsack Problem 풀이
BOJ의 평범한 배낭

문제요약

총 무게한도가 정해진 배낭에 짐을 싣는 경우, 각 짐 value 합의 최대값
모든 경우의 수를 구하게 되면 짐 갯수가 조금만 많아져도 시간초과 에러 발생, 재귀로 하면 콜 스택 한도 초과 에러 발생
반드시 점화식을 구해서 풀어야 함
점화식 :

  특정 무게 한도 w에서 최대 value 
    = max(
      짐 a를 싣는 경우 w-a에서 최대 value + a의 value, 
      짐 a를 싣지 않는 경우 w-1에서 최대 value
     )

회고

역시나 점화식을 찾고 구현하는 데 어려웠던 문제
앞으로 응용 문제에서도 동일하게, 풀이 방법과 코드를 보면 쉬운데, 막상 풀려고 하면 잘 생각이 나지 않아 힘들었다
복습과 다수의 문제 풀이가 반드시 필요한 유형인 듯

점화식을 2D Array로 구현한 코드

/**
 * @param {number} W 가방의 최대 weight 한도
 * @param {number[]} wt 각 item별 weight
 * @param {number[]} val 각 item별 value
 * @param {number} N item 개수
 * @returns {number} 가방에 넣을 수 있는 최대 value
 */
function knapSack(W, wt, val, N) {
  // rows: 각 item을 넣을지 안넣을지 판단
  // cols: 현재 가방의 최대한도가 col이라면 얼마까지 넣을 수 있는지
  const memo = Array.from({ length: N + 1 }, () => Array(W + 1).fill(0));

  for (let n = 1; n < N + 1; n++) {
    for (let w = 1; w < W + 1; w++) {
      memo[n][w] =
        wt[n - 1] > w
          ? // 현재 item의 무게가 sub-problem 최대 한도보다 큰 경우
            // 이전까지 누적된 value 입력
            memo[n - 1][w]
          : // 현재 item 무게가 sub-problem 최대 한도보다 작은 경우
            // (현재 무게 빼고 누적된 value + 현재 value)와 (이전까지 누적된 value)와 비교
            Math.max(val[n - 1] + memo[n - 1][w - wt[n - 1]], memo[n - 1][w]);
    }
  }

  // 마지막 item까지 판단하고, 최대 weight 한도에서 가질 수 있는 최대 value
  return memo[N][W];
}

416. Partition Equal Subset Sum

문제요약

Subarray Sum과는 다름
Subarray는 배열에서 인덱스가 연속된 경우에 한해 구간합을 구하지만
Subset은 인덱스와 무관하게 부분합을 구하는 것
주어진 숫자 배열을 두개의 subset으로 나눌 때, 두 subset의 합이 같은지

회고

방식은 기본 Knapsack problem과 거의 동일
전체 problem에서 구하는 것과 sub-problem에서 구하는 것이 조금 달라질 수 있음
1D Array 풀이는 코드를 여러번 보고서야 이해할 수 있었다.. 수학적 사고(?)가 좀 있으면 점화식을 쉽게 세울 수 있을 것 같다

1D Array 활용

/**
 * @param {number[]} nums
 * @return {boolean}
 */
const canPartition = (nums) => {
  const sum = nums.reduce((a, b) => a + b, 0);

  if (sum % 2 !== 0) return false;

  const half = sum / 2;
  const dp = [];
  dp[0] = true;

  for (const num of nums) {
    for (let i = half; i >= num; --i) {
      dp[i] = dp[i] || dp[i - num];
    }
  }
  return dp[half] || false;
};

2D array 활용

/**
 * @param {number[]} nums
 * @return {boolean}
 */
const canPartition = (nums) => {
  const getSum = (arr) => arr.reduce((acc, val) => acc+val, 0);
  const totalSum = getSum(nums);
  if (totalSum % 2 === 1) return false;
  
  const halfSum = Math.floor(totalSum / 2);
  const SIZE = nums.length;
  
  const memo = Array.from({length: SIZE+1}, () => Array(halfSum+1).fill(false));
  memo[0][0] = true;
  
  for (let num = 1; num < SIZE+1; num++) {
    for (const sum in memo[num]) {
      if (sum === '0' || nums[num-1] === +sum) memo[num][sum] = true;
      if (nums[num-1] > +sum) memo[num][sum] = memo[num-1][sum];
      else memo[num][sum] = memo[num-1][sum] || memo[num-1][+sum-nums[num-1]];
    }
  }
  
  return memo[SIZE][halfSum];
};

518. Coin Change 2

문제요약

이전의 Coin Change가 동전을 단 한번만 쓸 수 있는 문제였다면,
이 문제는 동전을 무제한 사용 가능하다는 것
모든 조합을 구하게 되면 당연히 시간 초과 에러를 만날 수 밖에 없다

회고

앞의 부분합 문제와 거의 동일한 구조

1D array 활용

/**
 * @param {number} amount
 * @param {number[]} coins
 * @return {number}
 */
const change = function (amount, coins) {
  const memo = Array(amount + 1).fill(0);
  memo[0] = 1;
  for (const coin of coins) {
    for (let sum = coin; sum < amount + 1; sum++) {
      memo[sum] += memo[sum - coin];
    }
  }
  return memo[amount];
};

2D array 활용

/**
 * @param {number} amount
 * @param {number[]} coins
 * @return {number}
 */
const change = function (amount, coins) {
  const memo = Array.from({ length : coins.length + 1}, () => Array(amount + 1).fill(0));
  memo[0][0] = 1;
  for (const coin in memo)  {
    if (+coin === 0) continue;
    for (const sum in memo[coin]) {
      if (sum === "0") {
        memo[coin][sum] = 1; 
        continue;
      }

      memo[coin][sum] = (coins[+coin-1] > +sum)
        ? memo[+coin-1][sum]
        : memo[+coin-1][sum] + memo[coin][+sum - coins[+coin-1]];
    }
  }

  return memo[coins.length][amount];
};

1143. Longest Common Subsequence

문제요약

LCS로 유명한 문제
두 문자열에서 공통으로 포함되어 있으면서 순서가 바뀌지 않은 문자들의 개수
두 문자열 a, b의 가장 마지막 문자가 동일한 경우 이전까지 결과에 +1,
동일하지 않은 경우에는 a의 마지막 문자까지-b의 직전 문자까지 결과값과 a의 직전 문자까지 결과값-b의 마지막 문자까지 결과값 중 최대값을 입력

회고

1D Array로 푸는 경우에는 이전 값을 저장해서 활용하는 과정이 반드시 필요함
발상이 어려워서 산으로 가다가 결국 discuss 보고 해결..
코드가 이상해지면 발상이 잘못된 게 아닐까 돌아보게 되었다

1D Array(O(min(M,N))) 풀이

/**
 * @param {string} text1
 * @param {string} text2
 * @return {number}
 */
const longestCommonSubsequence = (text1, text2) => {
  if (text1 === text2) return text1.length;

  const s1 = text1.length;
  const s2 = text2.length;

  if (s1 < s2) return longestCommonSubsequence(text2, text1);

  const memo = Array(s2 + 1).fill(0);

  for (let i = 1; i < s1 + 1; i++) {
    let prev = memo[0];
    for (let j = 1; j < s2 + 1; j++) {
      let tmp = memo[j];
      if (text1[i - 1] === text2[j - 1]) memo[j] = prev + 1;
      else if (memo[j - 1] > memo[j]) memo[j] = memo[j - 1];
      prev = tmp;
    }
  }

  return memo[s2];
};

2D Array(O(MN)) 풀이

/**
 * @param {string} text1
 * @param {string} text2
 * @return {number}
 */
const longestCommonSubsequence = (text1, text2) => {
  if (text1 === text2) return text1.length;

  const s1 = text1.length;
  const s2 = text2.length;

  const memo = Array.from({ length: s1 + 1 }, () => Array(s2 + 1).fill(0));

  for (let i = 0; i < s1; i++) {
    for (let j = 0; j < s2; j++) {
      memo[i + 1][j + 1] =
        text1[i] === text2[j]
          ? memo[i][j] + 1
          : Math.max(memo[i + 1][j], memo[i][j + 1]);
    }
  }

  return memo[s1][s2];
};