From Perceptron to Neural Network

Figure: Example of Nerual Link

Perceptron

Velog equation sucks here...

B here stands for Bias. The bigger it is, the easier the equation($b + w_1x_1 + w_2x_2$) results 1.

Following is the figure of perceptron with specified Bias.

그럼 [식3.1]을 더 간결한 형태로 다시 작성해보죠. 이를 위해서 조건 분기의 동작(0을 넘으면 1을 출력하고 그렇지 않으면 0응ㄹ 출력)을 하나의 함수로 나타냅니다. 이 합수를 h(x)라 하면 식 [3.1]을 다음과 같이 표현할 수 있습니다.

Activate Function

It is the function decides whether to activate the perceptron or not. The function h(x) above is the one.

Let's take a look at the following equation.

This can be seperate into two parts.

$a= \text{Sum value of input signal and the bias}$
$y=\text{Result of activate function h}$

Figure: Perceptron with the appearnce of Activation Function

The single big circle on the right is a node, which is also called neuron.

Sigmoid function as an Activation function

Following equation is, of course, the sigmoid function. This can be used for activation function.

Implementing Step Function

Step function can be easily materialized like this.

import numpy as np

def step_function(x):
    y = x > 0
    return y.astype(int)

print(step_function(np.array([-1.0, 1.0, 2.0])))

Now let's see the graph of the step function.

x = np.arange(-5.0, 5.0, 0.1) # generates a numpy array range from -5.0 <= elem < 5.0 by the step of 0.1
y = step_function(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1) # set the range of axis y
plt.show()

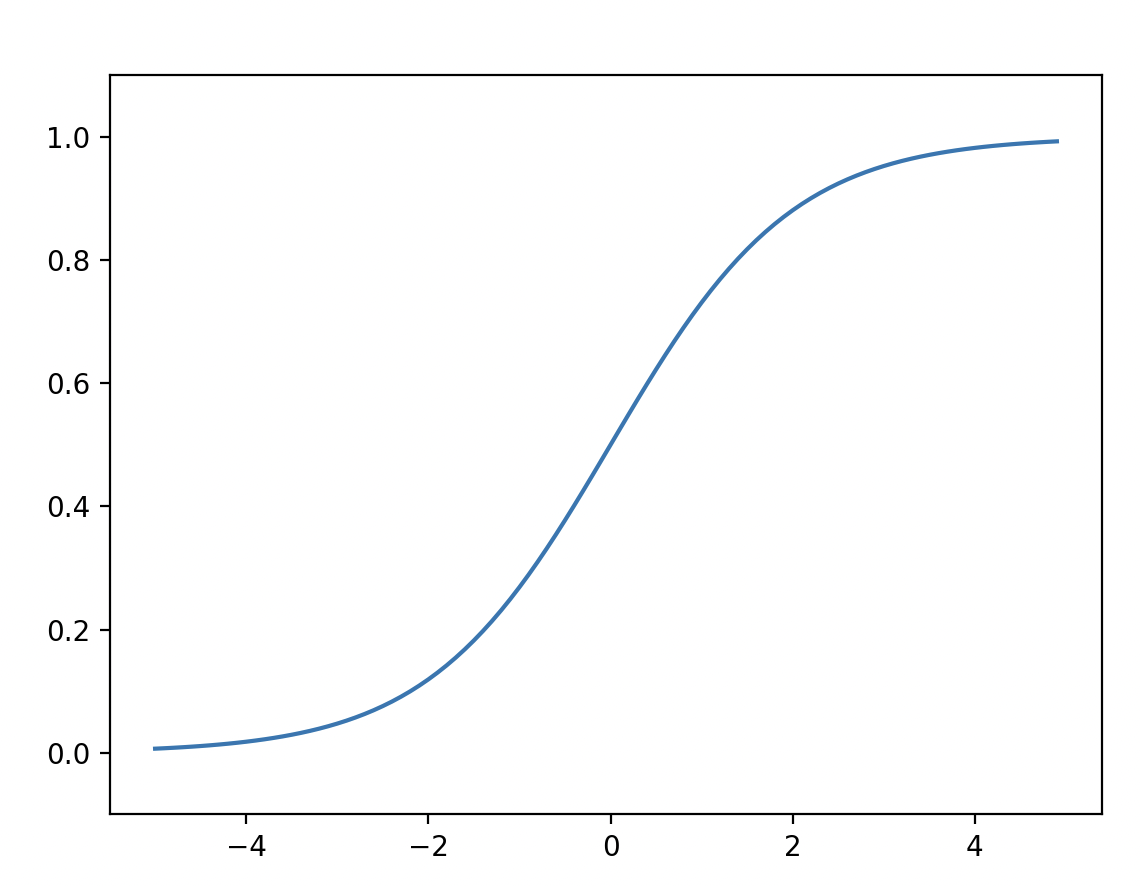
Sigmoid on python

def sigmoid(x):
    return 1 / (x+np.exp(-x))

Figure: Graphp of sigmoid function

Step V Sigmoid

	Step	Sigmoid
Graph
y	0 or 1	float-point numbers
commons	Both results the smaller value if the input value becomes less.	'''