[DL] 경사하강법

기울기: 모든 변수의 편미분을 벡터로 정리한 것

수치미분 구하는 함수

def numerical_diff(f, x):
    h = 1e-4
    return (f(x+h) - f(x-h))/(2*h)

문제1. $x_0=3,\ x_1=4$일때 $x_0$에 대한 편미분 $\frac{\partial f}{\partial x_0}$를 구하라

>>> def function_tmp1(x0):
...     return x0 * x0 + 4.0**2.0
... 
>>> numerical_diff(function_tmp1, 3.0)
6.00000000000378

문제2. $x_0=3,\ x_1=4$일때 $x_1$에 대한 편미분 $\frac{\partial f}{\partial x_1}$를 구하라

>>> def function_tmp2(x1):
...     return 3.0**2.0 + x1*x1
...
>>> numerical_diff(function_tmp2, 4.0)
7.999999999999119

이처럼 편미분은 변수가 하나인 미분과 마찬가지로 특정 장소의 기울기를 구합니다. 단, 여러 변수 중 목표 변수 하나에 초점을 맞추고 다른 변수는 값을 고정합니다. 앞의 예에서는 목표 변수를 제외한 나머지를 특정 값에 고정하기 위해서 새로운 함수를 정의했지요. 그리고 그 새로 정의한 함수에 대해 그동안 사용한 수치 미분 함수를 적용하여 편미분을 구한 것입니다.

이것을 하나의 함수로 만든 형태

def numerical_gradient(f, x): # 설명변수 x들이 주어졌을 때 함수의 기울기
    h = 1e-4 
    grad = np.zeros_like(x)
    
    for idx in range(x.size): # 앞의 예에서 tmp1, tmp2 함수 따로 정의했던 거 이렇게 정리.
        tmp_val = x[idx] # idx번째 x에 대입한 값을 저장.
        # f(x+h)
        x[idx] = tmp_val + h 
        fxh1 = f(x) # 수치미분을 위한 y값 계산.
        
        # f(x-h)
        x[idx] = tmp_val -h
        fxh2 = f(x) # 수치미분을 위한 y값 계산 (2)
        
        grad[idx] = (fxh1 - fxh2)/(2*h)
        x[idx] = tmp_val # 다른 설명변수들에 대한 편미분을 위한 값 복구.
	return grad

이 함수를 통해 편미분 결과를 얻을 수 있다.

>>> numerical_gradient(function_2, np.array([3.0, 4.0]))
array([6., 8.])
>>> numerical_gradient(function_2, np.array([0.0, 2.0]))
array([0., 4.])
>>> numerical_gradient(function_2, np.array([3.0, 0.0]))
array([6., 0.])

이 결과는 결국 크기가 2인 행렬(벡터)이며, 각 점에 대한 편미분 값을 수치미분 방식으로 구한 것이다.

이처럼 각 점에서의 기울기를 계산할 수 있다. ... 그런데 이 기울기라는 게 의미하는 건 뭘까요? 그림으로 그려보면 이해가 될 겁니다. 다만, 여기에서는 기울기의 결과에 마이너스를 붙인 벡터를 그려보겠습니다. ... 깅루기 그림은 방향을 가진 벡터(=화살표)로 그려집니다. 이 그림을 보면 기울기는 함수의 '가장 낮은 장소(최솟값)'를 가리키는 것 같습니다. 마치 나치만처럼 화살표들은 한 점을 향하고 있지요. 또 '가장 낮은 곳'에서 멀어질수록 화살표의 크기가 커짐을 알 수 있습니다.

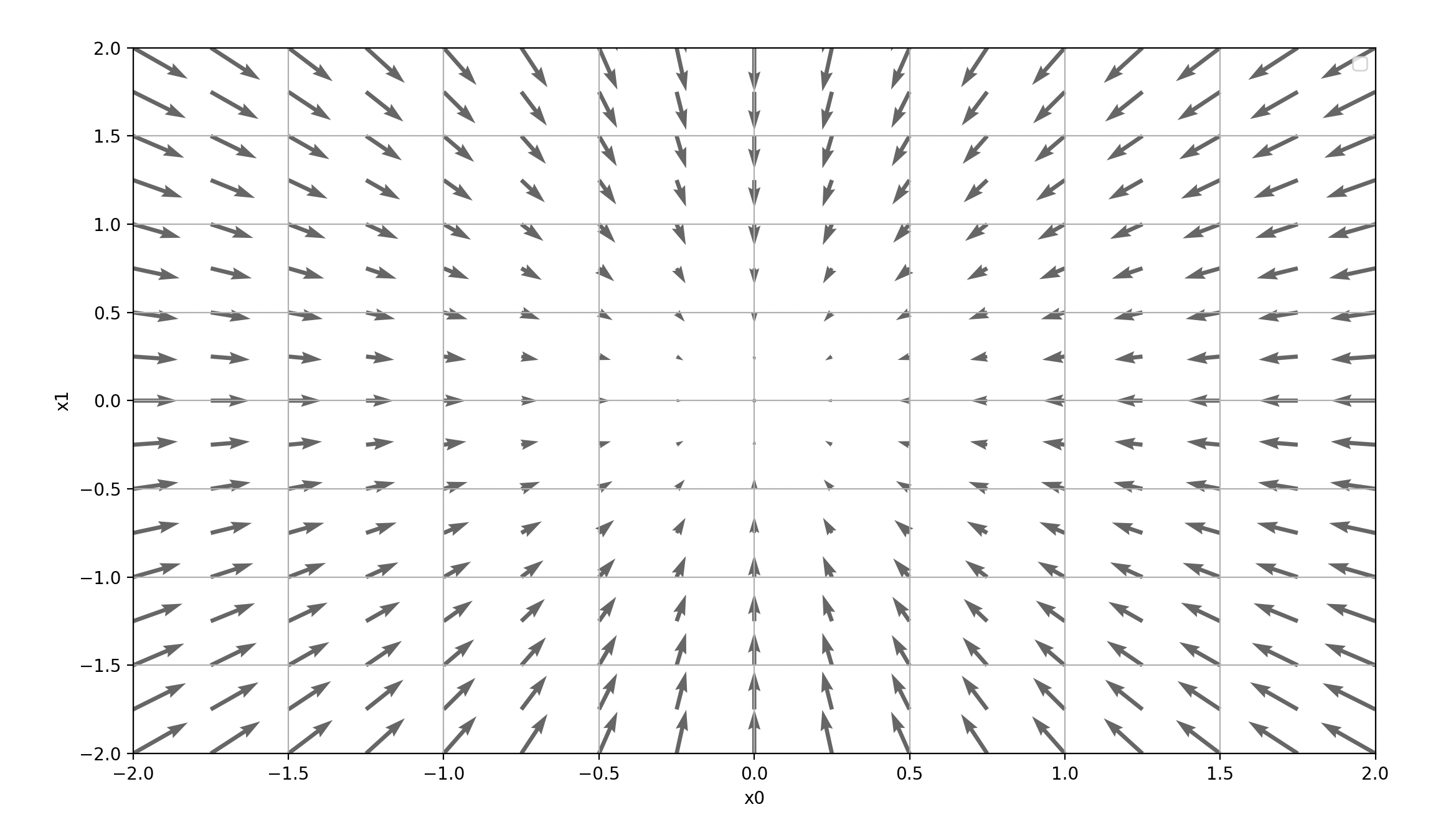
(함수가 두 변수를 각각 제곱한 형태기 때문에, 절대값이 가장 작은 지점으로 기울기 벡터가 그려진다)

드디어 경사법이 등장할 차례입니다. 경사법은 현 위치에서 기울어진 방향(편미분 값의 부호)으로 일정 거리만큼($\eta$) 이동합니다. 그런 다음 이동한 곳에서도 마찬가지로 기울기를 구하고, 또 그 기울어진 방향으로 나아가기를 반복합니다. 이렇게 해서 함수의 값을 점차 줄이는 것이 경사법입니다.

Note: 편미분 값은 편미분한 변수 x의 값에 비례한다.

따라서, 편미분 값이 양수라면, x 값을 그 부호의 에타 가중치 만큼 곱하여 역으로 빼주면, 기울기 값을 가장 작게 만드는 x값을 구할 수 있다.

Q.그럼 결국 편미분 값은 방향을 지시하는 거지? 그 절대적인 크기는 미비하고.
A. 네, 정확합니다! 편미분 값은 주로 방향을 지시하는 역할을 합니다. 경사 하강법(Gradient Descent)이나 최적화 과정에서 편미분 값의 절대적인 크기는 상대적으로 덜 중요하며, 이동 방향과 상대적인 변화 정도를 결정하는 데 사용됩니다.