[논문 리뷰 및 구현] Attention is all you need

pyross·2024년 6월 24일

paper

목록 보기

4/63

Abstraction

최근의 성능 좋은 sequence 변환 모델은 encoder, decoder 구조를 포함하는 RNN이나 CNN에 기반을 두고 있다.
가장 좋은 성능을 내는 모델도 attention 방식을 이용해서 encoder와 decoder를 연결하는 구조이다.
이 논문에서는 Transformer 즉 attention만 이용하는 모델을 제시한다.
transformer 모델은 매우 적은 학습 cost로 번역 작업에서의 우위를 보여준다.

attentioin mechanism이란?
rnn에서 등장한 방법

이미지 출처 wikidocs
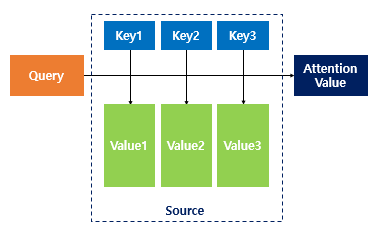
query를 각각 key와의 유사도를 dot product를 이용해서 구하고(dot product 시에는 값이 유사도를 반영한다. -> cosine similarity) 이를 value에 매핑을 한 후 더해서 attention value를 구하는 방법
이를 통해 query와 key의 유사도를 반영한 value 값을 얻을 수 있다.

1. Instroduction

RNN이나 LSTM과 같은 모델은 input, output을 하나씩 쪼개서 symbol을 계산하는 식으로 진행이 된다.
이 과정에서 hidden state $h_{t}$ 를 계산하기 위해서는 이전의 결과 값 $h_{t-1}$ 과 position $t$ 에서의 input이 필요하다. 이러한 순차적인 계산의 특성 때문에 RNN과 LSTM은 병렬처리가 불가능하다. 이는 sequence가 길어질수록 문제가 되는데 왜냐하면 메모리 제한으로 batch 처리가 힘들어지기 때문이다. 최근에 factorization trick, conditional computation 등으로 계산 효율성을 늘렸지만 여전히 근본적인 병렬처리의 문제점은 남아있다.
attention mechanism은 다양한 작업에서 input output 사이의 거리에 상관없이 강렬한 효과를 보였지만 recurrent network에서만 사용이 되고있다.
transformer는 recurrent를 사용하지 않고 attention mechanism을 활용하여 input과 output 사이의 관련성을 이끌어내고 병렬적인 연산을 가능하게 하여서 번역의 새로운 SOTA기술을 제시한다.

2. Background

ByteNet, ConvS2S과 같이 cnn을 base로 사용하여 hidden state를 병렬적으로 계산을 하려는 시도는 존재했었다. 그러나 이러한 모델들은 sequence의 거리가 멀수록 ConvS2S는 linear, ByteNet은 log로 계산량이 증가한다.
이러한 특성은 다른 위치의 dependency를 계산하는 것을 어렵게 만든다. transformer는 이러한 계산량을 상수로 줄여서 dependency를 계산하는 것에 특화가 되어있다. 그러나 이는 attention 가중치를 평균화 하기에 해상도가 줄어드는 문제점이 생기지만 이를 muti-head-attention으로 대응할 수 있었다.

3. Model Architecture

우선 encoder-decoder 구조를 알아야 한다.
최근 성능이 좋은 문장변환(번역 등) 모델은 encoder-decoder 구조를 가지는데 이는 다음과 같다.

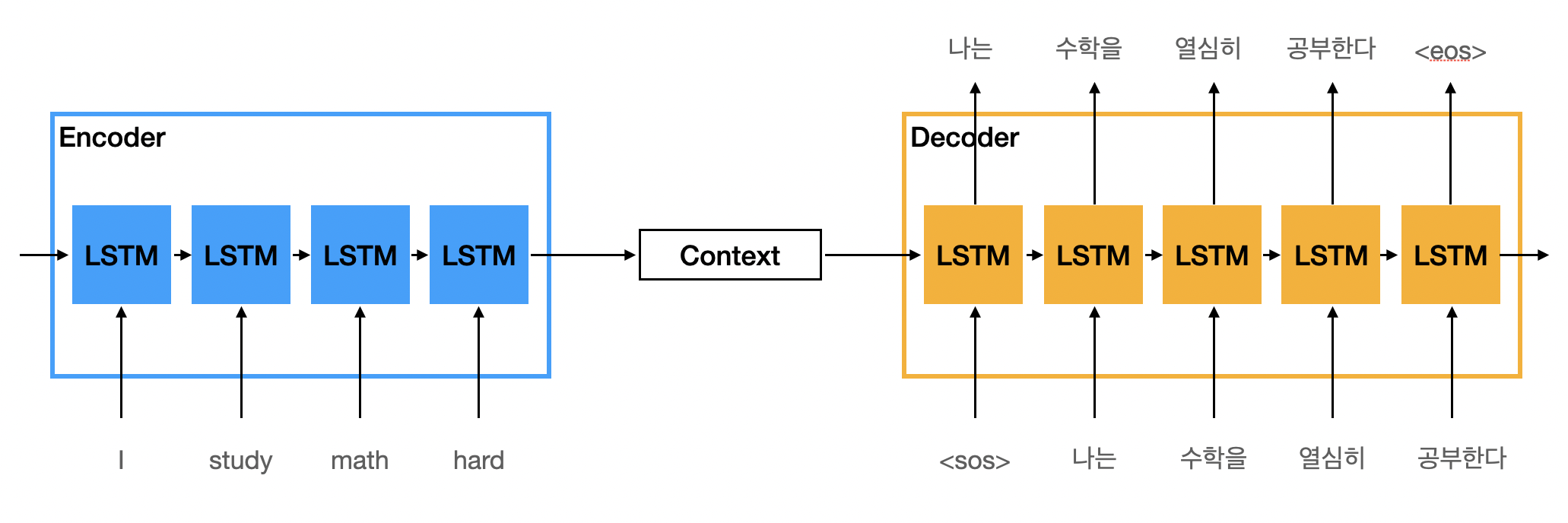
사진 출처
위 이미지는 LSTM을 이용한 encoder - decoder 구조인데 주어진 문장 I study math hard를 endoer를 이용하여 특정한 context vector로 압축한다. 그리고 이 내용을 토대로 decoder에서 context vector + 이전의 input을 받아서 한국어로 번역을 하는 모습이다.
여기에서 auto regressive도 알 수 있는데 auto regressive는 decoder에서 이전 자신의 입력을 다시 받아서 출력을 만드는 것을 뜻한다.

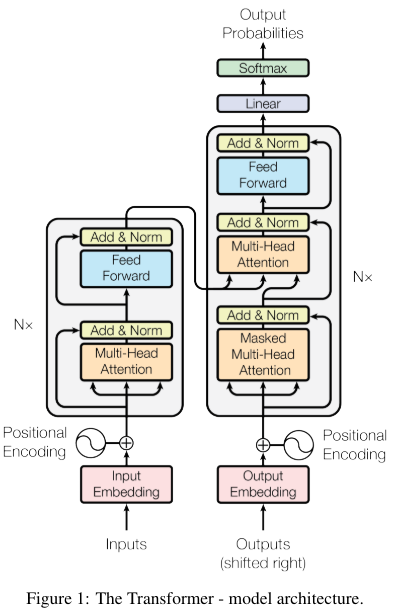
그리고 아래는 transformer의 encoder-decoder 구조이다.

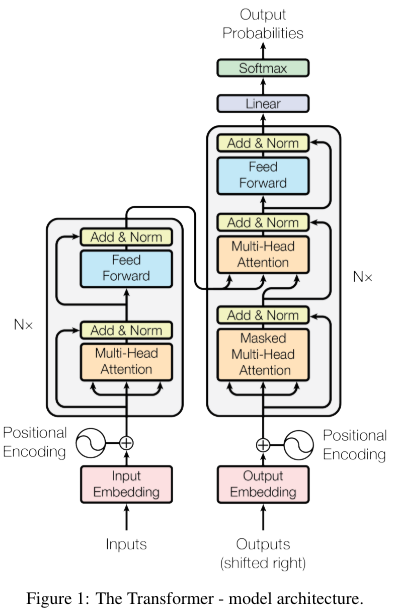
왼쪽이 encoder 부분이고 오른쪽이 decoder 부분이다.

3.1 Encoder and Decoder Stacks

Ecoder: encoder은 N=6의 동일한 layer로 구성이 되어있으며 각각 layer는 2개의 하위 layer를 가진다. 각각 multi head attention과 feed forward network이다.
그리고 각각 sublayer에 residual connection을 추가하고 다음 normalization을 수행한다.
결국 다음과 같이 수식으로 표현이 가능하다.
LayerNorm(x + Sublayer(x))
residual connection을 위해 $d_{\text {model }}=512$ 으로 설정하였다.
Decoder: decoder 역시 N=6의 동일한 layer로 구성이 되며 decoder은 encoder의 2 sublayer에서 추가로 1개의 multihead attention layer가 더 추가가 되었다. 이는 encoder의 output에 attention을 적용하기 위함이다.

추후에 나올 query-key-value에서 encoder의 값을 부분적으로 사용함으로써 attention을 적용한다.

또한 decoder에서는 self-attention layer를 수정해서 뒤에 나오는 위치를 참고하지 못하도록 수정했다. 즉 위치 i를 예측할 때 i보다 뒤에 값을 참고하지 않고 i보다 작은 위치만 참고하도록 하였음.

우리는 문장 번역을 할 때 주어진 input을 전체를 보고 결과 단어를 하나씩 보면서 번역을 한다. 이를 위해 encoder 결과를 전부 참고하여서 decoder에서는 encoder의 context vector 전부와 이전 출력을 참고하여서 출력을 하나씩 만들어간다.

3.2 attention

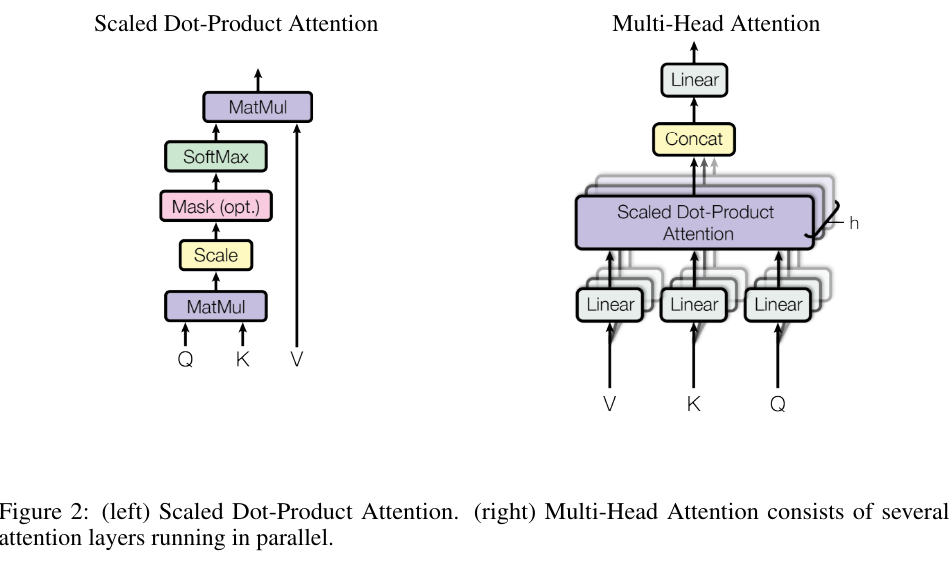
이전 attention에 대한 설명과 같이 Query와 Key를 MatMul을 해서 Query와 Key 사이의 유사도를 계산하고 이를 Softmax를 통해 비율로 변경한 후 V와 곱해 V에 관련성을 할당해주는 과정이다.
Multi head attention은 이러한 연산을 여러개를 붙여서 진행함으로써 여러명의 독자가 각각 할당받아서 유사도를 계산하는 것과 비슷한 효과를 낼 수 있다.

3.2.1 scaled dot-product attention

$\operatorname{Attention}(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V$ 이러한 공식으로 진행이 되고 $d_{k}$ 는 key와 query의 dim이다.
$d_{k}$ 를 나눠주는 이유는 $d_{k}$ 가 작을 경우 additive attention과 비슷하지만 $d_{k}$ 가 클 경우 additive attention이 dot-product attention보다 훨씬 좋은 경과를 내기 때문이고 이는 곱셈 과정에서 $d_{k}$ 가 크게 된다면 결과 값이 매우 커지고 softmax에서 gradient를 작게 만들기 때문이다.

3.2.2 multi-head attention

$d_{model}$ 의 차원에서 query, key, value를 1번 실행하는 것보다

위 그림과 같이 각각 주어진 Q, K ,V를 각각 다르게 학습된 linear projection을 h번 진행하고 이에 대해서 각각 병렬적으로 attention을 진행하는 것이 더욱 좋다는 것일 발견하였다.
그렇게 나온 attention output을 concat하고 다시 linear projection을 진행하는 것으로 final value가 완성된다.
이는 모델이 input에서 각각 다른 관점에서 다양한 시각으로 연관성을 분석할 수 있게 해줌으로써 성능을 올릴 수 있다.
이는 다음과 같이 수식으로 표현된다.
$\begin{array}{l} \text { MultiHead }(Q, K, V)=\text { Concat }\left(\text { head }_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head }_{\mathrm{i}}=\operatorname{Attention}\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \\ \end{array}$
각각 dim은 다음과 같다.
$W_{i}^{Q} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{K} \in \mathbb{R}^{d_{\text {model }} \times d_{k}}, W_{i}^{V} \in \mathbb{R}^{d_{\text {model }} \times d_{v}}, W^{O} \in \mathbb{R}^{\hat{h} d_{v} \times d_{\text {model }}}$
이 논문에서는 $h=8$ 으로 진행을 하였고 $d_{k}=d_{v}=d_{model}/h=64$ 로 진행을 하였다.
dim을 줄임으로써 multi-head로 늘어난 계산량을 줄이기 위함이다.

3.2.3 Applications of Attention in our Model

transformer에서는 3곳에 multi-head attention을 사용하였다.

encoder-decoder 연결하는 곳에는 Query는 decoder의 이전 layer에서 들어오고 Key, Value는 encoder의 출력 값에서 가져온다. 이를 통해 decoder의 모든 위치에 encoder의 모든 값을 활용할 수 있게 해준다.
encoder 자체에도 multi-head attention이 존재한다. query, key, value는 같은 곳에서 가져오는데 여기에서는 encoder의 이전 layer의 output이다. 이를 통해 encoder도 encoder의 이전 layer의 값을 다 활용할 수 있다.
decoder 자체에서도 사용되는데 여기에서 중요한 점은 기본적인 동작 방식은 encoder와 같지만 decoder에서는 masking이 사용되었다.
만약 masking이 사용되지 않으면 decoder에서는 학습하는 과정에서 이후에 나올 단어들을 미리 볼 수 있게 되고 이는 auto regressing을 방해하기 때문이다. 이를 위해 scaled dot attention을 진행할 때 특정 유사도를 $-\infty$ 로 설정해서 softmax 유사도를 0으로 만드는 방식으로 masking을 진행한다.

3.3 Position-wise Feed-Forward Networks

각 encoder, decoder에서는 linear layer가 존재하는데 이는 2개의 linear layer 사이에 ReLU가 있는 식으로 구성되어있다. 식으로 표현하면 다음과 같다.
$\operatorname{FFN}(x)=\max \left(0, x W_{1}+b_{1}\right) W_{2}+b_{2}$
이는 2개의 1x1 conv layer로도 표현이 가능하다.
입력과 출력의 차원은 $d_{model}=512$ 이고 내부 차원은 $d_{ff}=2048$ 이다.

3.4 Embeddings and Softmax

다른 문장 변환 모델과 비슷하게 transformer 역시 학습된 embedding으로 input token과 output token을 $d_{model}$ 차원 vector로 변환한다. 그리고 decoder에서 liner layer, softmax를 이용해서 다음 토큰의 예측 확률을 계산한다.
이 모델에서는 input, output의 embedding을 만드는 linear layer와 softmax를 공유한다.

3.5 Positional Encoding

transformer는 recurrence, convolution layer가 없기 때문에 model이 문장의 순서를 알아내기 힘들다. 문장이 그냥 그대로 바로 들어가기 때문이다.

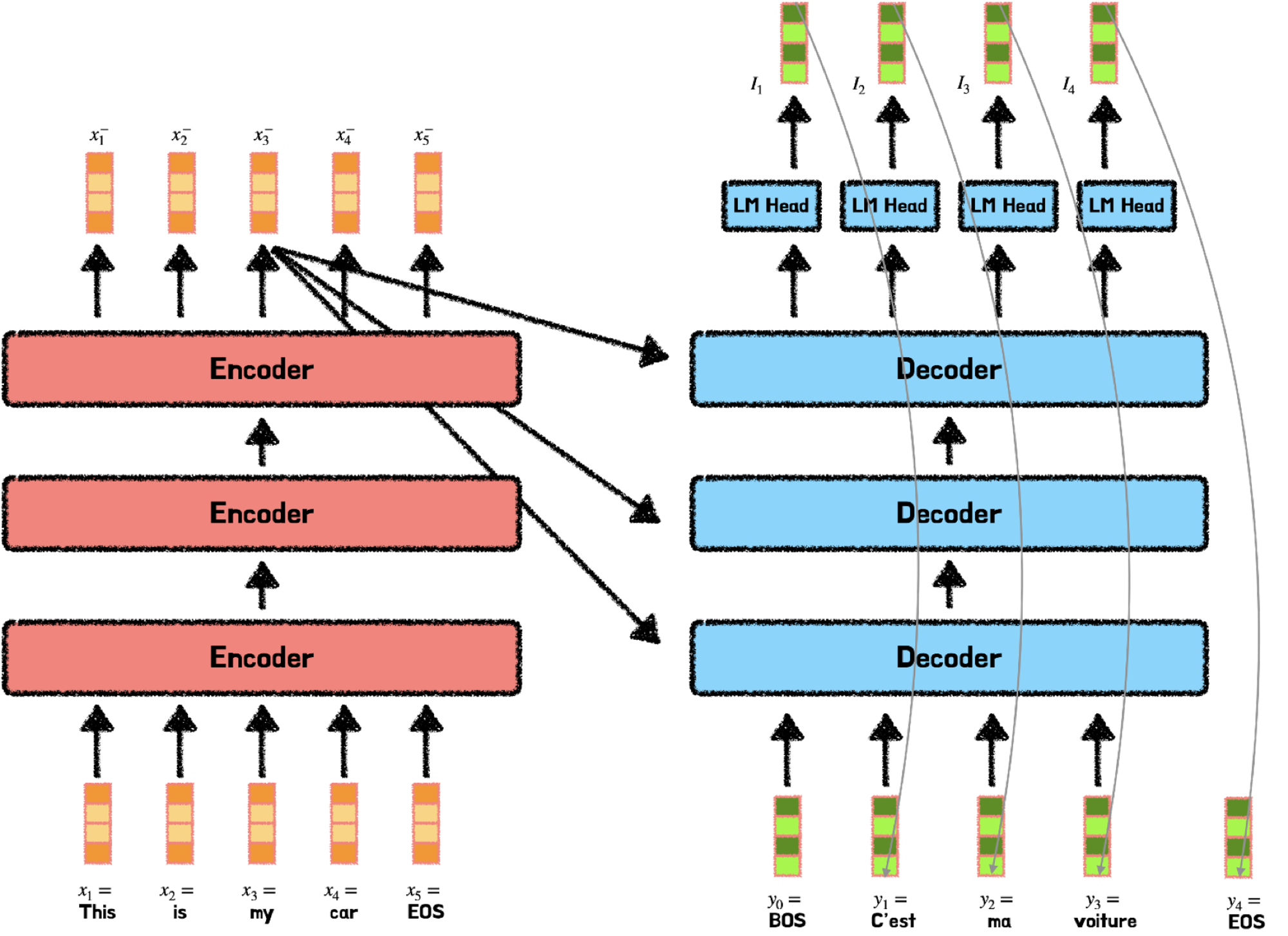
출처
위 그림과 같이 RNN처럼 input이 순차적으로 들어오는게 아니라 바로 병렬적으로 들어온다. 그렇기 때문에 input의 단어 순서를 알기가 어렵다.
(위 그림에서는 $d_{model}=512$ 가 아니라 $d_{model}=4$ 로 표현이 되었다.)

input의 순서가 중요한 이유는

출처
이와 같이 문장의 순서에 따라서 결과가 완전히 바뀔 수 있기 때문이다.

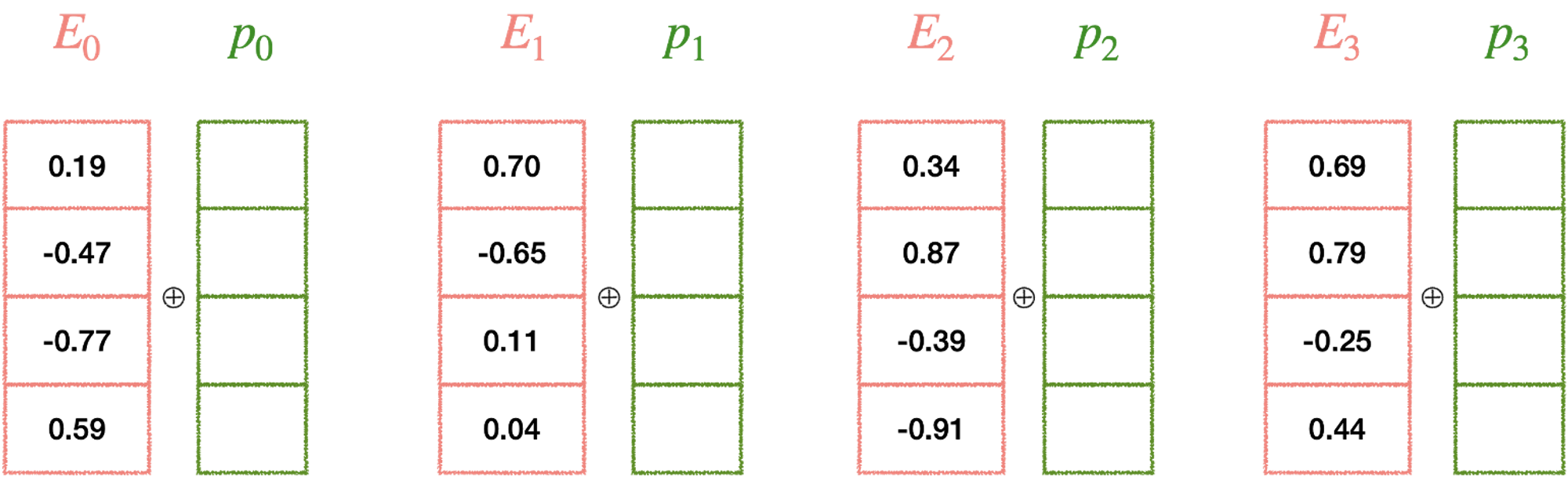
출처
이를 해결하기 위해 위와 같이 position embedding을 추가를 해줘서 각각 어느 순서로 input이 들어왔는지 알 수 있게 해주었다.

그렇다면 어떻게 positional embedding을 더해주었을까?
positinal embedding에서 중요한 조건은 2가지이다.

1. 길이가 변하여도 각 단어 위치를 동일하게 표현할 수 있다.
2. 값이 너무 커서 위치 정보량이 너무 커지면 안된다.

이를 위해 채택된 것이 바로 cos, sin 함수이다.
주기함수이고 값이 -1~1 사이로 적절하기 때문이다.
그러나 여기에서 cos, sin을 함께 사용하는 이유는 주기 함수라는 특성 때문에

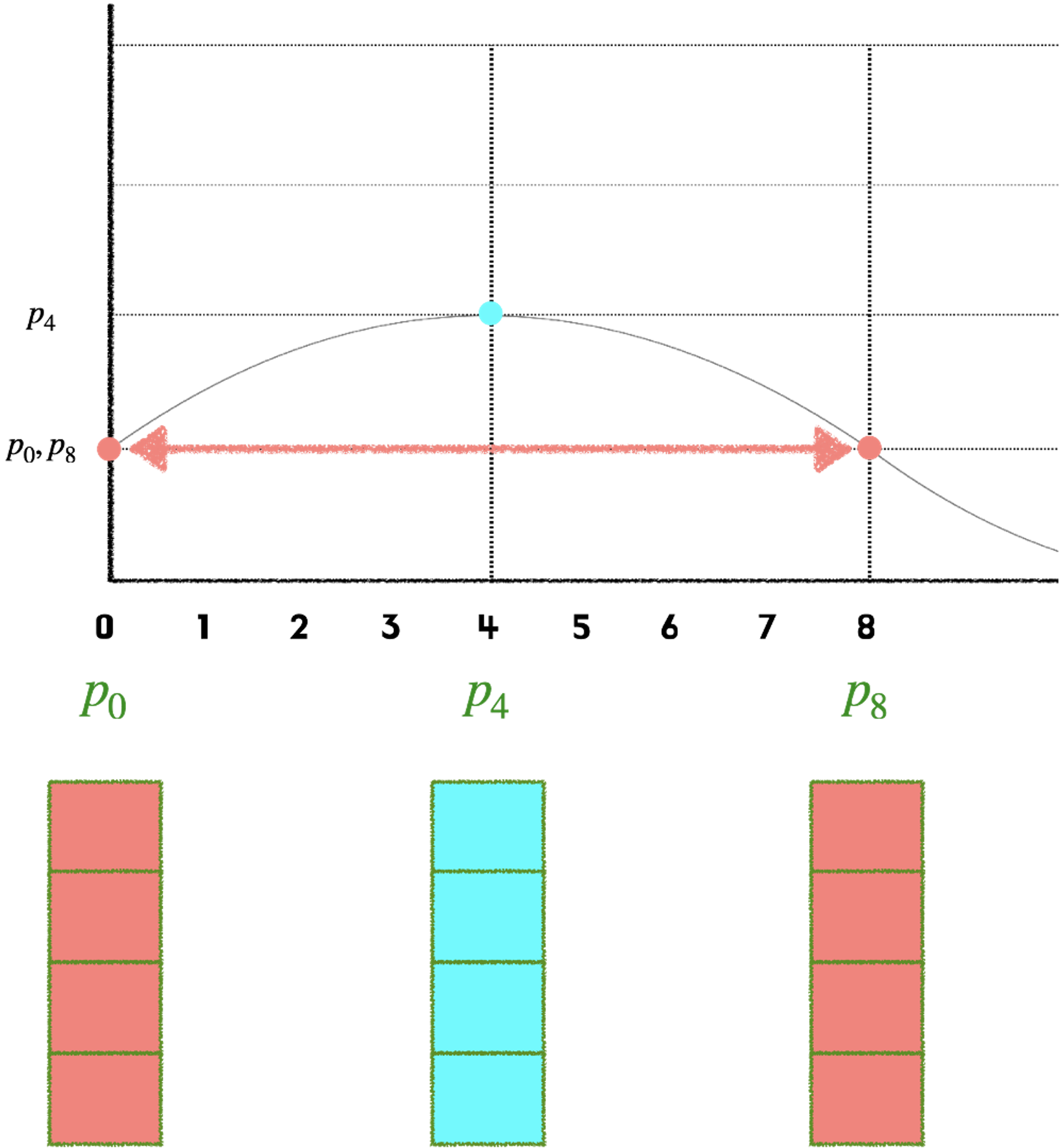
출처
하나만 사용하게 된다면 그림과 같이 같은 값을 가지는 부분이 나올 수 있기 때문이다.
그렇기 때문에 positional embedding이 가진 vector 값이라는 특성을 활용해 position과 vector의 index를 각각 embedding 처리를 한다.
수식은 다음과 같다.
$\begin{aligned} P E_{(p o s, 2 i)} & =\sin \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \\ P E_{(p o s, 2 i+1)} & =\cos \left(p o s / 10000^{2 i / d_{\text {model }}}\right) \end{aligned}$
pos는 단어의 위치이고 i는 vector의 index이다.
각각 vector의 index에 따라서 홀수 짝수를 나누어서 할당해주고 주기가 2pi부터 10000*2pi 까지 변한다.
이를 통해서 겹치는 주기가 거의 발생하지 않게 만들어준다.

4. Why Self-Attention

self attention layer가 convolution이나 recurrent보다 더 좋은 3가지 비교가 제시된다.
1. layer의 계산 비용
2. 병렬화가 가능한 계산량 즉 순차적인 연산량 요구의 최소치 측정
3. network의 long range dependency의 path 길이 dependency를 잘 학습하려면 network에서 forward, backward로 진행이 되는 과정에서 이러한 path가 짧을 수록 dependency를 더 잘 학습한다. 그렇기 때문에 layer의 path 길이도 비교한다.

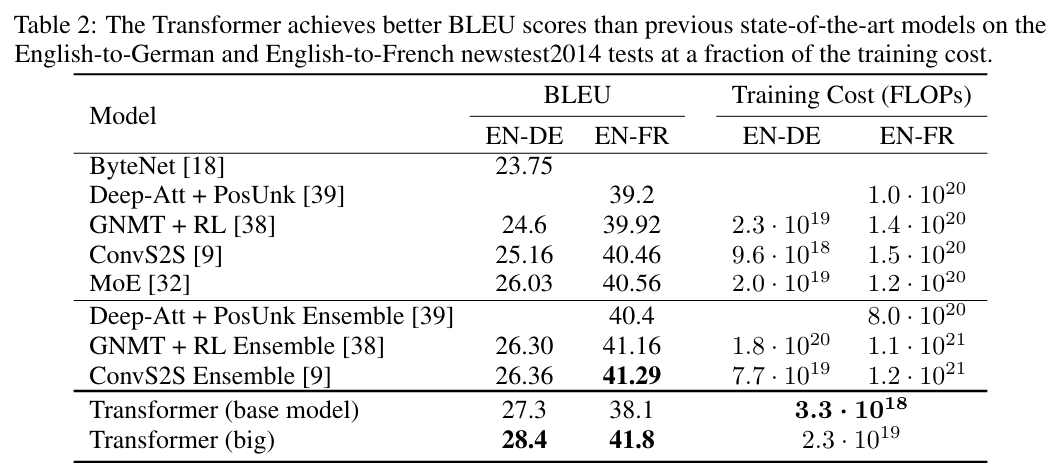
위 테이블의 결과에 따르면 sequential 연산에서 self-attention은 O(1)으로 recurrent 보다 더 좋다.
또한 Maximum path Length의 측면에서도 O(1)으로 매우 좋은 모습을 보여준다.
계산량의 측면에서는 Self-attention은 sequential의 길이 n이 d보다 작을 때 더욱 좋은 모습을 보여준다. 이는 대부분의 상황에서 적용된다.

conclusion

transformer 구조를 통해 attention을 사용하여 주어진 문장의 상관관계를 파악 함으로써 모델이 단어의 문맥을 파악할 수 있게 되었고 이는 번역 에서 적은 비용의 학습으로 매우 좋은 성과를 내었다.

구현

transformer는 이미 pytorch에 구현이 되어있어서
scaled dot-product attention과
multi head attention을 직접 구현해보았다.

class scaled_dot_product_attention(nn.Module):
    def __init__(self):
        super().__init__()

    def forward(self, Q, K, V, mask=None):
        # Q, K, V shape: (batch, num_head, seq_len, d_model//num_head)
        
        d_k = Q.size(-1)
        attn = torch.matmul(Q, K.transpose(-2, -1)) / (d_k**0.5)
        #shape: (batch, num_head, seq_len, seq_len)

        if mask is not None:
            attn[mask == 0] = -1e9
        softmax_attn = F.softmax(attn, dim=-1)
        #shape: (batch, num_head, seq_len, seq_len)
        output = torch.matmul(softmax_attn, V)
        #shape: (batch, num_head, seq_len, d_model//num_head)
        return output


class multi_head_Attention(nn.Module):
    def __init__(self, d_model=512, num_head=8, dropout=0.1):
        super().__init__()
        self.d_model = d_model
        self.d_k=d_model//num_head
        self.num_head = num_head
        self.dropout = nn.Dropout(dropout)
        self.Q = nn.Linear(d_model, d_model)
        self.K = nn.Linear(d_model, d_model)
        self.V = nn.Linear(d_model, d_model)
        self.scaled_dot_product_attention = scaled_dot_product_attention()
        self.out = nn.Linear(d_model, d_model)

    def forward(self, x):
        # x shape: (batch, seq_len, d_model)
        Q = self.Q(x)
        K = self.K(x)
        V = self.V(x)
        # Q, K, V shape: (batch, seq_len, d_model)
        # change into (batch, num_head, seq_len, d_model//num_head)
        Q=Q.view(Q.size(0), Q.size(1), -1, self.d_k).transpose(1, 2)
        K=K.view(K.size(0), K.size(1), -1, self.d_k).transpose(1, 2)
        V=V.view(V.size(0), V.size(1), -1, self.d_k).transpose(1, 2)
        # Q, K, V shape: (batch, num_head, seq_len, d_model//num_head)
        output = self.scaled_dot_product_attention(Q, K, V)
        # output shape: (batch, num_head, seq_len, d_model//num_head)
        output = output.transpose(1, 2).reshape(x.size(0), -1, self.d_model)
        output = self.out(output)
        return output