VAE, ELBO 설명

Tutorial on Diffusion Models for Imaging and Vision을 읽다가 정리하는 내용

VAE?

VAE는 variational auto encoder으로 기존의 auto encoder의 구조에 variational을 추가한 것이다.
이를 통해서 generative model로 이용할 수 있다.

어떻게 generative model로 이용할 수 있을까?

• 기존의 auto encoder의 구조는 위 그림과 같다.
  그냥 image를 latent로 축소하고 복구하는 과정에서 얻어지는 latent를 이용하는 단순한 구조인데.
  이렇게 되면 문제가 1개의 representation으로 각각 이미지가 압축은 되지만 임의의 latent를 주고 복구하는 생성에 이용할 수는 없다.
  왜냐하면 latent로 압축되는 분포를 모르기 때문.
  그냥 각각의 representation으로 압축이 이루어지기 때문이다.

• 반연에 VAE는 latent에 압축할 때 임의의 mean, var을 가지도록 압축을 진행하고 여기에 noise를 넣어서 복구를 진행한다.
  이를 통해 알아낸 임의의 분포에서 생성한 latent에 넣고 복구하면 생성형 모델이 되는 것이다.

ELBO(evidence of lowebound)

엘보가 흔히 VAE와 같이 나오는데 이게 뭘까?

이에대한 설명을 보려면 우선 용어부터 알아야한다.

용어

• $p(\bm x)$: true data의 분포. image의 분포이다. 사실 우리는 이걸 절대 알수 없다.
  만약 알 수 있으면 이 분포에서 임의로 추출하면 우리가 보는 이미지가 나온다.
  생성을 위한 우리의 목표
• $p(\bm{z})$: latent의 분포. 보통 강제로 gaussian에서 mean=0, var=$I$인 $\mathcal{N}(0,\mathbf{I})$이다.
  왜 가우시안이냐 -> 가우시안에서 linear transform을 통해서 어떤 분포든지 만들 수 있기 때문이다. 즉 $p(\bm x)$도 만들 수 있다.
• $p(\bm z| \bm x)$: encoder의 분포. $\bm x$가 주어졌을 때의 $\bm z$의 분포이다. 우리가 간섭할 수 없다. 우리는 이를 network를 이용해서 $q_\phi(\bm z| \bm x)$로 근사해서 표현한다.
• $p(\bm x| \bm z)$: decoder의 분포. $\bm z$가 주어졌을 때의 $\bm x$의 분포이다. 우리가 간섭할 수 없다. 우리는 이를 network를 이용해서 $p_\theta(\bm x| \bm z)$로 근사해서 표현한다.

network를 이용한 근사는 다음과 같다.

• network를 이용한 encoder 근사.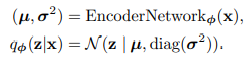간단하게 $\bm \mu, \bm \sigma^2$이 encoder의 output으로 나오고 이 분포를 따르는 $q_\phi(\bm z| \bm x)$로 근사.
• decoder를 이용한 encoder 근사.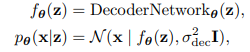encoder와 비슷한데 평균만 network의 output으로 나오고 var은 hyper param이다.

전체구조.

유도

• 수식을 하나씩 적기 힘들어서 사진으로 대체.
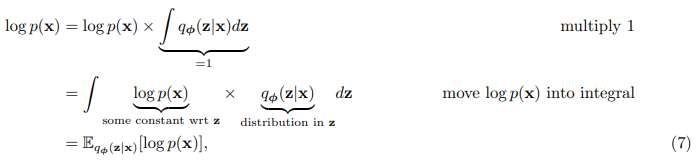  우선 위 수식 간단한 확률과 통계를 알아야 이해가 되는데
  확률에서 기댓값은 $\mathbb{E}[X]=\sum x \cdot f(x)$이다. 즉 값*확률인 것.
  위 식은 적분은 $q_\phi(\bm z| \bm x)$에서 모든 Z에대한 확률을 다 더하면 1이기에 이렇게 푸는 것이 가능하다.
  그래서 위 기댓값 공식에 의해 기댓값으로 표현이 가능하다.
• 이후 bayes 정리를 이용해서 아래와 같이 수식을 전개한다.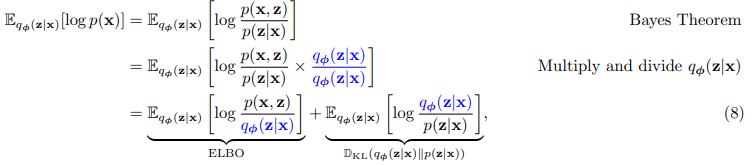여기에서 나오는 $\mathbb{E}_{q_\phi(z|x)}[\log \frac{p(x,z)}{q_\phi(z|x)}]$가 ELBO이다.
  ELBO와 KL을 증가시키면 왼쪽의 decoder가 X를 생성할 수 있는 확률이 커지게 되는데
  이는 우리가 근사로 만든 decoder가 x를 생성할 수 있다는 것을 의미한다

이제 우리의 목표는 ELBO를 높이는 것이다.

ELBO 높이기

그런데 ELBO를 높이기 위해서는 기댓값 내부의 $\log \frac{p(x,z)}{q_\phi(z|x)}$를 높이는 것이 제일 좋은데 문제는 $p(x,z)$는 우리가 모르는 분포이다.
그렇기에 이를 바꿔주는데
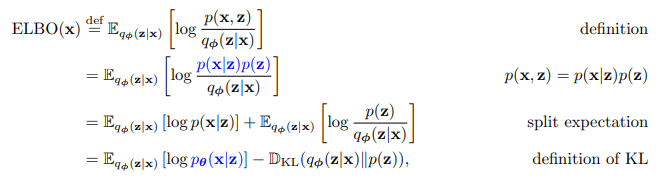위와같은 과정을 거쳐서 ELBO를 우리가 아는 분포들로 바꾼다.
bayse 정리를 사용한 간단한 과정임으로 따로 설명하진 않겠다.
여기에서

• $\mathbb{E}_{q_\phi(z|x)}[\log p_\theta(x|z)]$는 reconstruct term인데 간단하게 $z$로부터 $x$를 복구하는 decoder의 term이고
• $\mathbb{D}_\text{KL}(q_\phi(z|x)||p(z))$는 prior term이다. 이거는 압축되어 만들어지는 분포 $q_\phi(z|x)$가 $p(z)$와 비슷하게 해줌을 의미한다.

optimization

이제 ELBO를 최대화 하기 위해서 optimization을 해줘야하는데 여기에 문제가 있다.
각 param에 따른 미분 값은 위처럼 표현이 가능하고
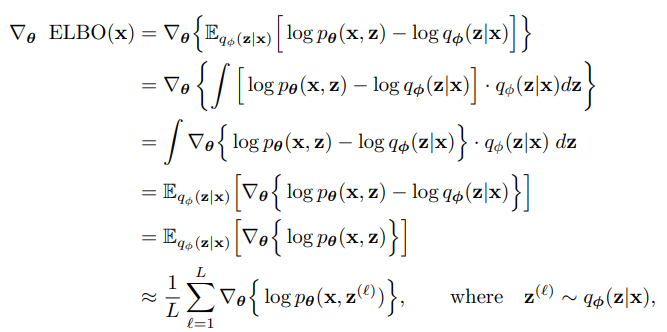이때 decoder $\theta$에 대해서만 미분을 하면 위처럼 딱 떨어진다.
여기에서 중요한 부분은 기댓값의 미분값과 미분값의 기댓값이 동일하다는 것이다.
즉 기댓값의 미분이 미분값의 기댓값이랑 동일하기에 아래와 같이 monte carlo로 gradient를 근사해서 표현할 수 있다.

말이 조금 어려운데 미분한 것의 기댓값이 기댓값 자체를 미분한 것과 동일하다.
여기에서 미분값의 기댓값을 활용한다.
즉 각각 미분을 해서 monte carlo로 더한 것으로 미분 값의 기댓값을 근사할 수 있고 이를 이용해서 ELBO의 미분 값을 찾을 수 있다.
간단하게 여러번 $z$를 뽑아내고 이를 복구하는 학습이 가능하다.

그러나 encoder은 위 식이 성립하지 않는다.
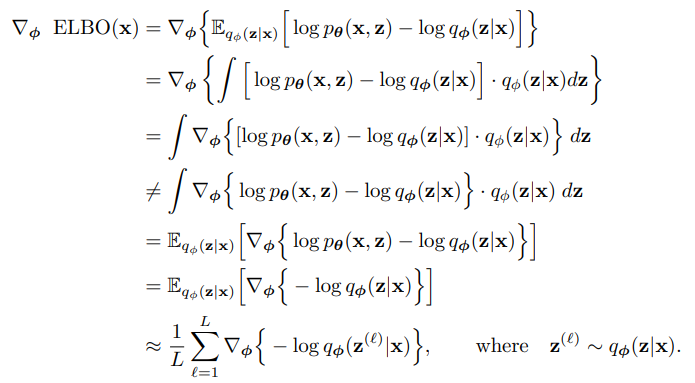위는 encoder $\phi$에 대한 미분인데 여기에서 애초에 분포가 $q_\phi(z|x)$로 encoder을 사용한 분포이기 때문에 이전과 같은 방법으로 미분이 이루어지지 않는다.

reparametrization trick

이를 위해서 trick을 이용하는데 바로 분포를 바꿔주는 것이다.
$q_\phi(z|x)$가 분포에 사용이 되었기에 미분이 안되었다면 이를 바꾸면 되는 것이다.
이를 reparametrization trick이다.

구조는 매우 간단한데 원리는 어렵다.
임의의 $\epsilon \sim \mathcal{N}(0,\mathbf I)$와 $z\sim q_\phi(z|x)=\mathcal{N}(z|\mu,\text{diag}(\sigma^2))$에서
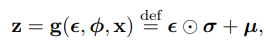위와 같이 $\epsilon$을 std에 곱하고 평균을 더해주는 식으로 $z$를 샘플링하면 된다.

말이 어려운데 pytorch로 생각해보면 쉽다.
encoder가 image를 받아서 평균과 std를 output으로 만든다고 했을 때
여기에서 sampling을 해서 z를 만들고 decoder로 복구하면 decoder은 학습이 되겠지만 encoder는 학습이 이루어지지 않는다.
sampling을 해버리는 부분에서 gradient가 흐르지 않기 때문.

그래서 여기에서 encoder의 output으로 나온 평균과 std를 가지고 reparametrization을 해준다. 그러면 encoder의 output이 그대로 곱셈, 덧셈 연산으로 들어가기 때문에 gradient가 흐를 수 있고 학습이 이루어진다.

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)   # 표준편차
        eps = torch.randn_like(std)     # 표준 정규 분포에서 샘플링
        return mu + eps * std

조금 어려운데 수식적으로 설명을 해보면
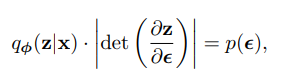위 수식이 성립하기 때문인데 왜 성립하냐면
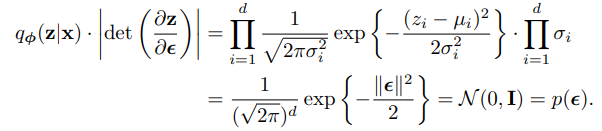위와 같은 과정을 따른다. $q_\phi(z|x)$는 앞의 곱셈 부분인데 위에 적었다시피 $z\sim q_\phi(z|x)=\mathcal{N}(z|\mu,\text{diag}(\sigma^2))$로 정규분포를 따르기 때문에 위와 같이 표현이 가능하고
오른쪽의 sigma 곱셈은 $z$를 $\epsilon$으로 미분하면 각각 element wise로 곱해지는 sigma만 대각선에 있기 때문에 determinant는 sigma의 곱이다.
그렇기에 위와 같이 유도가 된다.

이를 이용하면 위와 같이 encoder에 대한 기댓값을 다른 epsilon에 대한 기댓값으로 근사표현이 가능하고
우리는 이를 미분할 수 있다.

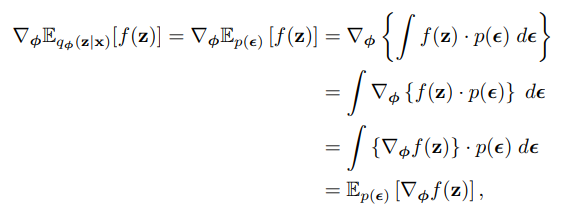
정리

VAE를 학습하기 위해서는 ELBO를 증가시켜야 하고 ELBO를 증가시키면 기존의 encoder, decoder 분포를 잘 근사할 수 있기 때문에 모델을 추론할 수 있다.
그리고 임의의 $z\sim \mathcal{N}(0, I)$에서 sampling한 z를 이용해서 임의의 image를 생성할 수 있다.

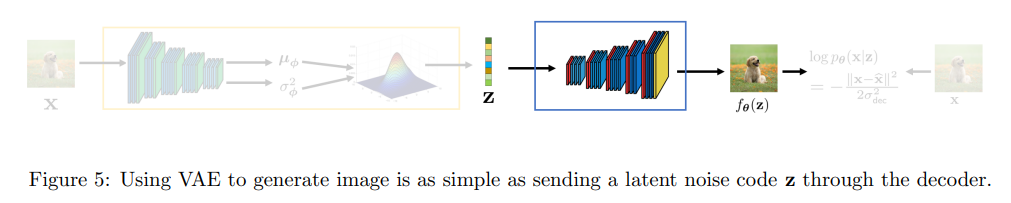위 그림은 전체 학습 구조이고 학습이 완료되면 decoder 부분만 가져와서 사용한다.